KNN算法（k近邻算法）_什么是kn算法

目录

一、KNN算法的概述

二、KNN的核心思想

三、KNN的优缺点

四、数据集内容

五、代码

1、处理数据集

2、knn算法框架

欧氏距离

3、输出结果

六、小结

一、KNN算法的概述

k 近邻法 (k-nearest neighbor, k-NN） 是一种基本分类与回归方法。KNN（K-Nearest Neighbor）算法是机器学习算法中最基础、最简单的算法之一。它既能用于分类，也能用于回归。KNN通过测量不同特征值之间的距离来进行分类。

KNN算法没有一般意义上的学习过程。它的工作原理是利用训练数据对特征向量空间进行划分，并将划分结果作为最终算法模型。存在一个样本数据集合，也称作训练样本集，并且样本集中的每个数据都存在标签，即知道样本集中每一数据与所属分类的对应关系。

二、KNN的核心思想

KNN据有三个基本要素：k 值的选择、距离度量及分类决策规则。

        1. k 值的选择

        一般而言，我们只选择样本数据集中前k个最相似的数据，这就是KNN算法中K的由来，通常k是不大于20的整数。最后，选择k个最相似数据中出现次数最多的类别，作为新数据的分类。

        2. 距离度量

        常用的距离量度方式包括：闵可夫斯基距离、欧氏距离、曼哈顿距离、切比雪夫距离、余弦距离。

三、KNN的优缺点

优点：

1. 简单有效
2. 重新训练的代价低
3. 适合类域交叉样本：KNN方法主要靠周围有限的邻近的样本,而不是靠判别类域的方法来确定所属类别的，因此对于类域的交叉或重叠较多的待分样本集来说，KNN方法较其他方法更为适合。
4. 适合样本容量比较大的类域自动分类：该算法比较适用于样本容量比较大的类域的自动分类，而那些样本容量较小的类域采用这种算法比较容易产生误分。

缺点：

1. 惰性学习：KNN算法是懒散学习方法（lazy learning,基本上不学习），一些积极学习的算法要快很多
2. 类别评分不是规格化：不像一些通过概率评分的分类
3. 输出可解释性不强：例如决策树的输出可解释性就较强
4. 对不均衡的样本不擅长：当样本不平衡时，如一个类的样本容量很大，而其他类样本容量很小时，有可能导致当输入一个新样本时，该样本的K个邻居中大容量类的样本占多数。该算法只计算“最近的”邻居样本，某一类的样本数量很大，那么或者这类样本并不接近目标样本，或者这类样本很靠近目标样本。无论怎样，数量并不能影响运行结果。可以采用权值的方法（和该样本距离小的邻居权值大）来改进。
5. 计算量较大：目前常用的解决方法是事先对已知样本点进行剪辑，事先去除对分类作用不大的样本。

KNN能够快速高效地解决建立在特殊数据集上的预测分类问题，但其不产生模型，因此算法准确 性并不具备强可推广性。

四、数据集内容

Iris数据集里一共包括150行记录，其中前四列为花萼长度，花萼宽度，花瓣长度，花瓣宽度等4个用于识别的属性，鸢尾花第5列为鸢尾花的类别（包括Setosa，Versicolour，Virginica三类）。

通过判定四个尺寸大小识别类别花朵类别，可通过以下网站下载数据集。

UCI Machine Learning Repository

五、代码

1、处理数据集

import numpy as np
import matplotlib.pyplot as plt
from sklearn import svm
from sklearn.preprocessing import label_binarize
from sklearn.metrics import precision_recall_curve,average_precision_score
from sklearn.multiclass import OneVsRestClassifier
 
#切分数据集
from sklearn.model_selection import train_test_split
 
 
filename = "iris copy.txt"
#打开文件
fr = open(filename)
#读取文件所有内容
arrayOLines = fr.readlines()
#得到文件行数
numberOfLines = len(arrayOLines)
#返回的NumPy矩阵,解析完成的数据:numberOfLines行,3列
returnMat = np.zeros((numberOfLines,4))
#返回的分类标签向量
classLabelVector = []
#行的索引值
index = 0
for line in arrayOLines:
    #s.strip(rm)，当rm空时,默认删除空白符(包括'/n','/r','/t',' ')
    line = line.strip()
    #使用s.split(str="",num=string,cout(str))将字符串根据'/t'分隔符进行切片。
    listFromLine = line.split(' ')
    #将数据1-4列提取出来,存放到returnMat的NumPy矩阵中,也就是特征矩阵
    returnMat[index,:] = listFromLine[1:5]
    #根据文本中标记的喜欢的程度进行分类,1代表setosa,2代表versicolor,3代表virginica
    if listFromLine[-1] == '"setosa"':
        classLabelVector.append(1)
    elif listFromLine[-1] == '"versicolor"':
        classLabelVector.append(2)
    elif listFromLine[-1] == '"virginica"':
        classLabelVector.append(3)
    index += 1
#iris = load_iris()
#1-4列为特征，最后一列为标签
 
#划分特征和标签
y=classLabelVector
X=returnMat
#print(y)
#转化为类别标签
y=label_binarize(y,classes=[1,2,3])#标签二值化  y从第一列开始取所以初始值为1
n_classes=y.shape[1]
#print(y)
 
#增加噪声
random_state=np.random.RandomState(0)
n_samples,n_features=X.shape
#在原始x的列上n_feature*n倍级噪声增加n倍
X=np.c_[X,random_state.randn(n_samples,200*n_features)]

2、knn算法框架

欧氏距离

​

def classify0(inX, dataSet, labels, k):
    rows = dataSet.shape[0]  # 计算有多少组特征值
 
    # Step 1: 计算待预测样本与训练数据集中样本特征之间的欧式距离
    diff = np.tile(inX, (rows, 1)) - dataSet # tile作用：将pred_data重复rows次
    sqrt_dist = np.sum(diff**2, axis=1)  # 按行相加，不保持其二维特性
    distance = sqrt_dist ** 0.5 #开方
 
    # Step 2: 按照距离递增的顺序排序
    sorted_indices = np.argsort(distance)
 
    # Step 3: 选取距离最近的K个样本以及所属类别的次数
    map_label = {}
    for i in range(k):
        label = labels[sorted_indices[i]][0]
        map_label[label] = map_label.get(label, 0) + 1
 
    # Step 4: 返回前k个点所出现频率最高的类别作为预测分类结果
    max_num = 0
    for key, value in map_label.items():
        if value > max_num:
            max_num = value
            ans = key
    return ans

3、输出结果

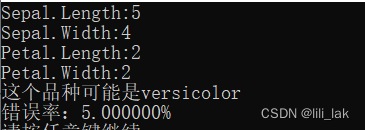
六、小结

学习了KNN算法和部分距离公式的使用。