图论最短路径以及floyd算法的MATLAB实现

图论是数学的一个分支，起源于18世纪。1736年，数学家欧拉通过解决“哥尼斯堡七桥问题”，将问题抽象成点和线的关系，并通过理论分析得出结论，这个过程标志着图论的产生，欧拉也因此被称为“图论之父”。图论研究的是由若干给定的点及连接两点的线所构成的图形，这种图形通常用来描述某些事物之间的某种特定关系，其中点代表事物，连接两点的线表示相应两个事物间具有这种关系。

一、无向图和有向图在图论中都是重要的概念，它们之间存在显著的区别。

首先，从定义上来看，无向图是一种由节点和边组成的数据结构，边没有方向性，也就是说，如果存在一条边(u, v)，那么从u到v和从v到u都是可以的。这种图通常用来表示双向关系，如社交网络中的友谊关系。而有向图则是一种具有方向性的图，由一组顶点和一组有方向的边组成，每条方向的边都连着一对有序的顶点。在有向图中，如果存在一条边(u, v)，那么只能从u到v，但不一定能从v到u。

此外，从应用角度来看，无向图主要用于表示双向关系，如社交网络、传输网络等，以及用于搜索最短路径等问题。而有向图则更多地用于表示具有方向性的关系，如流程、路径规划等。

二、在图论中，最短路径问题是一个经典问题，它涉及从图中某一顶点（源点）出发，到达另一顶点（终点）的所有路径中，寻找各边权值之和最小的路径，这种路径称为最短路径。

最短路径问题可以分为两类：单源最短路径问题和多源最短路径问题。单源最短路径问题是求单个顶点和其他所有顶点的最短路径，而多源最短路径问题则是求所有顶点相互之间的最短路径。对于最短路径问题，有多种算法可以用来求解，包括但不限于：

1. Dijkstra算法：这是最短路径算法中最常用的一种。它基于贪心策略，通过逐步扩展路径来求解最短路径。算法的基本思想是，从一个起始顶点开始，逐步扩展到其他顶点，每次选择当前路径中距离起始顶点最近的顶点进行扩展，直到扩展到目标顶点或者所有顶点都被扩展完毕。
2. Bellman-Ford算法：这也是另一种常用的最短路径算法。
3. Floyd-Warshall算法：这是一种多源最短路径算法，可以求解图中任意两个顶点之间的最短路径。

以下面问题为例解决问题：

clear;clc;
% 注意Matlab中的图节点要从1开始编号
s = {'v1','v1','v1','v2','v3','v3','v4','v5','v5','v5','v5','v6','v6','v7','v9','v9'}; 
t = {'v2','v3','v4','v5','v2','v4','v6','v4','v6','v7','v8','v5','v7','v8','v5','v8'}; 
weight = [6,3,1,1,2,2,10,6,4,3,6,10,2,4,2,3];
%要做出有向图，只需要将graph改为digraph就行了 
G= digraph(s,t,weight);%有向图
myplot = plot(G,'EdgeLabel',G.Edges.Weight,'LineWidth',2);%图赋给一个变量 
set(gca,'XTick',[],'YTick',[]);
%[p,d] = shortestpath(G,start,end,[‘Method’,algorithm])
% 功能:返回图G中start节点到end节点的最短路径%输入参数:
% (1)G- 输入图 (graph 对象|digraph 对象)
% (2) start 起始的节点% 
% (3) end 目标的节点
% (4)[‘Method’,algorithm]是可选的参数，表示计算最短路径的算法。一般我% 们不用手动设置，默认使用的是“auto”，具体可设置的参数见下一页课件。% 输出参数:
%~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~
% (1)P - 最短路径经过的节点 
% (2)d - 最短距离
[P,d] = shortestpath(G,'v1','v8')%求v1到v8的最短路径和距离

%在图中高亮出最短路径
highlight(myplot,P,'EdgeColor','red')

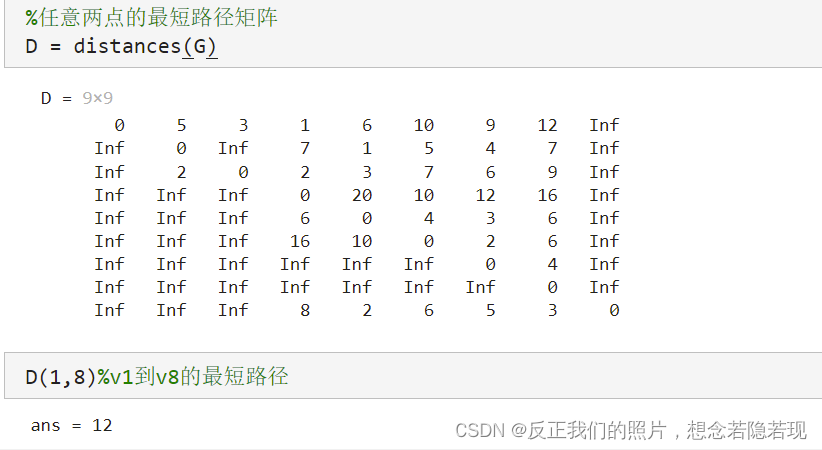
%任意两点的最短路径矩阵
D = distances(G)
D(1,8)%v1到v8的最短路径

下面是代码floyd算法的MATLAB实现：

gg = [0,inf,-2,inf;
      inf,0,inf,-1; 
      inf,2,0,inf;
      4,inf,3,0;];
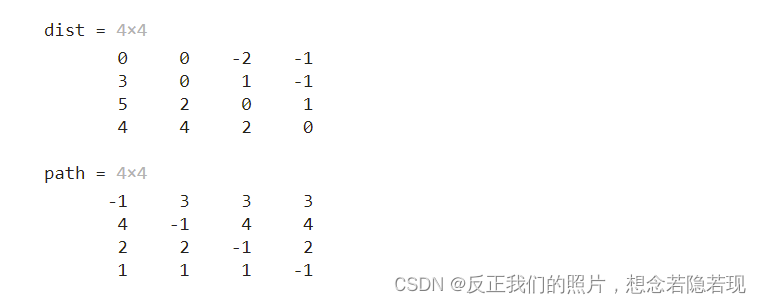
[dist,path] = my_floyd(gg)
function [dist,path] = my_floyd(D)
[r,~]= size(D);
dist = D;
% 下面我们来初始化path矩阵
path = zeros(r);
for j= 1:r
    path(:,j) = j; %将第j列的元素变为j
end
for i = 1:r
    path(i,i) = -1;%将主对角线元素变为-1
end
for k=1:r%以k为中转
    for i=1:r %邻接矩阵第i行
        for j=1:r%邻接矩阵第j列
            if dist(i,j)>dist(i,k)+dist(k,j)
                dist(i,j)=dist(i,k)+dist(k,j);
                path(i,j)=path(i,k);
                % 起点为i，终点为j的两个节点之间的最短路径要经过的节点更新为path(i,k)
                % 注意，上面一行语句不能写成path(i,j) = k;
            end
        end
    end
end
end

 总的来说，图论是一门研究图与网络的理论学科，它在各个领域都发挥着重要的作用，为解决实际问题提供了有力的工具和方法。