LFM回波信号仿真，加汉明窗，可用的matlab代码_利用汉宁窗口反卷积脉冲响应函数 matlab

LFM回波信号仿真，加汉明窗，可用的matlab代码

运行结果（文尾有程序）

在数字信号处理过程中，每次FFT变换只能对有限长度的时域数据进行变换，因此，需要对时域信号进行信号截断。
即使是周期信号，如果截断的时间长度不是周期的整数倍（周期截断），那么，截取后的信号将会存在泄漏。为了将这个泄漏误差减少到最小程度（注意我说是的减少，而不是消除），我们需要使用加权函数，也叫窗函数。

理想频响是分段恒定的，在边界频率处有突变点，所以，这样得到的理想滤波器单位脉冲响应hd(n)是无限长序列，而且是非因果的。但FIR的h(n)是有限长的，怎样用一个有限长的序列去近似无限长的hd(n)？最简单的办法是直接截取一段 hd(n) 代替 h(n) 。这种截取可以形象地想像为h(n)是通过一个“窗口”所看到的一段hd(n)，因此，h(n)也可表达为hd(n)乘以一个“窗函数”

加窗主要是为了使时域信号似乎更好地满足FFT处理的周期性要求，减少泄漏。这里面，有很多窗函数可以使用，不过，每种窗函数的使用场景是不同的。由于直接对信号（加矩形窗）截断会产生频率泄露，为了改善频率泄露的情况，加非矩形窗，一般都是加汉明窗，因为汉明窗的幅频特性是旁瓣衰减较大，主瓣峰值与第一个旁瓣峰值衰减可达40db。

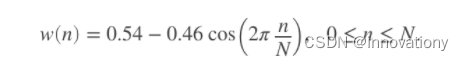
%% Pulse Compress
clear all; close all; clc;

% LFM parameter
B       =   4e+6;       % 4MHz带宽
Tao     =   200e-6;     % 200us时宽
T       =   2e-3;       % 2ms脉冲重复周期 
fs      =   8e+6;       %采样频率
SNR     =   20;         % 信噪比20dB
dis     =   T*fs/2;     % 将目标设置在回波中间处

% Generate LFM
t = -round(Tao*fs/2):1:round(Tao*fs/2)-1; % 脉冲采样点 
lfm = (10^(SNR/20))*exp(1i*pi*B/Tao*(t/fs).^2);

figure;
subplot(2,1,1); plot(real(lfm),'b'); title('线性调频信号实部');
subplot(2,1,2); plot(imag(lfm),'r'); title('线性调频信号虚部');

% Generate echo
echo  = zeros(1,T*fs);
echo(dis:1:dis+Tao*fs-1) = lfm;
noise = normrnd(0,1,1,T*fs) + 1i*normrnd(0,1,1,T*fs);
echo = echo + noise;

figure;
subplot(2,1,1); plot(real(echo),'b'); title('回波信号实部');
subplot(2,1,2); plot(imag(echo),'r'); title('回波信号虚部');

% Generate filter coeff
coeff = conj(fliplr(lfm)).* hamming(Tao*fs).'; %翻转共轭/加汉明窗

figure; freqz(coeff);

% pulse compress
fft_n = 2^(floor(log2(T*fs)) + 1);
pc_res = ifft(fft(echo,fft_n).*fft(coeff,fft_n)); % 未截取不完全滤波点

figure;
plot(db(abs(pc_res)/max(abs(pc_res))),'r');  title('脉压结果分贝图');
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40