红黑树（RBTree）

红黑树（RBTree）

什么是红黑树？

红黑树是在1972年由Rudolf Bayer发明的，当时被称为平衡二叉B树（symmetric binary B-trees）.

在1978年被 Leo J. Guibas 和 Robert Sedgewick 修改为如今的“红黑树”.

红黑树也是一种自平衡二叉查找树，它与AVL树类似，都在添加和删除的时候通过旋转操作保持二叉树的平衡，以求更高效的查询性能。

与AVL树相比，红黑树牺牲了部分平衡性，以换取插入/删除操作时较少的旋转操作，整体来说性能要优于AVL树。

虽然RBTree是复杂的, 但它的最坏情况运行时间也是非常良好的,并且在实践中是高效的：

它可以在O(log n)时间内做查找,插入和删除,这里的n 是树中元素的数目.

红黑树的特性

红黑树是实际应用中最常用的平衡二叉查找树，它不严格的具有平衡属性，但平均的使用性能非常良好。

在红黑树中，节点被标记为红色和黑色两种颜色。

红黑树的原则有以下几点：
特性1：节点非黑即红
特性2：根节点一定是黑色
特性3：叶子节点（NIL）一定是黑色
特性4：每个红色节点的两个子节点都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
特性5：从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点。

红色属性说明，红色节点的孩子，一定是黑色。 但是，RBTree 黑色节点的孩子，可以是红色，也可以是黑色。

叶子属性说明， 叶子节点可以是空nil ，AVL的叶子节点不是空的

基于上面的原则，我们一般在插入红黑树节点的时候，会将这个节点设置为红色，

**原因：**参照最后一条原则： 红色破坏原则的可能性最小，如果是黑色, 很可能导致这条支路的黑色节点比其它支路的要多1，破坏了平衡。

记忆要点：
可以按照括号里边的分类，记住红黑树的几个原则：
（颜色属性）性质1：节点非黑即红
（根属性）性质2：根节点一定是黑色
（叶子属性）性质3：叶子节点（NIL）一定是黑色
（红色属性）性质4：每个红色节点的两个子节点，都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
（黑色属性）性质5：从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点。

黑色属性，可以理解为平衡特征，如果满足不了平衡特征，就要进行平衡操作。

空间换时间
RBT有点属于一种空间换时间类型的优化，在avl的节点上，增加了颜色属性的数据，相当于增加了空间的消耗。 通过颜色属性的增加，换取，后面平衡操作的次数减少。

黑色完美平衡

红黑树并不是一颗AVL平衡二叉搜索树，从图上可以看到，根节点P的左子树显然比右子树高

根据红黑树的特性5，从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点，说明：
rbt 的左子树和右子树的黑节点的层数是相等的
红黑树的平衡条件，不是以整体的高度来约束的，而是以黑色节点的高度，来约束的。
所以称红黑树这种平衡为黑色完美平衡。

看看黑色完美平衡的效果，
去掉 rbt中的红色节点，会得到一个四叉树， 从根节点到每一个叶子，高度相同，就是rbt的root到叶子的黑色路径长度

红黑树的恢复平衡过程的三个操作

一旦红黑树5个原则有不满足的情况，我们视为平衡被打破，如何恢复平衡？ 靠它的三种操作：变色、左旋、右旋。

变色

节点的颜色由红变黑或由黑变红。

左旋

以某个结点作为支点(pivot)，其父节点（子树的root）旋转为自己的左子树（左旋），pivot的原左子树变成 原root节点的右子树，pivot的原右子树保持不变。

右旋：

以某个结点作为支点(pivot)，其父节点（子树的root）旋转为自己的右子树（右旋），pivot的原右子树变成 原root节点的左子树，pivot的原左子树保持不变。

红黑树的左旋、右旋操作，AVL树的左旋，右旋操作 差不多

红黑树节点插入

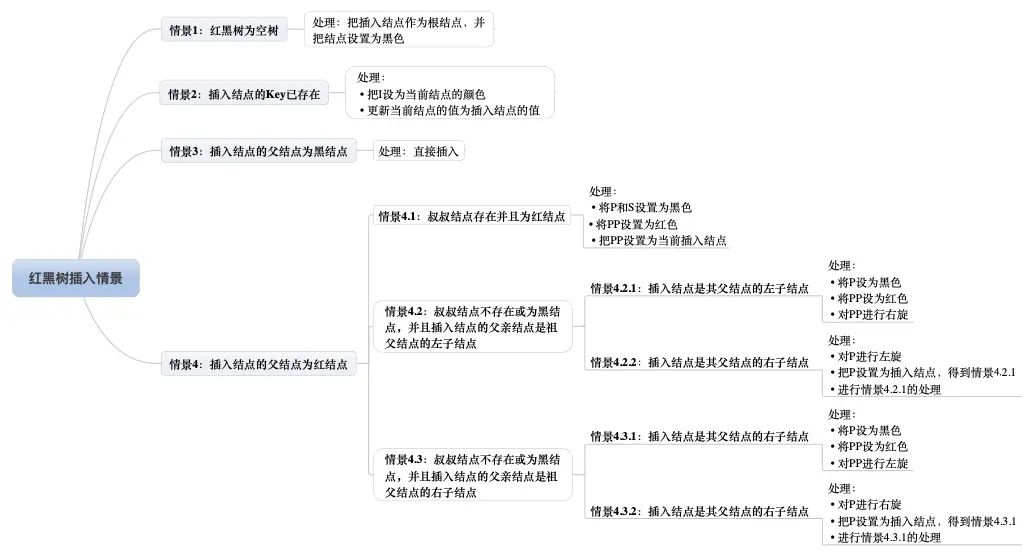
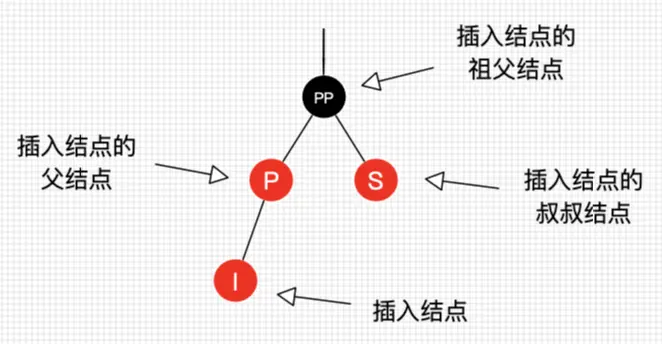
默认新插入的节点为红色：
因为父节点为黑色的概率较大，插入新节点为红色，可以避免颜色冲突

场景1：红黑树为空树

直接把插入结点作为根节点就可以了

另外：根据红黑树性质 2根节点是黑色的。还需要把插入节点设置为黑色。

场景2：插入节点的Key已经存在

更新当前节点的值，为插入节点的值。

情景3：插入节点的父节点为黑色

由于插入的节点是红色的，当插入节点的父节点是黑色时，不会影响红黑树的平衡.所以直接插入无需做自平衡。

情景4：插入节点的父节点为红色

根据性质2：根节点是黑色。
如果插入节点的父节点为红色节点，那么该父节点不可能为根节点，所以插入节点总是存在祖父节点(三代关系)。

根据性质4：每个红色节点的两个子节点一定是黑色的。不能有两个红色节点相连。

此时会出现两种状态：
父亲和叔叔为红色
父亲为红色，叔叔为黑色

场景4.1：父亲和叔叔为红色节点

根据性质4：红色节点不能相连 ==》祖父节点肯定为黑色节点：
父亲为红色，那么此时该插入子树的红黑树层数的情况是：黑红红。

因为不可能同时存在两个相连的红色节点，需要进行变色

变色处理：==黑红红 > 红黑红

1. 将F和V节点改为黑色
2. 将P改为红色
3. 将P设置为当前节点，进行后续处理
   

可以看到，将P设置为红色了，
如果P的父节点是黑色，那么无需做处理；
但如果P的父节点是红色，则违反红黑树性质了，所以需要将P设置为当前节点，继续插入操作, 作自平衡处理，直到整体平衡为止。

场景4.2：叔叔为黑色，父亲为红色，并且插在父亲的左节点

叔叔为黑色，或者不存在（NIL)也是黑节点，并且节点的父亲节点是祖父节点的左子节点
注意：单纯从插入来看，叔叔节点非红即黑(NIL节点)，否则破坏了红黑树性质5，此时路径会比其他路径多一个黑色节点。

场景4.2.1 LL型失衡

新插入节点，为其父节点的左子节点(LL红色情况)， 插入后 就是LL 型失衡

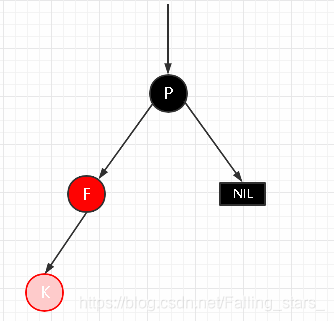
自平衡处理：

1. 变颜色：
   将F设置为黑色，将P设置为红色
2. 对F节点进行右旋
   

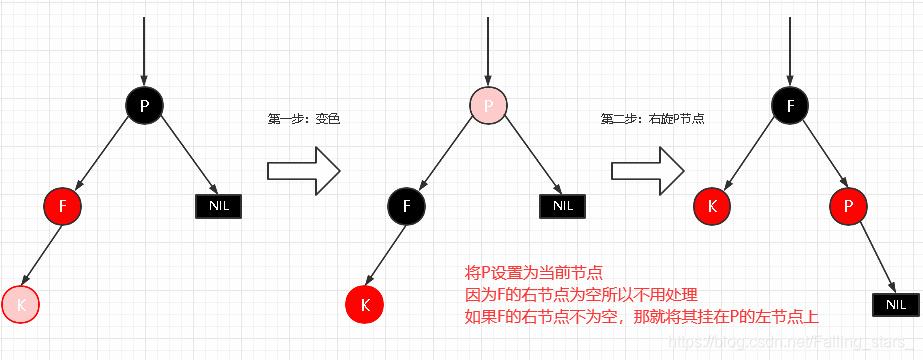
场景4.2.2 LR型失衡

新插入节点，为其父节点的右子节点(LR红色情况)， 插入后 就是LR 型失衡

自平衡处理：

1. 对F进行左旋
2. 将F设置为当前节点，得到LL红色情况
3. 按照LL红色情况处理(1.变色 2.右旋P节点)
   

情景4.3：叔叔为黑节点，父亲为红色，并且父亲节点是祖父节点的右子节点

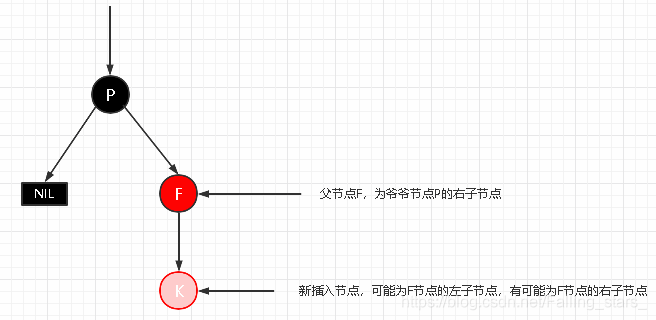
情景4.3.1：RR型失衡

新插入节点，为其父节点的右子节点(RR红色情况)

自平衡处理：

1. 变色：
   将F设置为黑色，将P设置为红色
2. 对P节点进行左旋
   

情景4.3.2：RL型失衡

新插入节点，为其父节点的左子节点(RL红色情况)

自平衡处理：

1. 对F进行右旋
2. 将F设置为当前节点，得到RR红色情况
3. 按照RR红色情况处理(1.变色 2.左旋 P节点)
   

红黑树节点删除

红黑树的删除操作也包括两部分工作：

• 查找目标结点
• 删除后自平衡

不存在目标结点时，忽略本次操作；存在目标结点时，删除后就得做自平衡处理。删除结点后还需要找结点来替代删除结点的位置，不然子树跟父辈结点断开了，除非删除结点刚好没子结点，那么就不需要替代。

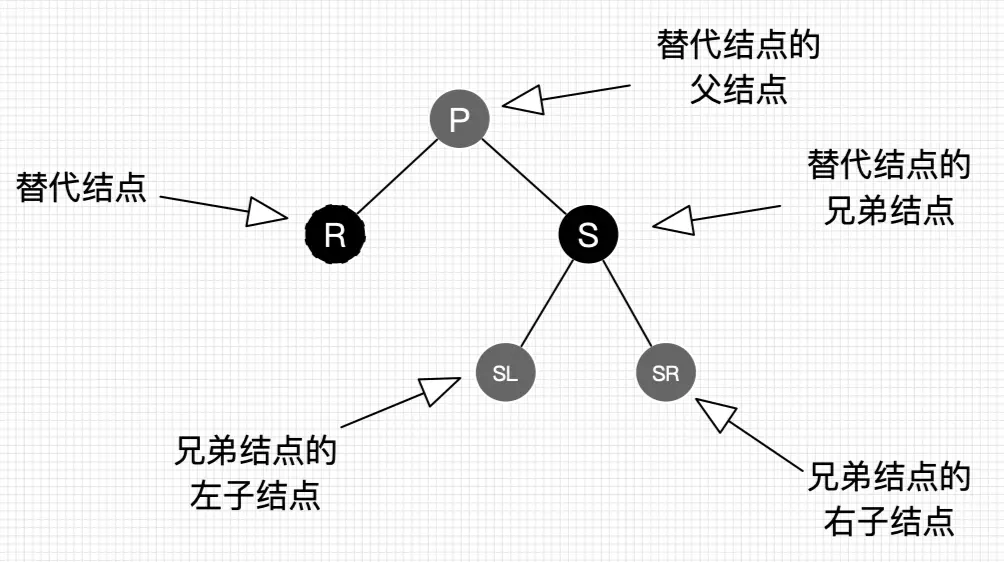
注意：R是即将被替换到删除结点的位置的替代结点，在删除前，它还在原来所在位置参与树的子平衡，平衡后再替换到删除结点的位置，才算删除完成。

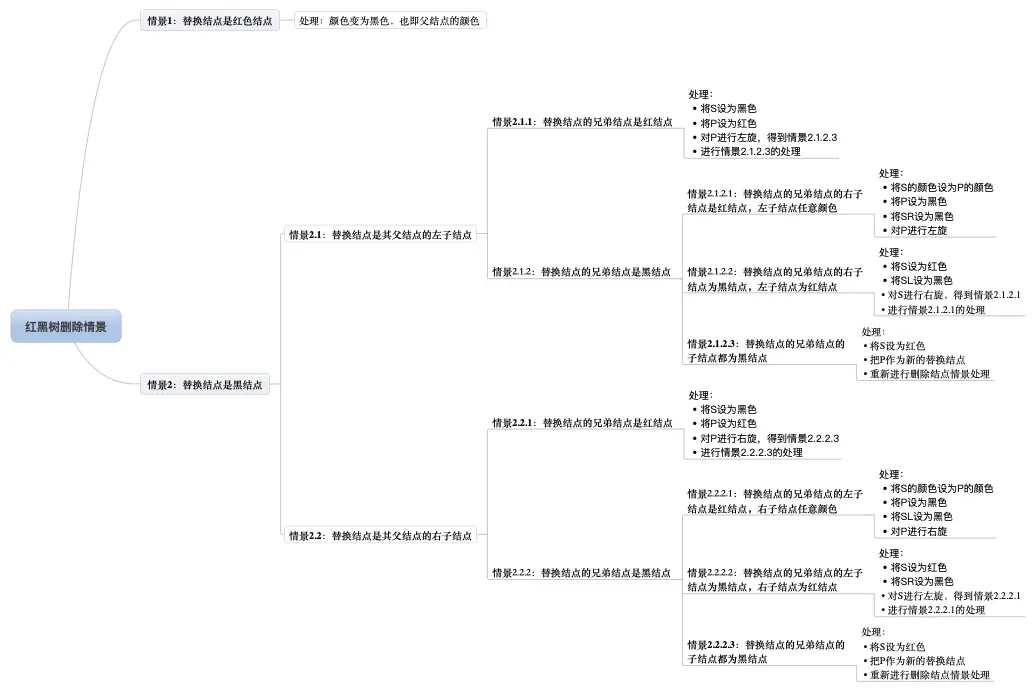
情况1：替换结点是红色结点

把替换结点换到了删除结点的位置时，由于替换结点时红色，删除也了不会影响红黑树的平衡，只要把替换结点的颜色设为删除的结点的颜色即可重新平衡。

处理：颜色变为删除结点的颜色

情况2：替换结点是黑结点

当替换结点是黑色时，就得进行自平衡处理。考虑替换结点是其父结点的左子结点还是右子结点，来做不同的旋转操作，使树重新平衡。

情况2.1：替换结点是其父结点的左子结点

情况2.1.1：替换结点的兄弟结点是红结点

若兄弟结点是红结点，根据性质4，兄弟结点的父结点和子结点肯定为黑色。所以
处理：

• 将S设为黑色
• 将P设为红色
• 对P进行左旋，得到情景2.1.2.3
• 进行情况2.1.2.3的处理

情况2.1.2：替换节点的兄弟节点是黑色

兄弟节点为黑，则无法确定父节点和子节点的颜色。

情况2.1.2.1：替换节点的兄弟节点的右子节点是红色，左子节点为任意颜色

替换节点是黑色，删除后左子树少一个黑色节点，那么必须从右子树借一个黑色节点，则必须左旋。
处理：

• 将S的颜色设为P的颜色
• 将P设为黑色
• 将SR设为黑色
• 对P进行左旋
  
  删除R则无影响。

情况2.1.2.2：替换节点的兄弟节点的右子节点为黑色，左子节点为红色。

若删除R则必须从右节点借一个红色节点才能不影响平衡，所以考虑将情况2.1.2.2转换为情况2.1.2.1。
处理：

• 将S设为红色
• 将SL设为黑色
• 对S进行右旋，得到情景2.1.2.1
• 进行情景2.1.2.1的处理
  

情况2.1.2.3：替换节点的兄弟节点的子节点都是黑色

这种情况没有兄弟的红色节点借给你了，所以必须要找别的地方拿红节点，那么由红黑树是自底向上生长的性质我们想到，可以和增加节点一样，将P作为新的替换节点,但是实际删除的还是R。只是把P当作是替换节点去自底向上的重复上述情况处理。

• 将S设为红色
• 把P作为新的替换结点
• 重新进行删除结点情景处理
  处理：
  

情况2.2：替换节点是其父节点的右子节点

同理情况2.1，这是以前继节点作为替换节点进行处理。

情况2.2.1：替换节点的兄弟节点是红色

处理：

• 将S设为黑色
• 将P设为红色
• 对P进行右旋，得到情景2.2.2.3
• 进行情景2.2.2.3的处理
  

情况2.2.2：替换节点的兄弟节点是黑色

情况2.2.2.1：替换节点的兄弟节点的左子节点是红节点，右子节点任意颜色

处理：

• 将S的颜色设为P的颜色
• 将P设为黑色
• 将SL设为黑色
• 对P进行右旋
  

情况2.2.2.2：替换节点的兄弟节点的左子节点为黑色，右子节点为红色

处理：

• 将S设为红色
• 将SR设为黑色
• 对S进行左旋，得到情景2.2.2.1
• 进行情景2.2.2.1的处理
  

情况2.2.2.3：替换节点的兄弟节点的子节点都是黑色

处理：

• 将S设为红色
• 把P作为新的替换结点
• 重新进行删除结点情景处理
  

规律总结

• 循环条件：x != root && x.color = BLACK，x不是根节点且颜色为黑色
• 收尾操作：将x置为黑色
• x为父亲的左儿子或右儿子，处理操作是对称的；同样只需要记住左儿子时的操作，即可举一反三

x为父亲的左儿子

• 兄弟为红色：将兄弟变成黑色，父节点变成红色；对父节点左旋，恢复左子树的黑色高度，左侄子成为新的兄弟
• 兄弟为黑色，左右侄子为黑色：兄弟变成红色，x指向父节点，继续进行调整
• 兄弟为黑色，右侄子为黑色（左侄子为红色）：左侄子变成黑色，兄弟变成红色；兄弟右旋，恢复右子树的黑色高度，左侄子成为新的兄弟
• 兄弟为黑色，右侄子为红色：兄弟变成父节点颜色，父节点和右侄子变成黑色；父节点左旋，x指向整棵树的根节点，结束循环

RBT面试题：

问：有了二叉搜索树，为什么还需要平衡二叉树？

二叉搜索树容易退化成一条链
这时，查找的时间复杂度从O (log n）也将退化成O (N)
引入对左右子树高度差有限制的平衡二叉树AVL，保证查找操作的最坏时间复杂度也为O (log n）

问：有了平衡二叉树，为什么还需要红黑树？

AVL的左右子树高度差不能超过1，每次进行插入/删除操作时，几乎都需要通过旋转操作保持平衡
在频繁进行插入/删除的场景中，频繁的旋转操作使得AVL的性能大打折扣
红黑树通过牺牲严格的平衡，换取插入/删除时少量的旋转操作。

整体性能优于AVL

• 红黑树插入时的不平衡，不超过两次旋转就可以解决；删除时的不平衡，不超过三次旋转就能解决
• 红黑树的红黑规则，保证最坏的情况下，也能在O ( log n）时间内完成查找
  操作

问：红黑树那几个原则，你还记得么？

可以按照括号里边的分类，记住红黑树的几个原则：

• （颜色属性）节点非黑即红
• （根属性）根节点一定是黑色
• （叶子属性）叶子节点（NIL）一定是黑色
• （红色属性）每个红色节点的两个子节点，都为黑色。(从每个叶子到根的所有路径上不能有两个连续的红色节点)
• （黑色属性）从任一节点到其每个叶子的所有路径，都包含相同数目的黑色节点。

问：红黑树的有那些内部操作

变色
把一个红色的节点变成黑色，或者把一个黑色的节点变成红色，就是对这个节点的变色。
旋转
与平衡二叉树的旋转操作类似。

红黑树与AVL树区别

1. 调整平衡的实现机制不同
   红黑树根据路径上黑色节点数目一致，来确定是否失衡，如果失衡，就通过变色和旋转来恢复

AVL根据树的平衡因子(所有节点的左右子树高度差的绝对值不超过1)，来确定是否失衡，如果失衡，就通过旋转来恢复

1. 红黑树的插入效率更高

红黑树是用非严格的平衡来换取增删节点时候旋转次数的降低，任何不平衡都会在三次旋转之内解决，

红黑树并不追求“完全平衡”，它只要求部分地达到平衡要求，降低了对旋转的要求，从而提高了性能

而AVL是严格平衡树(高度平衡的二叉搜索树)，因此在增加或者删除节点的时候，根据不同情况，旋转的次数比红黑树要多。

所以红黑树的插入效率更高

3、红黑树统计性能比AVL树更高
红黑树能够以O(log n) 的时间复杂度进行查询、插入、删除操作。
AVL树查找、插入和删除在平均和最坏情况下都是O(log n)。

红黑树的算法时间复杂度和AVL相同，但统计性能比AVL树更高，

4、适用性：AVL查找效率高
如果你的应用中，查询的次数远远大于插入和删除，那么选择AVL树，如果查询和插入删除次数几乎差不多，应选择红黑树。

即，有时仅为了排序（建立-遍历-删除），不查找或查找次数很少，R-B树合算一些。

红黑树 VS AVL树

常见的平衡树有红黑树和AVL平衡树，为什么STL和linux都使用红黑树作为平衡树的实现？大概有以下几个原因：

1. 从实现细节上来讲，如果插入一个结点引起了树的不平衡，AVL树和红黑树都最多需要2次旋转操作，即两者都是O(1)；但是在删除node引起树的不平衡时，最坏情况下，AVL需要维护从被删node到root这条路径上所有node的平衡性，因此需要旋转的量级O(logN)，而RB-Tree最多只需3次旋转，只需要O(1)的复杂度

2. 从两种平衡树对平衡的要求来讲，AVL的结构相较RB-Tree来说更为平衡，在插入和删除node更容易引起Tree的unbalance，因此在大量数据需要插入或者删除时，AVL需要rebalance的频率会更高。因此，RB-Tree在需要大量插入和删除node的场景下，效率更高。自然，由于AVL高度平衡，因此AVL的search效率更高。

3. 总体来说，RB-tree的统计性能是高于AVL的。