大白话之lora微调_lora微调是什么意思

什么是Lora微调

LoRA（Low-Rank Adaptation）微调是一种用于调整大型预训练模型的高效微调技术。这种方法主要针对如何在保持模型大部分参数固定的同时，通过引入少量可训练参数来调整模型以适应特定任务。

LoRA 微调的关键特点：
1低秩逼近：LoRA 通过在模型的权重矩阵中引入低秩矩阵来实现微调。这些低秩矩阵的秩（即维度）远小于原始权重矩阵的秩，这意味着它们包含的可训练参数数量较少。

2**参数效率：**由于只需要训练少量额外参数，LoRA 微调的计算和存储开销比全参数微调要小得多。这使得它特别适合于资源受限的环境。

3**保持预训练知识：**在 LoRA 微调中，原始模型的大部分参数保持不变，这有助于保持预训练期间学到的知识，同时通过少量参数的调整来适应新任务。

4**灵活性：**LoRA 可以应用于模型的不同层，允许灵活地决定哪些层需要调整以最好地适应特定任务。

什么是低秩矩阵

我们经常搜lora微调得到上述学术性的解答。那么，第一个问题：lora微调中的低秩矩阵是什么呢？

低秩矩阵是指在线性代数中，其秩（即矩阵中线性无关的行或列的最大数目）较低的矩阵。矩阵的秩反映了它所包含的信息的多少和复杂程度。在许多实际应用中，包括机器学习和信号处理，低秩矩阵有着重要的作用。

基本概念：
秩：矩阵的秩是其行或列的最大线性无关集的大小。秩可以被视为矩阵中包含的独立信息的量度。
**低秩：**如果一个矩阵的秩远小于其行数和列数，它就被认为是低秩的。例如，一个100x100的矩阵，如果其秩只有10，那么它就是一个低秩矩阵。

低秩矩阵的特点和应用：
数据压缩：低秩矩阵可以用来有效地压缩数据。如果一个大矩阵可以近似为一个低秩矩阵，那么存储和处理这个矩阵所需的资源就会大大减少。
特征提取：在机器学习和统计分析中，低秩矩阵常用于特征提取和数据降维。例如，主成分分析（PCA）就是一种通过寻找数据的低秩表示来提取关键特征的技术。
噪声过滤：低秩矩阵也常用于噪声过滤和数据恢复。在这些应用中，假设数据的真实结构可以由低秩矩阵表示，而噪声和异常值导致的额外复杂性可以被去除。
图像处理：在图像处理中，低秩矩阵常用于图像去噪、压缩和恢复。
推荐系统：在推荐系统中，低秩矩阵分解技术可以帮助发现用户和物品之间的潜在关系，从而提高推荐的准确性。

数学表示：
从数学的角度来看，任何低秩矩阵都可以通过矩阵分解来表示，例如奇异值分解（SVD）。通过这种分解，原始矩阵可以表示为几个更小的矩阵的乘积，这些小矩阵包含了原始矩阵的主要信息。

举例子

原始数据
首先，假设我们有一个关于学生考试成绩的数据矩阵，其中每一行代表一个学生，每一列代表一门课程的成绩。

假设这个矩阵长这样：

学生 数学 物理 化学
学生 A 90 85 95
学生 B 60 55 65
学生 C 30 25 35
这个矩阵是一个 3×3 矩阵。我们可以观察到，每个学生在三门科目上的成绩是相似的模式：如果他们在数学上得分高，那么在物理和化学上也会得分较高，反之亦然。

LoRA 微调步骤
选择一个基准列：在这个例子中，我们选择“数学”成绩作为基准列。

确定微调参数：我们观察到物理和化学成绩与数学成绩有线性关系。因此，我们引入两组参数：一个用于物理（比如 $a1$和$b1$），另一个用于化学（比如 $a2$和$b2$）。这些参数将用于调整基准列的值以预测其他科目的成绩。

应用微调：我们将使用这些参数来创建一个低秩矩阵，该矩阵将与基准列相乘以生成物理和化学成绩的预测值。例如，物理成绩可以用 $a1\ast 数学成绩+b1$来计算，化学成绩可以用$a2\ast 数学成绩+b2$来计算。

微调后的矩阵
假设经过训练，我们找到了以下参数：$a1=0.95，b1=0，a2=1.05，b2=0$
我们现在可以用这些参数来预测物理和化学成绩：

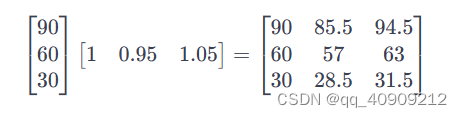
这个矩阵是微调后的结果，它提供了对原始数据的低秩近似。

结论
在这个简化的例子中，我们使用了LoRA微调的基本概念：通过引入少量参数来调整一个基准列（或层），从而有效预测其他列（或层）。这与在大型预训练模型中使用LoRA微调的方式类似，只是在实际应用中，微调的参数会更复杂，涉及的数据维度也会更高。这种方法可以显著减少计算资源的需求，同时保持或甚至提高模型在特定任务上的性能。