人工智能uu

这个屌丝很懒，什么也没留下！

热门标签

数据结构——时间复杂度的计算_时间复杂度计算

作者：人工智能uu | 2024-07-17 21:01:54

踩

时间复杂度计算

时间复杂度（Time complexity）是一个函数，它定性描述该算法的运行时间。这是一个代表算法输入值的字符串的长度的函数. 时间复杂度常用大O表述，不包括这个函数的低阶项和首项系数。

时间复杂度大小比较：

常数阶 O(1)<对数阶 O(log2n)<线性阶 O(n)<线性对数阶 O(nlog2n)<平方阶 O(n^2)

<立方阶 O(n^3)<k 次方阶 O(n^k)<指数阶 O(2^n)

图像比较：

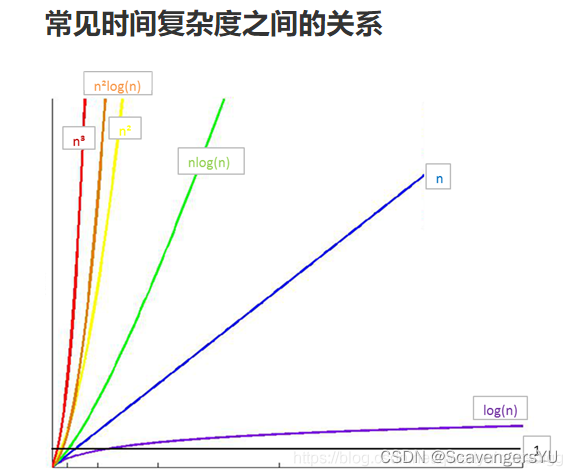
本文旨在总结一些简单易懂的计算时间复杂度的方法。

（1）单层循环

1、列出循环函数中i及每轮循环i的变化值

2、找到i与时间t的关系

3、确定循环停止条件

4、解方程，得到结果

例：


i=n*n;
while(i!=1);
    i=i/2;

时间t	1	2	3	······	t
i	$n^{{2}}$	$\frac{n^{^{2}}}{2}$	$\frac{n^{2}}{4}$	······	$\frac{n^{2}}{2^{t}}$

循环停止条件: i=1;

列出方程: $\frac{n^{2}}{2^{t}}$ =t

解出方程得时间: t=2 $\log_{2}n$

则对应时间复杂度:

T=O( $\log_{2}n$ )

主要是要建立时间与变化量的关系

（2）两层循环

1、列出循环函数中i及每轮循环i的变化值

2、列出内层语句的执行次数

3、两次结果求和,得到结果

例：


int m=0,i,j,m;
for(i=1;i<=n;i++)
    for(j=1;j<=2*i;j++)
        m++

外层函数i的变化值	1	2	······	t
内层函数的执行次数	2	4	······	2*t

外层函数中i的变化值(i从1变成t):t

内层函数执行次数: $\frac{(2*t+2)*t}{2}$ = $t^{2}+t$

求和结果为: $t^{2}+2*t$

则时间复杂化为:

O( $n^{2}$ )

主要是要注意内层函数的执行次数

（3)多层循环

1、方法一:抽象为三维图形体积的计算

2、方法二:列式求和

例：


int i,j,k,s;
for(i=0;i<=n;i++)
    for(j=0;j<=i;j++)
        for(k=0;k<j;k++)
            s++;

方法一: 函数可抽象为三维图形的体积计算

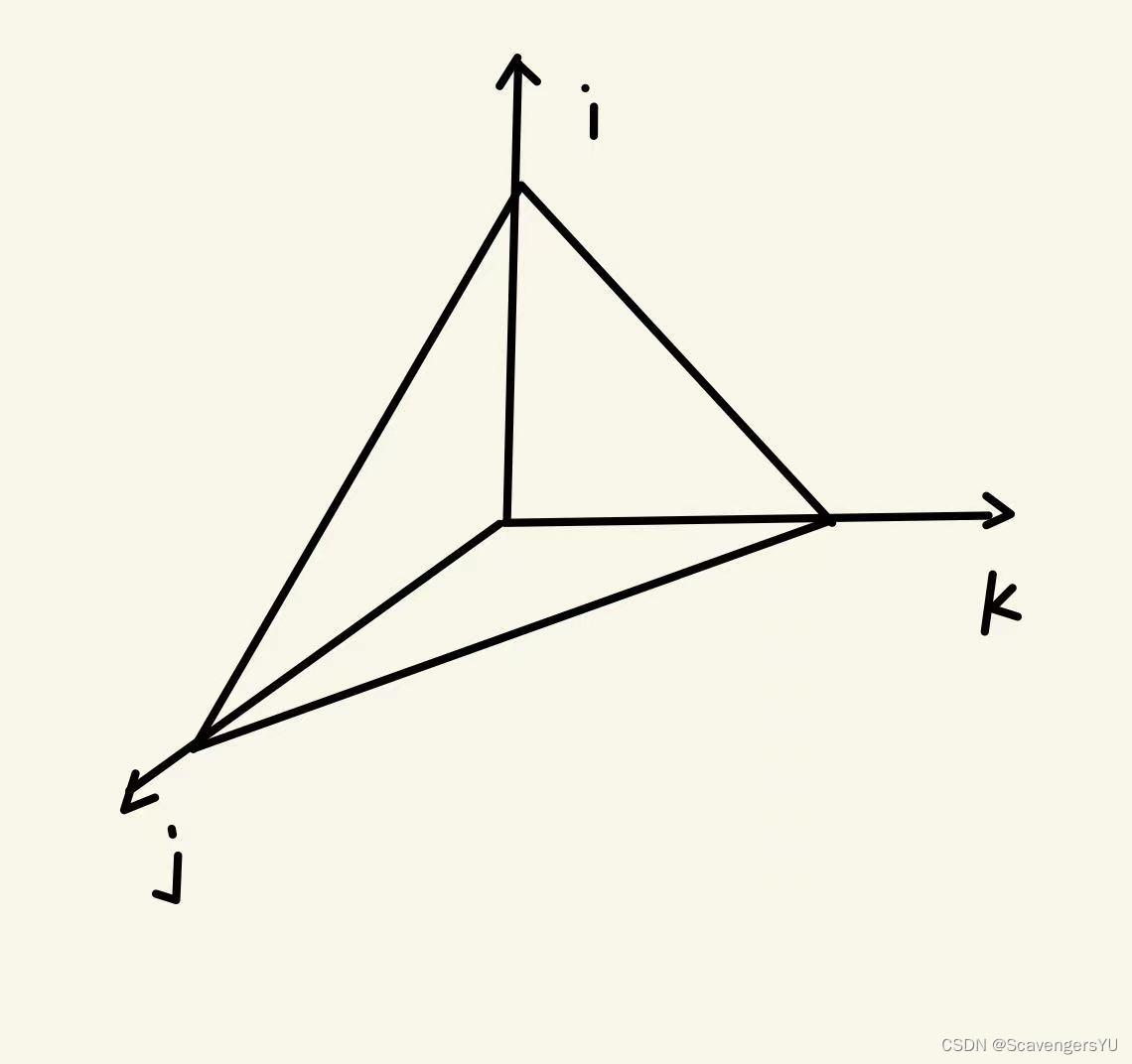
V= $\frac{1}{3}$ SH

得到对应的时间复杂度:

O( $n^{3}$ )

方法二:列项求和

上述式子求和:

$\sum_{i=0}^{n}\sum_{j=0}^{i}\sum_{k=0}^{j-1}=\sum_{i=0}^{n}\sum_{j=0}^{i}(j-1-0+1)=\sum_{i=0}^{n}\sum_{j=0}^{i}j=\sum_{i=0}^{n}\frac{i(i+1)}{2}=\frac{1}{2}\sum_{i=0}^{n}i^{2}+\frac{1}{2}\sum_{i=0}^{n}i=\frac{i^{3}}{2}+\frac{i^{2}}{2}$

得到对应的时间复杂度:

O( $n^{3}$ )

注:上述方法适用于任何形势下的时间复杂度求法,不足之处请大家补充交流,有什么问题可以在评论区留下评论.

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/人工智能uu/article/detail/841990