EM算法及其应用（一）

EM算法是期望最大化 (Expectation Maximization) 算法的简称，用于含有隐变量的情况下，概率模型参数的极大似然估计或极大后验估计。EM算法是一种迭代算法，每次迭代由两步组成：E步，求期望 (expectation)，即利用当前估计的参数值来计算对数似然函数的期望值；M步，求极大 (maximization)，即求参数$\theta$ 来极大化E步中的期望值，而求出的参数$\theta$将继续用于下一个E步中期望值的估计。EM算法在机器学习中应用广泛，本篇和下篇文章分别探讨EM算法的原理和其两大应用 —— K-means和高斯混合模型。

$\large{\S} \normalsize\mathrm{1}$ 先验知识

---

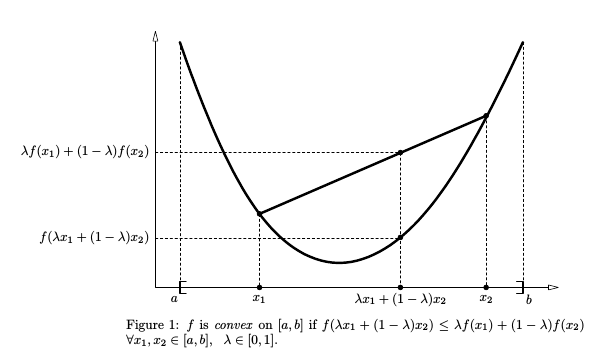
凸函数、凹函数和 Jensen不等式

设$f(x)$为定义在区间$I = [a,b]$上的实值函数，对于任意$\forall \, x_1, x_2 \in I, \lambda \in [0,1]$，有：

$$f(\lambda \,x_1 + (1-\lambda)\,x_2) \leq \lambda f(x_1) + (1-\lambda)f(x_2)$$
则$f(x)$为凸函数 (convex function)，如下图所示。相应的，若上式中 $\leqslant$ 变为 $\geqslant$ ，则$f(x)$为凹函数 (concave function)。 凸函数的判定条件是二阶导 $f^{''}(x) \geqslant 0$，而凹函数为 $f^{''}(x) \leqslant 0$ 。后文要用到的对数函数$ln(x)$的二阶导为$-\frac{1}{x^2} < 0$，所以是凹函数。

Jensen不等式就是上式的推广，设$f(x)$为凸函数，$\lambda_i \geqslant 0, \;\; \sum_i \lambda_i = 1$，则：

$$f\left(\sum\limits_{i=1}^n \lambda_i x_i\right) \leq \sum\limits_{i=1}^n \lambda_i f(x_i)$$
如果是凹函数，则将不等号反向，若用对数函数来表示，就是：
$$ln\left(\sum\limits_{i=1}^n \lambda_i x_i\right) \geq \sum\limits_{i=1}^n \lambda_i ln(x_i)$$
若将$\lambda_i$视为一个概率分布，则可表示为期望值的形式，在后文中同样会引入概率分布：
$$f(\mathbb{E}[\mathrm{x}]) \leq \mathbb{E}[f(\mathrm{x})]$$

KL散度

KL散度(Kullback-Leibler divergence) 又称相对熵 (relative entropy)，主要用于衡量两个概率分布p和q的差异，也可理解为两个分布对数差的期望。

$$\mathbb{KL}(p||q) = \sum_i p(x_i)log \frac{p(x_i)}{q(x_i)}= \mathbb{E}_{\mathrm{x}\sim p}\left[log \frac{p(x)}{q(x)}\right] = \mathbb{E}_{\mathrm{x}\sim p}\left[log\,p(x) - log\,q(x) \right ]$$
KL散度总满足$\mathbb{KL}(p||q) \geqslant 0$，而当且仅当$q=p$时，$\mathbb{KL}(p||q) = 0$ 。 一般来说分布$p(x)$比较复杂，因而希望用比较简单的$q(x)$去近似$p(x)$，而近似的标准就是KL散度越小越好。

KL散度不具备对称性，即$\mathbb{KL}(p||q) \neq \mathbb{KL}(q||p)$，因此不能作为一个距离指标。

极大似然估计和极大后验估计

极大似然估计 (Maximum likelihood estimation) 是参数估计的常用方法，基本思想是在给定样本集的情况下，求使得该样本集出现的“可能性”最大的参数$\theta$。将参数$\theta$视为未知量，则参数$\theta$对于样本集X的对数似然函数为：

$$L(\theta) = ln \,P(X|\theta)$$
这个函数反映了在观测结果X已知的条件下，$\theta$的各种值的“似然程度”。这里是把观测值X看成结果，把参数$\theta$看成是导致这个结果的原因。参数$\theta$虽然未知但是有着固定值 (当然这是频率学派的观点)，并非事件或随机变量，无概率可言，因而改用 “似然(likelihood)" 这个词。

于是通过求导求解使得对数似然函数最大的参数$\theta$，$\theta = \mathop{\arg\max}\limits_{\theta}L(\theta)$，即为极大似然法。

极大后验估计 (Maximum a posteriori estimation) 是贝叶斯学派的参数估计方法，相比于频率学派，贝叶斯学派将参数$\theta$视为随机变量，并将其先验分布$P(\theta)$包含在估计过程中。运用贝叶斯定理，参数$\theta$的后验分布为：

$$P(\theta|X) = \frac{P(X,\theta)}{P(X)} = \frac{P(\theta)P(X|\theta)}{P(X)} \propto P(\theta)P(X|\theta)$$
上式中$P(X)$不依赖于$\theta$因而为常数项可以舍去，则最终结果为 $\theta = \mathop{\arg\max}\limits_{\theta}P(\theta)P(X|\theta)$

$\large{\S} \normalsize\mathrm{2}$ EM算法初探

---

概率模型有时既含有观测变量 (observable variable)，又含有隐变量 (hidden variable)，隐变量顾名思义就是无法被观测到的变量。如果都是观测变量，则给定数据，可以直接使用极大似然估计。但如果模型含有隐变量时，直接求导得到参数比较困难。而EM算法就是解决此类问题的常用方法。

对于一个含有隐变量$\mathbf{Z}$的概率模型，一般将$\{\mathbf{X}, \mathbf{Z}\}$称为完全数据，而观测数据$\mathbf{X}$为不完全数据。

我们的目标是极大化观测数据$\mathbf{X}$关于参数$\boldsymbol{\theta}$的对数似然函数。由于存在隐变量，因而也可表示为极大化$\mathbf{X}$的边缘分布 (marginal distribution)，即：

$$L(\boldsymbol{\theta}) = ln\,P(\mathbf{X}|\boldsymbol{\theta}) = ln\,\sum\limits_{\mathbf{Z}}P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}) \tag{1.1}$$
上式中存在“对数的和” —— $ln\sum(\cdot)$，如果直接求导将会非常困难。因而EM算法采用曲线救国的策略，构建$(1.1)$式的一个下界，然后通过极大化这个下界来间接达到极大化$(1.1)$的效果。

要想构建下界，就需要运用上文中的Jensen不等式。记$\boldsymbol{\theta}^{(t)}$为第t步迭代参数的估计值，考虑引入一个分布$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})$，由于：

1. $P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)}) \geqslant 0$
2. $\sum_{\mathbf{Z}}P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)}) = 1$
3. $ln(\cdot)$为凹函数

因而可以利用Jensen不等式求出$L(\boldsymbol{\theta})$的下界：

$$\begin{align} L(\boldsymbol{\theta}) = ln\,\sum\limits_{\mathbf{Z}}P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}) &= ln\,\sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}})\frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}) }{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})} \tag{1.2}\\ & \geqslant \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln\frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}) }{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})} \tag{1.3} \\ & = \underbrace{\sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}) }}_{\mathcal{Q}(\boldsymbol{\theta},\boldsymbol{\theta}^{(t)})} \;\;\underbrace{- \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})}}_{entropy} \tag{1.4} \end{align}$$
$(1.3)$式构成了$L(\boldsymbol{\theta})$的下界，而$(1.4)$式的右边为$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})的熵 \geqslant 0$ ，其独立于我们想要优化的参数$\boldsymbol{\theta}$，因而是一个常数。所以极大化$L(\boldsymbol{\theta})$的下界$(1.3)$式就等价于极大化$\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)})$，$\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)})$ (Q函数) 亦可表示为 $\,\mathbb{E}_{\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)}}\,lnP(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})$，其完整定义如下：

基于观测数据 $\mathbf{X}$ 和 当前参数$\theta^{(t)}$计算未观测数据 $\mathbf{Z}$ 的条件概率分布$P(\mathbf{Z}|\mathbf{X}, \theta^{(t)})$，则Q函数为完全数据的对数似然函数关于$\mathbf{Z}$的期望。

此即E步中期望值的来历。

接下来来看M步。在$(1.3)$式中若令$\boldsymbol{\theta} = \boldsymbol{\theta}^{(t)}$，则下界$(1.3)$式变为：

$$\begin{align*} & \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln\frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta}^{(t)}) }{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})} \\ =\;\; & \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln\frac{P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}})P(\mathbf{X}|\boldsymbol{\theta}^{(t)})}{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})} \\ = \;\; & \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,lnP(\mathbf{X}|\boldsymbol{\theta}^{(t)}) \\ = \;\; & lnP(\mathbf{X}|\boldsymbol{\theta}^{(t)}) \;\;=\;\; L(\boldsymbol{\theta}^{(t)}) \end{align*}$$
可以看到在第t步，$L(\boldsymbol{\theta}^{(t)})$的下界与$L(\boldsymbol{\theta}^{(t)})$相等，又由于极大化下界与极大化Q函数等价，因而在M步选择一个新的$\boldsymbol{\theta}$来极大化$\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)})$，就能使$L(\boldsymbol{\theta}) \geqslant \mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)}) \geqslant \mathcal{Q}(\boldsymbol{\theta}^{(t)}, \boldsymbol{\theta}^{(t)}) = L(\boldsymbol{\theta}^{(t)})$ (这里为了便于理解就将$\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)})$与$(1.3)$式等同了)，也就是说$L(\boldsymbol{\theta})$是单调递增的，通过EM算法的不断迭代能保证收敛到局部最大值。

EM算法流程：

输入： 观测数据$\mathbf{X}$，隐变量$\mathbf{Z}$，联合概率分布$P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})$

输出：模型参数$\boldsymbol{\theta}$

1. 初始化参数$\boldsymbol{\theta}^{(0)}$
2. E步： 利用当前参数$\boldsymbol{\theta}^{(t)}$计算Q函数， $\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)}) = \sum\limits_{\mathbf{Z}}P(\mathbf{Z|\mathbf{X},\boldsymbol{\theta}^{(t)}}) \,ln{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})}$
3. M步： 极大化Q函数，求出相应的 $\boldsymbol{\theta} = \mathop{argmax}\limits_{\boldsymbol{\theta}}\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)})$
4. 重复 2. 和3. 步直至收敛。

EM算法也可用于极大后验估计，极大后验估计仅仅是在极大似然估计的基础上加上参数$\boldsymbol{\theta}$的先验分布，即 $p(\boldsymbol{\theta})p(\mathbf{X}|\boldsymbol{\theta})$，则取对数后变为$ln\,p(\mathbf{X}|\boldsymbol{\theta}) + ln\,p(\boldsymbol{\theta})$，由于后面的$ln\,p(\boldsymbol{\theta})$不包含隐变量$\mathbf{Z}$，所以E步中求Q函数的步骤不变。而在M步中需要求新的参数$\mathbf{\theta}$，因此需要包含这一项，所以M步变为

$$\boldsymbol{\theta} = \mathop{argmax}\limits_{\boldsymbol{\theta}} \left[\mathcal{Q}(\boldsymbol{\theta}, \boldsymbol{\theta}^{(t)}) + ln(p(\boldsymbol{\theta})\right]$$

$\large{\S} \normalsize\mathrm{3}$ EM算法深入

---

上一节中遗留了一个问题：为什么式$(1.2)$中引入的分布是$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{(t)})$而不是其他分布？ 下面以另一个角度来阐述。

假设一个关于隐变量$\mathbf{Z}$的任意分布$q(\mathbf{Z})$，则运用期望值的定义，$(1.1)$式变为：

$$\begin{align*} L(\boldsymbol{\theta}) = lnP(\mathbf{X}|\boldsymbol{\theta}) &= \sum\limits_{\mathbf{Z}}q(\mathbf{Z})\,lnP(\mathbf{X}|\boldsymbol{\theta}) \quad\qquad \text{上下同乘以 $q(\mathbf{Z}) \,P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})$}\\ & = \sum\limits_{\mathbf{Z}}q(\mathbf{Z}) ln\frac{P(\mathbf{X}|\boldsymbol{\theta})q(\mathbf{Z}) P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})}{q(\mathbf{Z}) P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})} \\ & = \sum\limits_{\mathbf{Z}}q(\mathbf{Z}) \frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})}{q(\mathbf{Z})} + \sum\limits_{\mathbf{Z}}q(\mathbf{Z}) ln \frac{P(\mathbf{X}|\boldsymbol{\theta})q(\mathbf{Z}) }{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})} \\ & = \sum\limits_{\mathbf{Z}}q(\mathbf{Z}) \frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})}{q(\mathbf{Z})} + \sum\limits_{\mathbf{Z}}q(\mathbf{Z}) ln \frac{q(\mathbf{Z}) }{P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta})} \\ & = \underbrace{\sum\limits_{\mathbf{Z}}q(\mathbf{Z}) \frac{P(\mathbf{X},\mathbf{Z}|\boldsymbol{\theta})}{q(\mathbf{Z})}}_{L(q,\boldsymbol{\theta})} + \mathbb{KL}(q(\mathbf{Z})||P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}))) \tag{2.1} \end{align*}$$
$(2.1)$式的右端为$q(\mathbf{Z})$和后验分布$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta})$的KL散度，由此 $lnP(\mathbf{X}|\boldsymbol{\theta})$被分解为$L(q,\boldsymbol{\theta})$和$\mathbb{KL}(q||p)$ 。由于KL散度总大于等于0，所以$L(q,\boldsymbol{\theta})$是$lnP(\mathbf{X}|\boldsymbol{\theta})$的下界，如图：

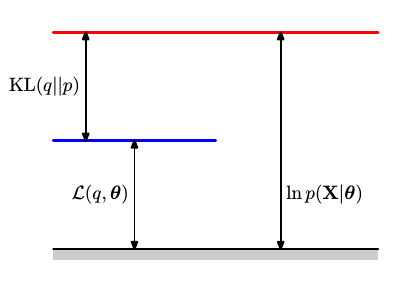
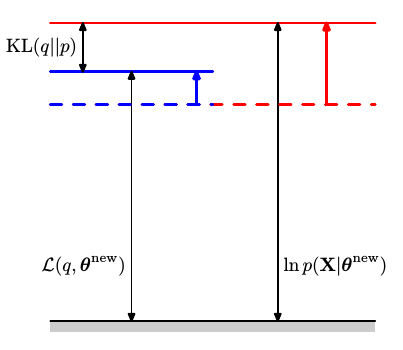
由此可将EM算法视为一个坐标提升(coordinate ascent)的方法，分别在E步和M步不断提升下界$L(q,\boldsymbol{\theta})$，进而提升$lnP(\mathbf{X}|\boldsymbol{\theta})$ 。


在E步中，固定参数$\boldsymbol{\theta}^{old}$，当且仅当$\mathbb{KL}(q||p) = 0$，即$L(q,\boldsymbol{\theta}) = lnP(\mathbf{X}|\boldsymbol{\theta})$时，$L(q,\boldsymbol{\theta})$达到最大，而$\mathbb{KL}(q||p) = 0$的条件是$q(\mathbf{Z}) = P(\mathbf{Z}|\mathbf{X}, \boldsymbol{\theta})$，因此这就是式$(1.2)$中选择分布$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{old})$的原因，如此一来$L(q,\boldsymbol{\theta})$ 也就与$(1.3)$式一致了。

在M步中，固定分布$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{old})$，选择新的$\boldsymbol{\theta}^{new}$来极大化$L(q,\boldsymbol{\theta})$ 。同时由于$P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{old}) \neq P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{new})$，所以$\mathbb{KL}(P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{old}) || P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{new})) > 0$，导致$lnP(\mathbf{X}|\boldsymbol{\theta})$提升的幅度会大于$L(q,\boldsymbol{\theta})$提升的幅度，如图：

因此在EM算法的迭代过程中，通过交替固定$\boldsymbol{\theta}$ 和 $P(\mathbf{Z}|\mathbf{X},\boldsymbol{\theta}^{old})$来提升下界$L(q,\boldsymbol{\theta})$ ，进而提升对数似然函数$L(\boldsymbol{\theta})$ ，从而在隐变量存在的情况下实现了极大似然估计。在下一篇中将探讨EM算法的具体应用。

Reference:

1. Christopher M. Bishop. Pattern Recognition and Machine Learning
2. 李航. 《统计学习方法》
3. CS838. The EM Algorithm

/