[数据结构]图解链表，附带leetcode刷题，妈妈再也不担心我不懂链表了_图结构 提取 链表

【前言】详细的介绍了链表的相关知识。所用语言---c

链表的表示与实现

顺序表与链表的区别与联系

leetcode刷题

请在看代码时，自己也动手画起来，才能理解的更深刻。学习数据结构是一定要画图的！！！

目录

1单链表

2.双链表

3.链表相关oj题（来源leetcode）

3.1反转链表（笔试常考）

3.2查找链表的中间节点

3.3合并两个有序链表

3.4环形链表（较难）

---

 

上一篇我们讲解了顺序表，但不管是动态还是静态，顺序表是存在很多缺陷的。

如果空间不够需要扩容，扩容多了很容易造成空间的浪费，扩少了扩容次数又要多。

另外就是插入删除的效率太低了。

那么会这样思考，有没有一种方法可以达到“按需索取”的效果，我要存220个元素，那就有220个空间去存，而不会过大的扩容造成浪费呢？而且若不要求物理地址连续的话，其删除插入操作将不需要大量的挪动数据。这样是不是相较于顺序表会更方便呢？

答案是使用指针相连贯前后的链表。

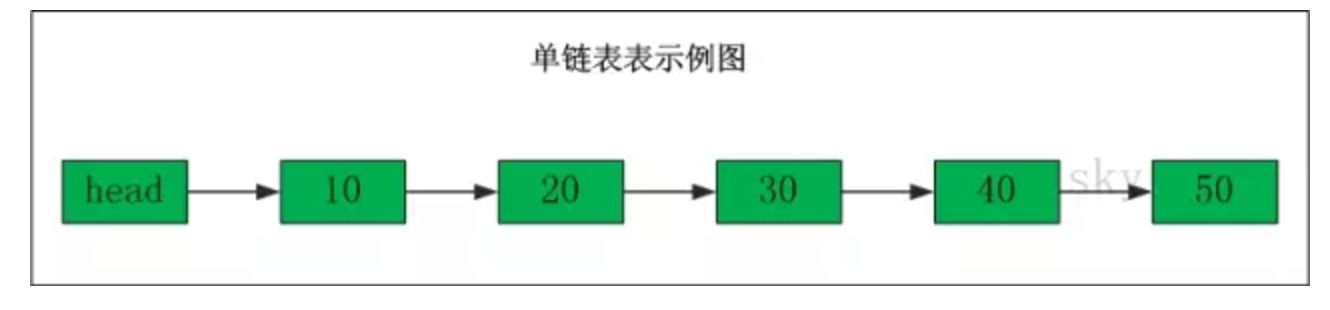
链表是一种物理存储结构非连续的存储结构，数据元素的逻辑顺序由指针链接来实现。

接下来就来看看单链表的表示与实现过程吧。

1单链表

（图源百度百科）

其中的next就是指向下一个节点的指针。

 

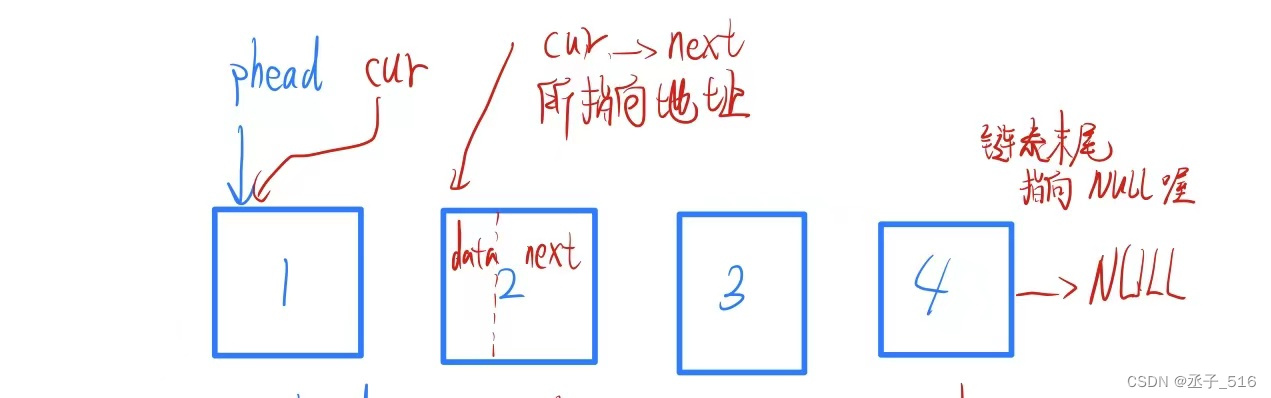
 上图所展示的是一种逻辑结构，但在物理上，链表的存储是不连续的。节点node1的指针种存储的就是node2的第一个字节的地址。当结束时，如上图所示，节点n的指针指向的是NULL

第一步仍然还是定义一个结构体，包含一个节点的数据data与指向下一个节点的指针next

typedef int datatype;
typedef struct slistnode
{
	datatype data;
	struct slistnode* next;//指向这种类型的指针，但注意，结构体不能嵌套结构体哦
 
}snode;

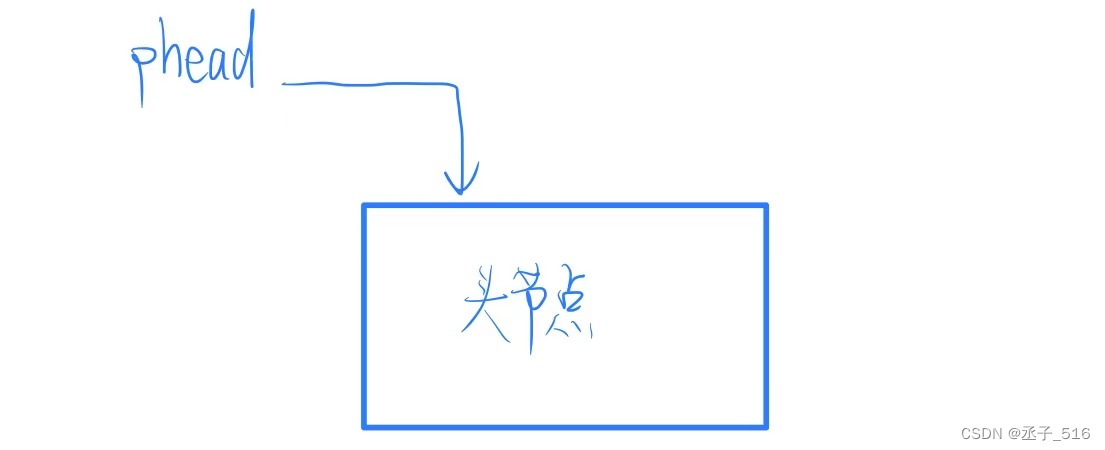
除此之外还需要一个phead，用以指向头节点，在初始化常置为NULL

再来介绍链表的打印，其中的cur=cur->next是需要重点理解的一个地方。

 

//打印链表
void printslist(snode* phead)
{   //创建一个指针指向phead的下一个节点
	snode* cur = phead;
	while (cur != NULL)  //当cur移动到NULL时，即遍历完整个链表。
	{
		printf("%d", cur->data);
		cur = cur->next; //cur指向此结构体中的next，也就是下一个节点的data。
	}
 
}

接下来先介绍尾插法。

 

//尾插
void slistpushback(snode** pphead,datatype x)
{
	snode* newnode = (snode*)malloc(sizeof(snode));//创建一个新节点
	newnode->data = x;
	newnode->next = NULL;//注意不要忘了最后一个节点的next指向NULL哦
	if (*pphead == NULL)
	{
		*pphead = newnode;
	}
	else
	{
		//利用tail来找链表尾巴
		snode* tail = *pphead;
		while (tail->next != NULL)
		{
			tail = tail->next;
		}
		//链接尾节点
		tail->next = newnode;
	}
}

其中有需要注意的几个地方。

1. 在利用tail去寻找链表的尾巴时，不能使用while(tail != next)，而是tail.next不为空，最后tail才能指向尾节点，否则tail将会指向尾节点之后。

这一点如果无法理解建议自己画一个链表来逐步的画出步骤，这样可以加深你对链表尾插的理解。

2.为什么使用二级指针来传入函数参数？我们想要改变的是phead。所以根据形参是实参的一份拷贝的说法，如果传入phead，那么函数里的phead作为形参，其改变是无法影响实参的。所以我们就用了指针的指针来唯一的标识phead，也就是将指针phead的地址当作了门牌号，我们通过门牌号来访问phead。

3.为何要判断我们插入的是不是首个节点？最开始链表为空，则只有一个phead，phead指向为空，tail也是空的，那么tail->next又从何谈起呢？所以需要在插入首节点时直接将phead=newnode

这也就是三个比较重要的需要理解的点。如果到这里能全部理解的话，后面的知识点就会易懂很多了。

那么就可以对其进行测试了。

void testlist()
{
	snode* phead = NULL;
	slistpushback(&phead, 3);
	slistpushback(&phead, 3);
	slistpushback(&phead, 3);
	slistpushback(&phead, 3);
	printslist(phead);
}

经过测试确实打印出了3 3 3 3，证明函数书写无误。

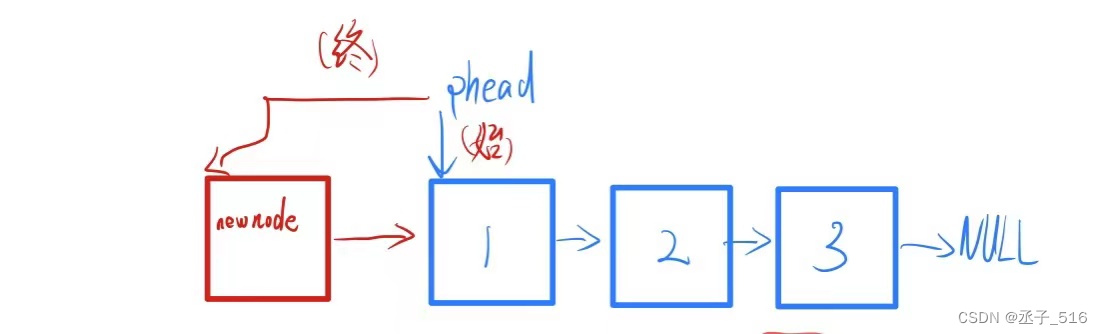
头插法就简单很多了。

 

//头插
void slistpushfront(snode** pphead, datatype x)
{
	snode* newnode = (snode*)malloc(sizeof(snode));//创建一个新节点
	newnode->data = x;
	newnode->next = NULL;//注意不要忘了最后一个节点的next指向NULL哦
	newnode->next = *pphead;
	*pphead = newnode;
}

不管链表里有无节点，进行头插都是一样的代码，这点不同于尾插，尾插需要考虑tail无法指向NULL的情况。

头删法：

 

 

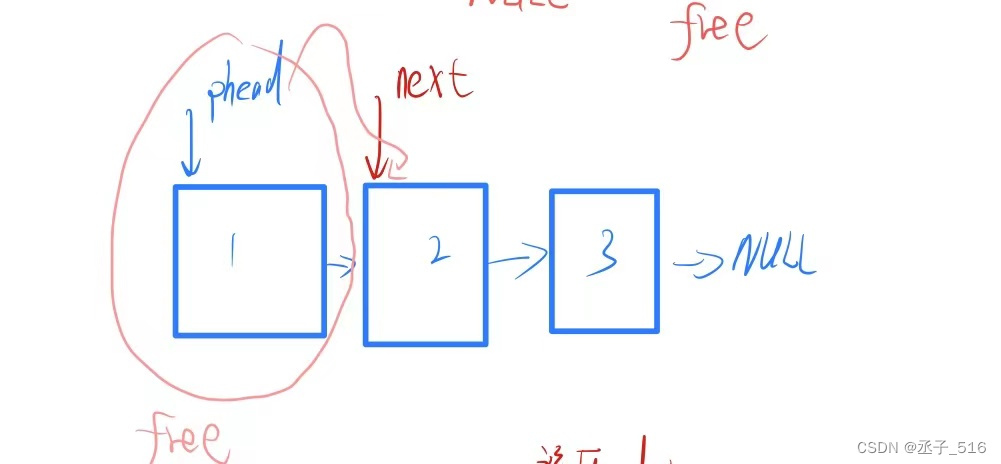
//头删
void slistpopfront(snode** pphead)
{
	//用一个指针保存头节点的next（也就是第二个节点），再释放第一个节点
	snode* next = (*pphead)->next;
	free(*pphead);
	//将第二个节点地址存入phead
	*pphead = next;
}

尾删法：

重点是找到tail的前一个，不然将tail那个节点释放了，tail前一个的地址去哪里找呢？我们需要将tail的前一个置为NULL才行啊，否则变成了野指针的话会造成很多难以预料的结果。

 

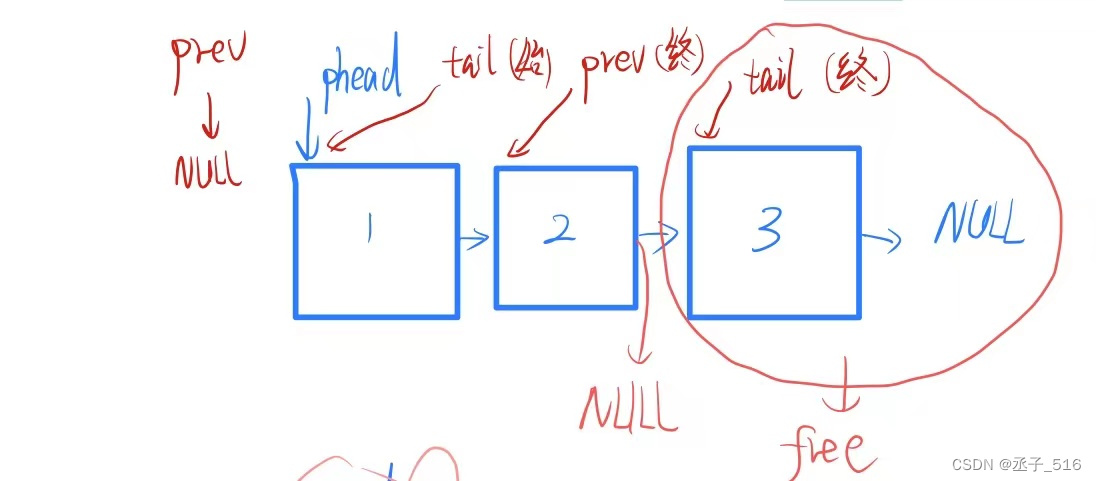
//尾删
void slistpopback(snode** pphead)
{
	//主要是要找到尾的前一个，将其置向null，不然就成了野指针了。
 
	if (*pphead==NULL)  
	{
		return;
	}
	else if ((*pphead)->next == NULL)
	{
		free(*pphead);
		*pphead = NULL;
	}
	snode* prev = NULL;
	snode* tail = *pphead;
	while (tail->next != NULL)
	{
		prev = tail;
		tail = tail->next;
	}
	free(tail);
	prev->next = NULL;
}

还是用常用的方法，使用两个指针，当tail向后移动时，prev移动到tail的前一个节点的位置就好了。

参考上文，如果为空链表，那么tail.next仍然会出现问题。所以我们添加了判断，如果为空则直接返回。

若是有一个节点呢？那么prev.next会出现同样的问题，则还需多判断只有一个节点的情况。

都如上图代码所示了。不理解的请画图加深印象。

接下来介绍查找元素，并在其前面插入元素的方法。

查找：

 

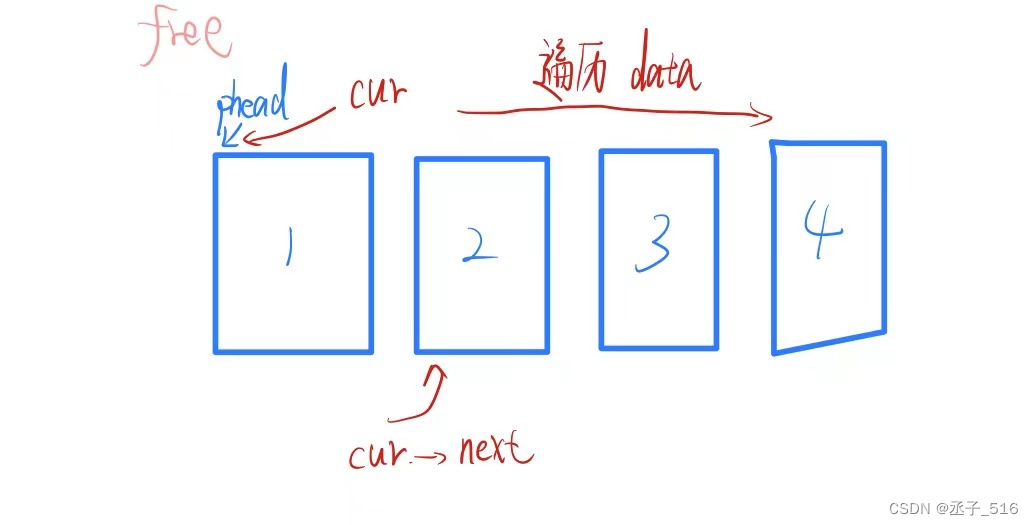
//查找
snode* slistfind(snode* phead, datatype x)
{
	snode* cur = phead;
	while (cur)
	{
		if (cur->data == x)
		{
			return cur;
		}
		cur = cur->next;
	}
	reutrn NULL;
}

如何插入呢？还是有老问题，我们知道cur，却不知道cur指向的上一个节点在哪里。所以仍然需要两个指针。或者用下面这种方法，只用一个prev，然后判断prev.next的情况。

 

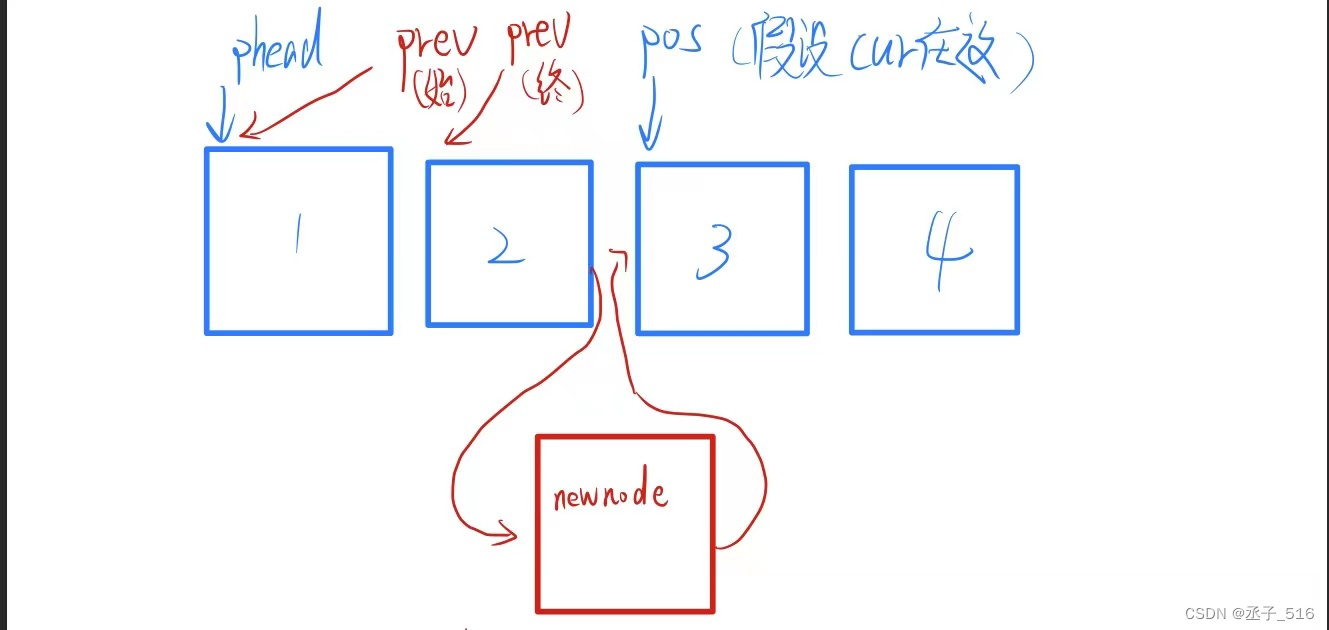
//插入
void slistinsert(snode** pphead, snode* pos, datatype x)
{
	if (pos == *pphead)  // 当pos就在第一个位置时，直接相当于头插，如果不这样，prev无法判断pos位，他的起始判断位置就在prev->next
	{
		slistpushfront(pphead, x);
	}
	else
	{
 
		snode* newnode = (snode*)malloc(sizeof(snode));//创建一个新节点
		newnode->data = x;
		newnode->next = NULL;
		snode* prev = *pphead;
		while ((prev->next) != pos)
		{
			prev = prev->next;
		}
		prev->next = newnode;
		newnode->next = pos;
	}
}

 接下来讲解如何删除

 

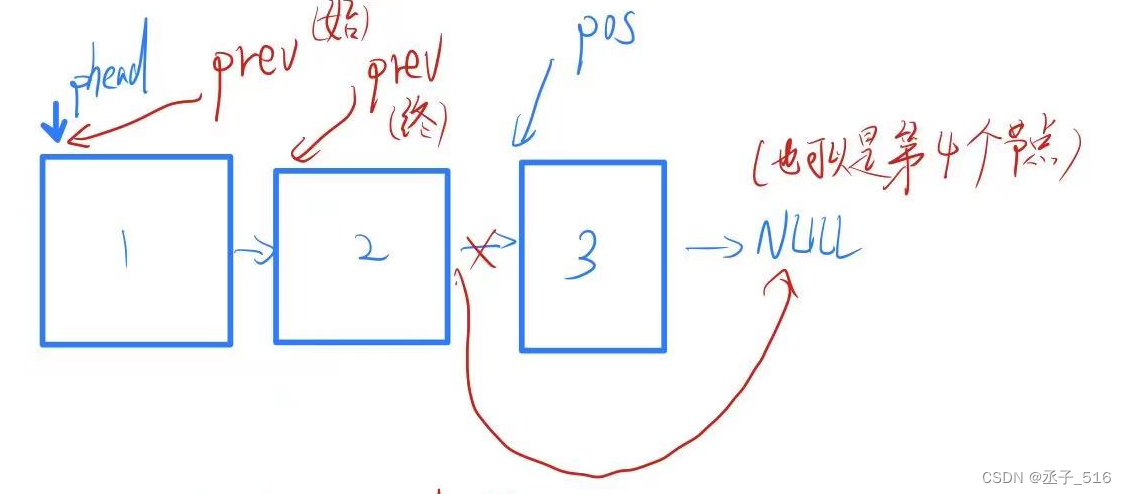
//删除
void slisterase(snode** pphead, snode* pos)
{
	snode* prev = *pphead;
	while (prev->next != pos)
	{
		prev = prev->next;
	}
	prev->next = pos->next;
	free(pos);
}

但头删出现了问题。

改进，当头删时需要单独考虑

//删除
void slisterase(snode** pphead, snode* pos)
{
	if (pos == *pphead)
	{
		slistpopfront(pphead);
	}
	else
	{
		snode* prev = *pphead;
		while (prev->next != pos)
		{
			prev = prev->next;
		}
		prev->next = pos->next;
		free(pos);
	}
}

以上就是单链表的全部操作了。

但单链表是存在缺陷的。例如查找速度慢，找不到前驱，不能从后往前等等的问题。

在实现尾插，尾删，插入时大多具有O（N）的时间复杂度，而造成这样的原因也是因为找到前一个很困难。以此我们提出了双向链表。

2.双链表

 双向链表不仅有后继，还具备前驱。相比单链表会更适用。

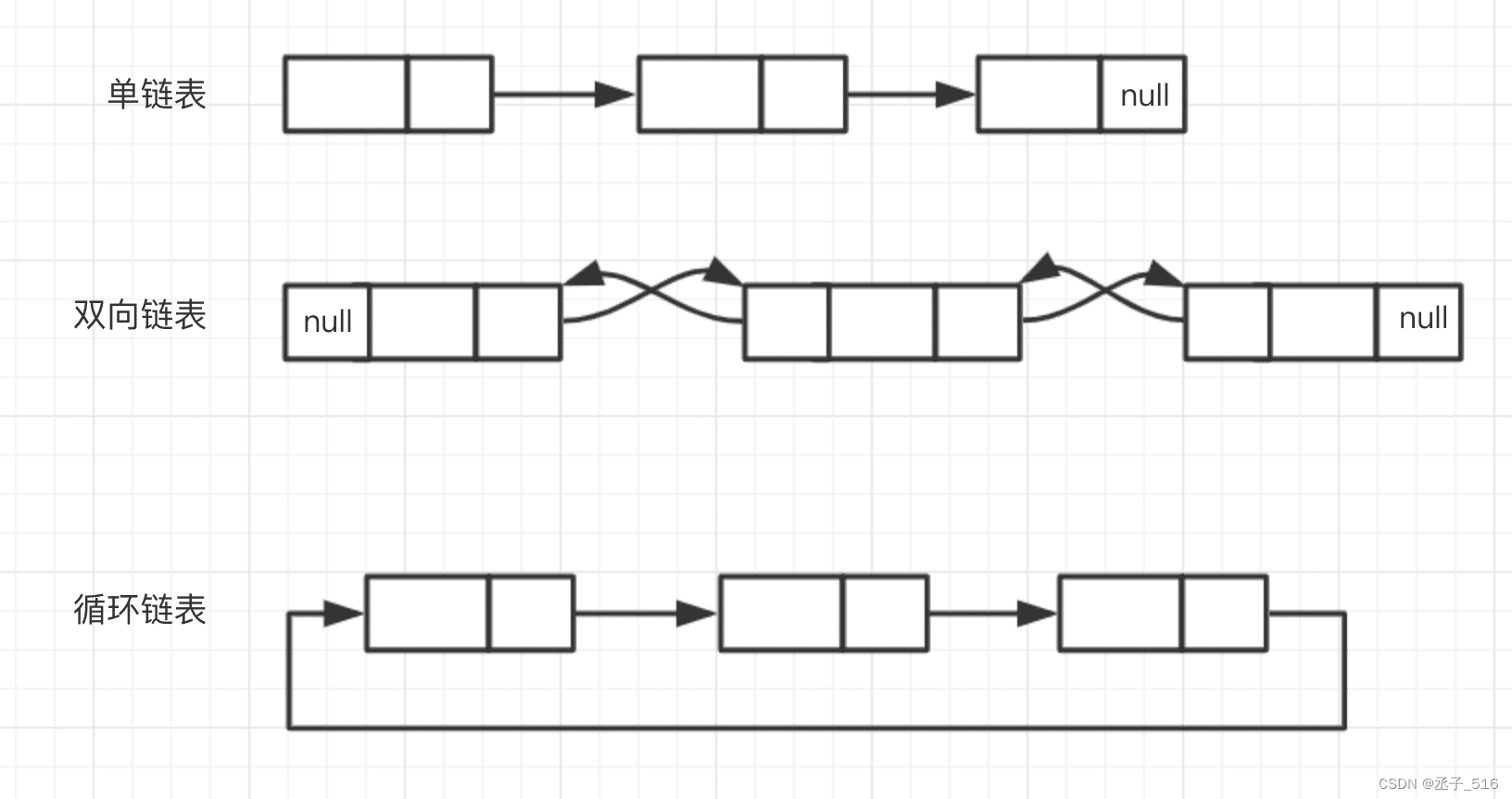
（图源百度百科） 

先来介绍一下带哨兵位的头节点，我们将phead指向的第一个节点（存储第一个节点的地址），但是第一个节点不存有效数据，那么在进行一些接口函数的实现时，就不需要再传二级指针了。因为不需要改变这个哨兵位。

但是请注意，哨兵位不要写入链表长度这样的操作，因为链表不应该只限制一种数据的存入，可以同时存入多种类型数据。

所以我们使用哨兵位主要就是为了不使用二级指针。

再来介绍下循环，尾指向头就是循环，指向空就是不循环，所以单向，双向，带头，不带头，循环，不循环，可以组成八种不同类型的链表。

最简单的无头单向非循环链表，结构是最简单的，但是不会用来单独存数据，而是作为了一些数据结构的子结构来使用。在一些笔试面试中适用场景出现非常多。

而带头双向循环链表，作为最复杂的一种结构，就是我们今天要讲解的例子，虽然实现复杂，但是会带来很多的优势，实现反而更加的简单。

请一定要熟练掌握以上两种链表。

话不多说，上代码开始讲解。

第一步老规矩，还是先写节点的结构体。

typedef int datatype;
struct listnode
{
	struct listnode* next;
    struct listnide* prev;
	datatype data;
};

紧接着的就是初始化操作。

在初始化的时候要注意是带有哨兵位的，而且如果要循环，请一定将next和prev指向自己。之后就明白其奇妙之处了，初始化是需要改变phead的，所以可以如上文所示传入二级指针对phead进行一个更改，在此不多赘述，而是提供一个不需要传入二级指针的办法。

//初始化
listnode* listinit()
{
	//申请新节点。
	listnode* phead = (listnode*)malloc(sizeof(listnode));
	phead->data = 0;
	phead->next =phead;  //指向自己
	phead->prev = phead;
	return phead;
 
}
void test()
{
	
	listnode* phead=listinit();
 
 
	
}

如上所示，和上文不一样的是，我们选择了返回一个phead，所以将函数前类型改成listnode* 

 这样就不用使用二级指针了。

接下来介绍尾插法。此时循环的好处就体现出来了。

此时找尾就直接可以找到了。phead的prev即是尾了。

 

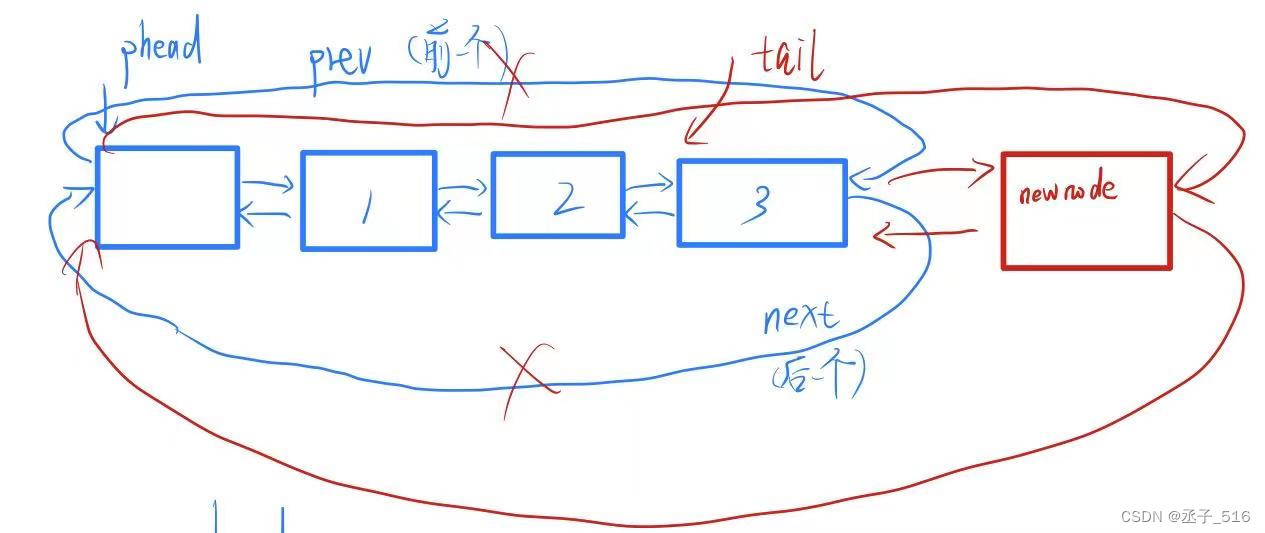
/尾插
void listpushback(listnode* phead,datatype x)
{
	listnode* tail = phead->prev;
	listnode* newnode = (listnode*)malloc(sizeof(listnode));
	newnode->data = x;
	//核心代码，不理解请一定要画图哦
	tail->next = newnode;
	newnode->prev = tail;
	newnode->next = phead;
	phead->prev = newnode;
	
	
}

同时可以发现的是，不管链表是不是为空，都是适用的，所以不需要单独讨论空链表的情况。

接下来是头插法。

就是在phead这个哨兵位和插入了有效数据的第一个节点（我们记为first）之间。

 

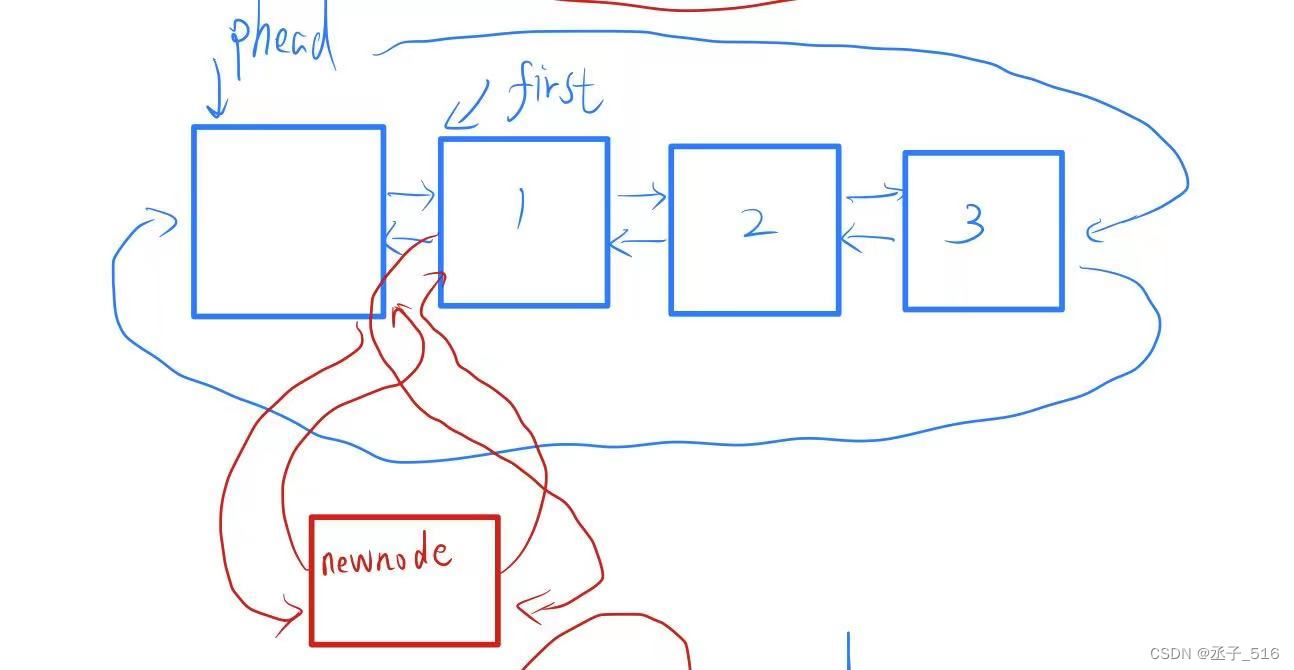
void listfrontpush(listnode* phead, datatype x)
{
	listnode* first = phead->next;
	listnode* newnode = (listnode*)malloc(sizeof(listnode));
	newnode->data = x;
	phead->next = newnode;
	newnode->prev = phead;
	newnode->next = first;
	first->prev = newnode;
	
}

 头删法：

仍然将first指向第一个节点（带有有效数据的），second指向第二个

 

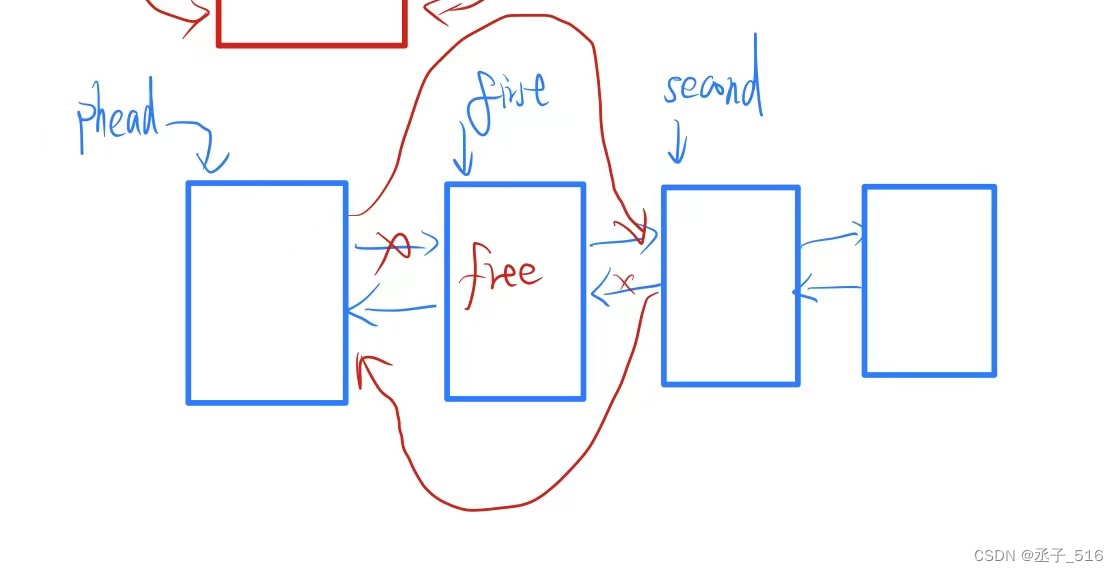
void listfrontpop(listnode* phead)
{
	assert(phead->next != phead);
	listnode* first = phead->next;
	listnode* second = first->next;
	phead->next = second;
	second->prev = phead;
	free(first);
	
}

注意只剩phead就不要再删了。

尾删法也是同样的思路，只需要有倒数两个节点就行，不断地改变next和prev的指向就ok了。

//尾删
void listbackpop(listnode* phead)
{
	assert(phead->next != phead);
	listnode* tail = phead->prev;
	listnode* prev = tail->prev;
	prev->next = phead;
	phead->prev = prev;
	free(tail);
	//listerase(phead->prev);
}

接下来就是在pos位置前进行插入的操作。

仍然需要通过指针找到pos的位置才行。

非常简单，定义一个cur指针从头遍历到尾即可，没有就返回NULL即可。

//查找pos
listnode* listfind(listnode* phead, datatype x)
{
	assert(phead);
	listnode* cur = phead->next;
	while (cur != phead)
	{
		if (cur->data == x)
		{
			return cur;
		}cur = cur->next;
	}
	return NULL;
}

这样就找到了我们需要寻找的数据的位置。同时通过设置assert和一些判断语句增强了代码的严谨性。

而且查找函数可以充当改的函数。将cur的指向的位置的data进行更改即可。

查找附带着修改data的作用。

接下来介绍插入

 

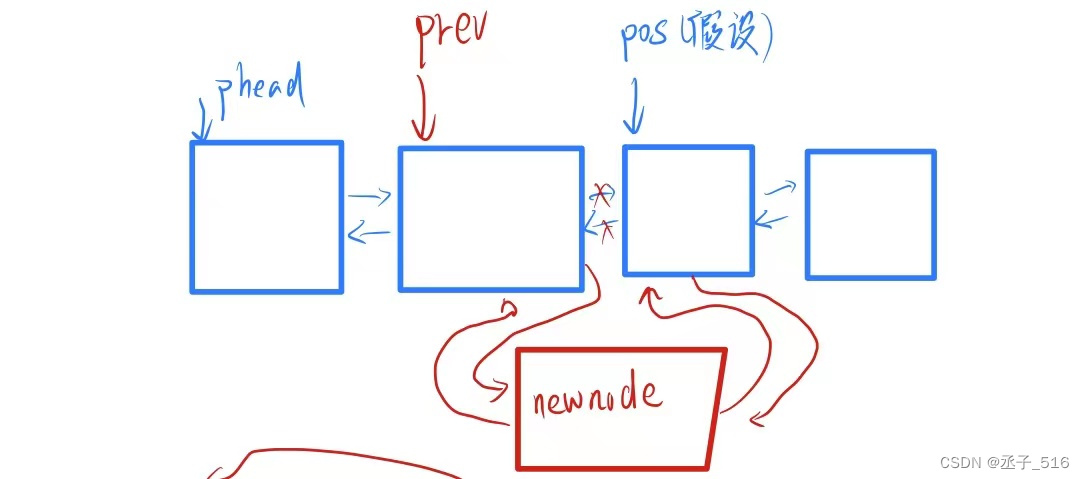
//插入
void listinsert(listnode* pos, datatype x)
{
	assert(pos);
	listnode* prev = pos->prev;
	//申请节点
	listnode* newnode = (listnode*)malloc(sizeof(listnode));
	newnode->data = x;
	newnode->next = pos;
	prev->next = newnode;
	newnode->prev = prev;
	pos->prev = newnode;
 
}

可以发现的是，如果不想对指针指向的修改有顺序的限制，那么只需多定义一个指针prev，就可以随意的对指针的指向进行修改了。非常的方便，如果只有一个pos的话就要考虑到改变指向的顺序了。

怎么进行删除呢？

删除也是同样的道理，定义出prev和next，直接更改就完了，而且哪怕pos处在最尾，因为有循环，所以根本不影响。不理解的老铁还是同样的，画图加深理解。

 

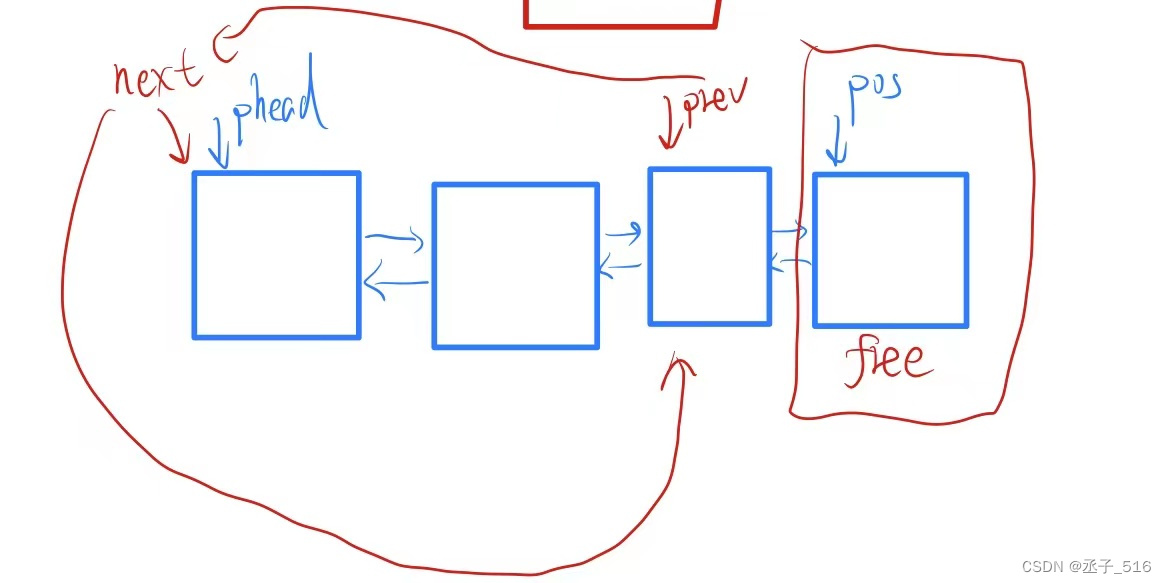
//删除
void listerase(listnode* pos)
{
	assert(pos);
	listnode* prev = pos->prev;
	listnode* next = pos->next;
	prev->next = next;
	next->prev = prev;
	free(pos);
}

到这里，双向循环链表的增删查改就介绍完毕了。是不是很简单呢？

虽然结构复杂，但其功能的实现却方便快捷，书写难度低，同时通过定义俩指针，就不用考虑指针的指向修改顺序，无脑改就完了。而且因为有循环，所以对空链表，或者对尾处理等操作就不像单向链表需要考虑更多的情况了。

但是代码仍然可以优化。代码复用嘛。

因为我们写的代码很多地方其实是重复的。所以可以对一些函数进行更改。

例如

尾删替换为

listerase(phead->prev);

头删替换为

listerase(phead->next);

头插和尾插呢？

一样嘛，将pos的位置进行改变就行了。

头插

listnode* pos=phead->next;
listinsert(pos,x);

尾插

listinsert(phead, x);

剩下的就是destory，定义一个cur和next，cur指向第一个节点，next指向cur的next，free掉cur，再将cur=next，不断循环即可。这里就不贴出代码了，感兴趣的老铁试着自己书写下。

记得phead也要释放哦。

这样我们就做成了一个功能齐全且代码维护方便的链表。可以被称作很优秀的结构了。除了查找的时间复杂度是O（N）外，其他一切都很完美。

但是查找我们也不用链表来使用，而是平衡搜索树，哈希表，b树，这样的非常复杂的结构，感兴趣的老铁自行度娘吧。

3.链表相关oj题（来源leetcode）

3.1反转链表（笔试常考）

例如 1-》2-》3-》4

反转 4-》3-》2-》1

思路1：将指针的方向反一圈

定义三指针。两个指针的功能是反转指针，还有一个拿来存储下一个需要反转的地址，不然两个指针反转完了会找不到下一个地址。

然后不断的重复。

#include<stdio.h>
struct listnode* reverse(struct listnode* head)
{
	if (head == NULL)   //针对空链表的处理。
	{
		return NULL;
	}
	struct listnode* n1 = NULL;
	struct listnode* n2 = head;
	struct listnode* n3 = n2->next;  //如果是空链表，n2的next会出错。
	
	while (n2)
	{
		n2->next = n1;
		n1 = n2;
		n2 = n3;
		if (n3)  //n3可能为空，那么n3的next也就会报错
		{
			n3 = n3->next;
		}
	}
	//链表的头换成了n1
	return n1;
 
}

在做单向链表时请一定小心各种->next,因为他很有可能为空。

思路2：头插法

用头插法来插123，就会得到321了

所以就是取原链表的节点头插到新链表里去。

定义俩指针，一个保存头插过后的下一个节点的地址。一个取节点去新链表头插。

struct listnode* reverse(struct listnode* head)
{
	struct listnode* cur = head;
	struct listnode* newhead = NULL;
	while (cur)
	{
		struct listnode* next = cur->next;
		cur->next = newhead;
		newhead = cur;//将newhead当作新的头
		cur = next;
	}
	return newhead;
}

3.2查找链表的中间节点

给一个头节点为head的非空单链表，返回其中间结点。

若有两个，则返回第二个。

要求：只可以遍历一遍

思路：定义两个指针，fast与slow，如其名，对其速度有所要求，slow走一步，fast走两步。

当fast走到尾指针时，slow就走到了中间。但是需要区别下偶数和奇数的节点的链表，会发现是有细微的差别的。偶数时，fast指向了链表最后一个，而奇数时，fast走向了空。

struct listnode* middlenode(struct listnode* head)
{
	struct listnode* slow = head;
	struct listnode* fast= head;
	while (fast && fast->next )//有一个为空就停止。
	{
		slow = slow->next;
		fast = fast->next->next;
	}
	return slow;
}

3.3合并两个有序链表

将两个升序的链表合并为新升序链表，新链表由旧节点组成。

思路：从头开始，取两链表中小的尾插到新链表。

和以前讲的一道题很类似，分别定义俩指针，指向两个链表，不断的比较插入。不过需要改变的是可以给新链表附加一个head和tail，方便找到嘛。tail就随着插入不断的向后移。当一个链表的指针指向空，就结束，将另一个剩下的拼接到新的后面。

struct listnode* mergetwolists(struct listnode* l1, struct listnode* l2)
{
	if (l1 == NULL)
	{
		return l2;
	}
	if (l2 == NULL)
	{
		return l1;
	}
	struct listnode* head = NULL;
	struct listnode* tail = NULL;
	while (l1 != NULL && l2 != NULL)  // 一个结束就都结束了
	{
		if (l1->val < l2->val) //val是题给的值，相当于上文讲的data
		{
			if (tail == NULL)
			{
				head = tail = l1;
			}
			else
			{
				tail->next = l1;
				tail = tail->next;
			}
			l1 = l1->next;
		}
		else
		{
			if (tail == NULL)
			{
				head = tail = l2;
			}
			else
			{
				tail->next = l2;
				tail = tail->next;
			}
			l2 = l2->next;
		}
	}
	if (l1 != NULL)
	{
		tail->next = l1;
	}
	if (l2 != NULL)
	{
		tail->next = l2;
	}
	
}

3.4环形链表（较难）

给你一个链表的头节点 head ，判断链表中是否有环。

如果链表中有某个节点，可以通过连续跟踪 next 指针再次到达，则链表中存在环。 为了表示给定链表中的环，评测系统内部使用整数 pos 来表示链表尾连接到链表中的位置（索引从 0 开始）。注意：pos 不作为参数进行传递 。仅仅是为了标识链表的实际情况。

如果链表中存在环 ，则返回 true 。 否则，返回 false 。

示例 1：

输入：head = [3,2,0,-4], pos = 1
输出：true
解释：链表中有一个环，其尾部连接到第二个节点。
示例 2：

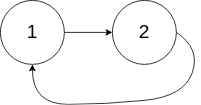
输入：head = [1,2], pos = 0
输出：true
解释：链表中有一个环，其尾部连接到第一个节点。
示例 3：

输入：head = [1], pos = -1
输出：false
解释：链表中没有环。

思路：仍然使用fast与slow指针，fast会比slow更快进环，当两个指针都进环，在某个点相遇，不带环则快指针会更快出去。

bool hasCycle(struct ListNode *head) {
    struct ListNode* slow =head, *fast=head;
    while(fast && fast->next)
    {
        slow=slow->next;
        fast=fast->next->next;
        if(slow==fast)
        {
            return true;
        }
        
    }
    return false;
}

思考：slow和fast一定会在环里相遇吗？

假设slow走一步，fast走两步，slow开始进环，fast开始追逐， 若距离为n，则在追逐的过程中距离该如何变化呢？

n，n-1，n-2，n-3，n-4，````0，其距离会越来越小，所以一定会相遇。

若fast走3步呢？

n，n-2，n-4，n-6`````，不一定会被减到0。

n是偶数，就会最终相遇，而n为奇数，就会得到-1，fast比slow还快了一步。

那么，此时他们的距离就是环长-1，若环长-1等于偶数，则可以追上，若是奇数，那就永远追不上了。因为距离被永久定位了环长-1了。

奇数意味着快追上时，fast又会反超slow。

若fast走4步？走5步？感兴趣的铁子自行证明一下。