MIT | 数据分析、信号处理和机器学习中的矩阵方法 笔记系列 Lecture 2: Multiplying and Factoring Matrices_gilbert strang数据分析、信号处理和机器学习中的矩阵方法

MIT | 数据分析、信号处理和机器学习中的矩阵方法

本系列为MIT Gilbert Strang教授的"数据分析、信号处理和机器学习中的矩阵方法"的学习笔记。

• Gilbert Strang & Sarah Hansen | Spring 2018
• 18.065: Matrix Methods in Data Analysis, Signal Processing, and Machine Learning
• 视频网址: https://ocw.mit.edu/courses/18-065-matrix-methods-in-data-analysis-signal-processing-and-machine-learning-spring-2018/
• 关注下面的公众号，回复“ 矩阵方法 ”，即可获取 本系列完整的pdf笔记文件~

---

内容在CSDN、知乎和微信公众号同步更新

• CSDN博客
• 知乎
• 微信公众号

• Markdown源文件暂未开源，如有需要可联系邮箱
• 笔记难免存在问题，欢迎联系邮箱指正

---

Lecture 0: Course Introduction

Lecture 1 The Column Space of $A$ Contains All Vectors $Ax$

Lecture 2 Multiplying and Factoring Matrices

Lecture 3 Orthonormal Columns in $Q$ Give $Q^{\prime }Q=I$

Lecture 4 Eigenvalues and Eigenvectors

Lecture 5 Positive Definite and Semidefinite Matrices

Lecture 6 Singular Value Decomposition (SVD)

Lecture 7 Eckart-Young: The Closest Rank $k$ Matrix to $A$

Lecture 8 Norms of Vectors and Matrices

Lecture 9 Four Ways to Solve Least Squares Problems

Lecture 10 Survey of Difficulties with $Ax=b$

Lecture 11 Minimizing ||x|| Subject to $Ax=b$

Lecture 12 Computing Eigenvalues and Singular Values

Lecture 13 Randomized Matrix Multiplication

Lecture 14 Low Rank Changes in $A$ and Its Inverse

Lecture 15 Matrices $A(t)$ Depending on $t$, Derivative = $dA/dt$

Lecture 16 Derivatives of Inverse and Singular Values

Lecture 17 Rapidly Decreasing Singular Values

Lecture 18 Counting Parameters in SVD, LU, QR, Saddle Points

Lecture 19 Saddle Points Continued, Maxmin Principle

Lecture 20 Definitions and Inequalities

Lecture 21 Minimizing a Function Step by Step

Lecture 22 Gradient Descent: Downhill to a Minimum

Lecture 23 Accelerating Gradient Descent (Use Momentum)

Lecture 24 Linear Programming and Two-Person Games

Lecture 25 Stochastic Gradient Descent

Lecture 26 Structure of Neural Nets for Deep Learning

Lecture 27 Backpropagation: Find Partial Derivatives

Lecture 28 Computing in Class [No video available]

Lecture 29 Computing in Class (cont.) [No video available]

Lecture 30 Completing a Rank-One Matrix, Circulants!

Lecture 31 Eigenvectors of Circulant Matrices: Fourier Matrix

Lecture 32 ImageNet is a Convolutional Neural Network (CNN), The Convolution Rule

Lecture 33 Neural Nets and the Learning Function

Lecture 34 Distance Matrices, Procrustes Problem

Lecture 35 Finding Clusters in Graphs

Lecture 36 Alan Edelman and Julia Language

---

目录

---

Lecture 2: Multiplying and Factoring Matrices

2.1 五种矩阵分解

• 矩阵分解的5种类型：(Five Key Factorizations)

  • $A=LU$
  • $A=QR$
  • $S=Q\Lambda Q^T$
  • $A=X\Lambda X^{-1}$
  • $A=U\Sigma V$`

• $A=LU$:

  • 含义：
    • L: lower triangular matrix
    • U: Upper triangular matrix
  • 作用：
    • about elimination, solving linear systems
    • More about elimination:
      • 刚开始学线性代数时，求解$Ax=b$的方法：
        • 通过各种row operation进行求解
          • 线性方程组的初等变换：
            • （1）互换两个方程的位置
            • （2）用一个非零数乘以某一个方程
            • （3）把一个方程的倍数加到另一个方程
          • 实质：线性方程组的解的过程实际上就是反复对方程组进行初等变换。
      • "elimination"的含义：
        • $A=LU$ perfectly express those row operations!
  • 为什么叫Elimination？
    • 首先看如何通过elimination进行LU分解？
      • A= $\left[\begin{array}{cc}2& 3\\ 4& 7\end{array}\right]$
      • $\left[\begin{array}{cc}2& 3\\ 4& 7\end{array}\right]\to \left[\begin{array}{cc}2& 3\\ 0& 1\end{array}\right]$
        • $U=\left[\begin{array}{cc}2& 3\\ 0& 1\end{array}\right]$
      • 即可得到L
        • $L=\left[\begin{array}{cc}1& 0\\ 2& 1\end{array}\right]$
      • 完成了LU分解 $A=LU=\left[\begin{array}{cc}1& 0\\ 2& 1\end{array}\right]\left[\begin{array}{cc}2& 3\\ 0& 1\end{array}\right]$
    • Elimination的含义：
      • 本来有很多个无法直接求解的方程
      • 通过LU分解，U矩阵中最后一行只有一个方程需要求解
        • 也就是，如何进行如下分解：?
          • $A=\left[\begin{array}{cc}2& 3\\ 4& 7\end{array}\right]=\left[\begin{array}{cc}2& 3\\ 4& ?\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& ??\end{array}\right]$
          • 且两个矩阵的rank都是1
          • 其实高斯消元本质上也是这么做的
        • 使用LU分解即可：
          • $A=LU=\left[\begin{array}{cc}1& 0\\ 2& 1\end{array}\right]\left[\begin{array}{cc}2& 3\\ 0& 1\end{array}\right]$
            $=\left[\begin{array}{cc}2& 3\\ 4& 6\end{array}\right]+\left[\begin{array}{cc}0& 0\\ 0& 1\end{array}\right]$
      • 高斯消元 $\to$ “Elimination”
        • peel off 剥去，脱掉
  • 分解条件：
    • 如果一个秩为k的矩阵A的前k个顺序主子式不为零，那么它就可以进行LU分解

• $A=QR$

  • Gram-Schmidt
  • Least squares is the big application
  • Q: Orthogonal Orthogonal 正交的
    • The columns are orthogonal
      • means they are perpendicular perpendicular 垂直的 to each other
    • often orthonormal orthonormal 标准正交的
      • means they are unit vectors and orthogonal
  • R: 上三角矩阵

• $S=Q\Lambda Q^T$

  • really a central one in math!
    • in pure math/ applied math/ etc.
  • 具体含义：
    • S: symmetric matrix
      • $S=Q\Lambda Q^T$ is a special factorization for symmetric matrix
    • $\Lambda$: the diagonal eigenvalue matrix
    • $Q$: 也是orthonormal matrix，但由eigenvectors组成
      • 需要额外的工作去计算特征向量才能得到
      • 而不像QR分解中可直接通过施密特正交化得到
  • 对称矩阵的性质
    • 展开后：
      • $S=Q\Lambda Q^T=\left[\begin{array}{cccc}{q}_1& q_2& \cdot \cdot \cdot & q_n\end{array}\right]\left[\begin{array}{cccc}{\lambda }_1& 0& \cdot \cdot \cdot & 0\\ 0& {\lambda }_2& \cdot \cdot \cdot & 0\\ \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot & \cdot \cdot \cdot \\ 0& 0& \cdot \cdot \cdot & {\lambda }_n\end{array}\right]\left[\begin{array}{c}{q}_1^T\\ q_2^T\\ \cdot \cdot \cdot \\ q_n^T\end{array}\right]$
      • 其中$q$为特征向量(列向量)
      • 结论1：The eigenvectors are orthogonal (For 对称矩阵)
        • 全部n个特征向量
      • 结论2：The eigenvalues are real (For 对称矩阵)
  • 作用1：矩阵乘法
    • $Q\Lambda Q^T=(Q\Lambda )Q^T$
    • The columns of $(Q\Lambda )$ $\times$ rows of $Q^T$
      • 注意：这样矩阵乘法中的 每一个piece矩阵(一列与一行的乘积)的rank都是1！
        • all columns 都是那一列的multiples
        • all rows 都是那一行的multiples
        • e.g., $\left[\begin{array}{c}1\\ 2\end{array}\right]\left[\begin{array}{cc}3& 4\end{array}\right]=\left[\begin{array}{cc}3& 4\\ 6& 8\end{array}\right]$
    • 因此：$(Q\Lambda )Q^T$ is the sum of rank 1 matrices
      • 第一个rank 1 matrix:
        • $(Q\Lambda )$的第一列：${\lambda }_1{q}_1$
        • $Q^T$的第一行: $q_1^T$
        • 矩阵: ${\lambda }_1{q}_1{q}_1^T$
    • 最终结果：$S=Q\Lambda Q^T=(Q\Lambda )Q^T={\lambda }_1{q}_1{q}_1^T+{\lambda }_2{q}_2{q}_2^T+\cdot \cdot \cdot +{\lambda }_n{q}_n{q}_n^T$
      • 相当于 把S分解为了n个rank 1 pieces
      • 而且这里每个piece还很特殊
        • 都是symmetric
        • ${\lambda }_n{q}_n{q}_n^T$是对称的
    • 验证上述结果：
      • Look at $S{q}_1$
        • $S{q}_1={\lambda }_1{q}_1{q}_1^T{q}_1+{\lambda }_2{q}_2{q}_2^T{q}_1+...+{\lambda }_n{q}_n{q}_n^T{q}_1$
        • 因为$Q$是标准正交阵：
          • $S{q}_1={\lambda }_1{q}_1\Vert q_1{\Vert }^2={\lambda }_1{q}_1$
    • 结果正确：$S{q}_1={\lambda }_1{q}_1$
      • 符合the definitions of eigenvalues and eigenvectors

• $A=U\Sigma V$

  • 奇异值分解 (SVD)
    • Singular Value Decomposition
    • a foundational factorization for this course and for all of data science
  • 含义：
    • U: an orthogonal matrix
    • V: an orthogonal matrix
    • $\Sigma$: a diagonal matrix
  • 意义：
    • It works for every matrix
      • Rectangular matrix
      • has enough eigenvectors or not
      • 但其他的分解，比如$A=X\Lambda X^{-1}$就不行，原因：
        • SVD的U和V是两个不同的orth. 矩阵
          • two different sets of singular vectors
        • 而$A=X\Lambda X^{-1}$中X只代表了一个set

5.2 Four sub-spaces in linear algebra

• about 4 fundamental sub spaces for matrix A
  • 1 Column space $C(A)$
    • dim = r $(r\le n)$
  • 2 Row Space $C(A^T)$
    • dim = r $(r\le n)$
    • dim of $C(A)$ = dim of $C(A^T)$ 是lecture 1的重要结论
  • 3 Null Space $N(A)$
    • null space = all solutions $x$ to $Ax=0$
    • "null"的含义： reflecting the fact that that’s a zero (Ax = 0)
    • How many independent vectors in the null space (N(A)的维度是多少)
      • $dim=n-r$
        • 有n个unkowns (未知数)
        • r个constraints
        • 因此Null space的维度为$n-r$
  • 4 Null Space of $A^T$ $N(A^T)$

---

• What is implied when I say the “sapce” of vectors?
  • “space”: means I can do the most important operations of linear algebra in that space
    • 事实上，向量空间本来就和群环域在概念上有很大关联
      • 给定域F，向量空间V记为F-向量空间。其二元运算：
      • 向量加法：+ : V × V → V 记作 v + w, ∃ v, w ∈ V
      • 标量乘法：·: F × V → V 记作 a v, ∃a ∈ F 且 v ∈ V
      • 并且满足如下8条公理 [根据百科]：
        • 向量加法结合律：u + (v + w) = (u + v) + w
        • 向量加法的单位元：V存在零向量的0，∀ v ∈ V , v + 0 = v
        • 向量加法的逆元素：∀v∈V, ∃w∈V，使得 v + w = 0
        • 向量加法交换律：v + w = w + v
        • 标量乘法与域乘法兼容性(compatibility): a(b v) = (ab)v
        • 标量乘法有单位元: 1 v = v, 1指域F的乘法单位元
        • 标量乘法对于向量加法满足分配律：a(v + w) = a v + a w
        • 标量乘法对于域加法满足分配律: (a + b)v = a v + b v
      • 例如：
        • Given Ax = 0 and Ay = 0, then A(x+y) = 0:
          • 若$x,y\in N(A)$, then x+y $\in N(A)$
      • 正是这些性质，使线性代数成为可能
        • can take linear combinations
        • if I take combinations of two null space guys, I am still in the null space
    • 除了向量空间外，还有模(module)的概念:

      • A module over a ring is a generalization of the notion of vector space over a field, wherein the corresponding scalars are the elements of an arbitrary ring.

---

• 这四个subspaces之间的关系
  • 如下图
  • 对于矩阵$A(m\times n)$
    • Two spaces are in $R^n$
      • Row space $C(A^T)$
        • $dim=r$
      • Null space $N(A)$
        • $dim=n-r$
      • 二者dim相加恰好为n
        • 意味着： Every vector has a piece in the row space, and a piece in the null space
          • and those two pieces give you back the vector
          • 解释见 subspaces relationship
    • Two spaces are in $R^m$
      • Column Space $C(A)$
        • $dim=r$
      • Null space of $A^T$: $N(A^T)$
        • $dim=m-r$

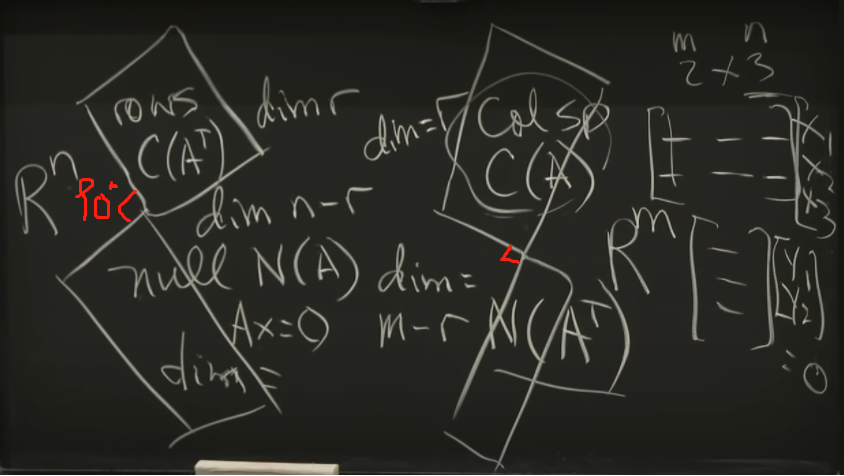
• 下一个问题：$C(A^T)$是$R^n$中一个r dimensional plane, $N(A)$是$R^n$中一个(n-r) dimensional plane, 那么 How are those two planes connected?
  • row space:
    • $A^{T}y$ for $\forall y$
    • dim r
  • Null space:
    • $x$ for $Ax=0$
    • dim n-r
  • an example
    • $A=\left[\begin{array}{ccc}1& 2& 4\\ 2& 4& 8\end{array}\right]$
    • m = 2; n = 3; r = 1
    • 先看Null space:
      • n - r =2: 所以应该能够找到两个independent vectors $x_1$ and $x_2$, s.t., $A{x}_1=A{x}_2=0$
        • 例如$x_1=[0,-2,1{]}^T$; $x_2=[4,0,-1{]}^T$
    • 再看 Row Space:
      • 比如A的第一行 $x_r=[1,2,4]$
    • 它们有什么关系？？
      • Orthogonal!
  • 结论: Null space 与 Row Space正交！
    • 这也是之前所说的 Every vector has a piece in the row space, and a piece in the null space的含义
  • 意义：
    • a completely general fact
    • 凡是满足$Ax=0$的$x$, 一定和$A$的rows及其combinations正交
      • When I look at $Ax=0$, it is telling me that x is orthogonal to the row
      • 这也符合常识
    • This is the fundamental theorem of linear algebra to see that the dimensions come out right, and the geometry comes out right.

Next lecture:

• move on quickly to eigenvalues and positive definite matrices