栈及其应用_栈的应用

作者：一键难忘520 | 2024-07-23 08:23:52

踩

栈的应用

栈

1、定义

栈是一个先入后出的有序列表
栈(stack)是限制线性表中元素的插入和删除只能在线性表的同一端进行的一种特殊线性表。允许插入和删除的一端，为变化的一端，称为栈顶(Top)，另一端为固定的一端，称为栈底(Bottom)。
最先放入的元素在栈底，且最后出栈。最后放入的元素在栈顶，且最先出栈
解方式说明出栈(pop)和入栈(push)的概念

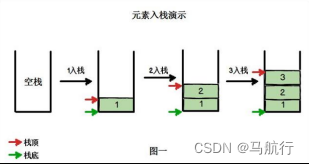
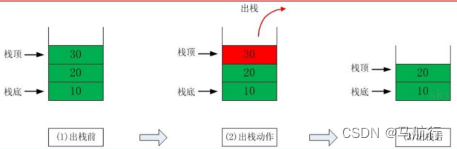
2、应用场景

子程序递归调用。如JVM中的虚拟机栈
表达式转换（中缀转后缀）与求值
二叉树的遍历
图的深度优先遍历

3、实现

用数组模拟实现

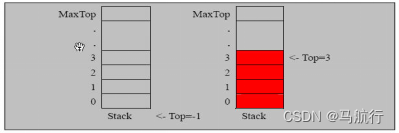
在这里插入图片描述
思路：

定义一个 top 来表示栈顶，初始化为 -1
入栈的操作，当有数据加入到栈时， top++; stack[top] = data
出栈的操作， int value = stack[top]; top–, return value
根据定义，top == -1时，栈空
top == maxSize-1时，栈满
代码如下：

import java.util.Scanner;
public class ArrayStackDemo {

	public static void main(String[] args) {

		//先创建一个ArrayStack对象->表示栈
		ArrayStack stack = new ArrayStack(4);
		String key = "";
		boolean loop = true; //控制是否退出菜单
		Scanner scanner = new Scanner(System.in);
		
		while(loop) {
			System.out.println("show: 表示显示栈");
			System.out.println("exit: 退出程序");
			System.out.println("push: 表示添加数据到栈(入栈)");
			System.out.println("pop: 表示从栈取出数据(出栈)");
			System.out.println("请输入你的选择");
			key = scanner.next();
			switch (key) {
			case "show":
				stack.list();
				break;
			case "push":
				System.out.println("请输入一个数");
				int value = scanner.nextInt();
				stack.push(value);
				break;
			case "pop":
				try {
					int res = stack.pop();
					System.out.printf("出栈的数据是 %d\n", res);
				} catch (Exception e) {
					// TODO: handle exception
					System.out.println(e.getMessage());
				}
				break;
			case "exit":
				scanner.close();
				loop = false;
				break;
			default:
				break;
			}
		}
		
		System.out.println("程序退出~~~");
	}

}

//定义一个 ArrayStack 表示栈
class ArrayStack {
	private int maxSize; // 栈的大小
	private int[] stack; // 数组，数组模拟栈，数据就放在该数组
	private int top = -1;// top表示栈顶，初始化为-1
	
	//构造器
	public ArrayStack(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//栈满
	public boolean isFull() {
		return top == maxSize - 1;
	}
	//栈空
	public boolean isEmpty() {
		return top == -1;
	}
	//入栈-push
	public void push(int value) {
		//先判断栈是否满
		if(isFull()) {
			System.out.println("栈满");
			return;
		}
		top++;
		stack[top] = value;
	}
	//出栈-pop, 将栈顶的数据返回
	public int pop() {
		//先判断栈是否空
		if(isEmpty()) {
			//抛出异常
			throw new RuntimeException("栈空，没有数据~");
		}
		int value = stack[top];
		top--;
		return value;
	}
	//显示栈的情况[遍历栈]， 遍历时，需要从栈顶开始显示数据
	public void list() {
		if(isEmpty()) {
			System.out.println("栈空，没有数据~~");
			return;
		}
		//需要从栈顶开始显示数据
		for(int i = top; i >= 0 ; i--) {
			System.out.printf("stack[%d]=%d\n", i, stack[i]);
		}
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105

4.应用

1.中缀表达式计算（表达式求值）
思路：
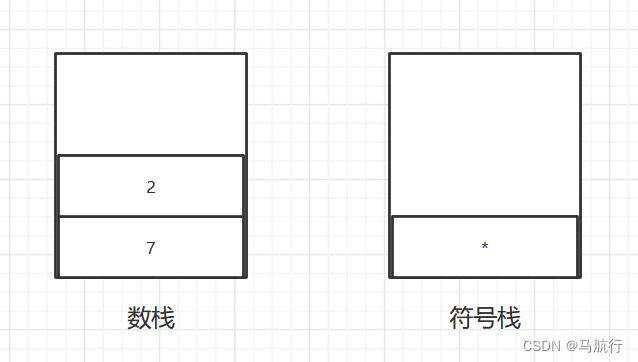
请添加图片描述

通过一个 index 值（索引），来遍历我们的表达式(字符串)
如果我们发现是一个数字, 就直接入数栈
如果发现扫描到是一个符号, 就分如下情况
3.1. 如果发现当前的符号栈为空，就直接入栈
3.2.如果符号栈有操作符，就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符，就需要从数栈中pop出两个数,在从符号栈中pop出一个符号，进行运算，将得到结果，入数栈，然后将当前的操作符入符号栈，如果当前的操作符的优先级大于栈中的操作符，就直接入符号栈.
当表达式扫描完毕，就顺序的从数栈和符号栈中pop出相应的数和符号，并运行.
最后在数栈只有一个数字，就是表达式的结果

代码如下：

import java.util.Scanner;

public class Calculator {

	public static void main(String[] args) {
		//根据前面老师思路，完成表达式的运算
		//创建两个栈，数栈，一个符号栈
		System.out.println("请输入表达式：");
		Scanner scanner = new Scanner(System.in);
		String expression = scanner.next();
		ArrayStack2 numStack = new ArrayStack2(10);
		ArrayStack2 operStack = new ArrayStack2(10);
		//定义需要的相关变量
		int index = 0;//用于扫描
		int num1 = 0; 
		int num2 = 0;
		int oper = 0;
		int res = 0;
		char ch = ' '; //将每次扫描得到char保存到ch
		String keepNum = ""; //用于拼接 多位数
		//开始while循环的扫描expression
		while(true) {
			//依次得到expression 的每一个字符
			ch = expression.substring(index, index+1).charAt(0);
			//判断ch是什么，然后做相应的处理
			if(operStack.isOper(ch)) {//如果是运算符
				//判断当前的符号栈是否为空
				if(!operStack.isEmpty()) {
					//如果符号栈有操作符，就进行比较,如果当前的操作符的优先级小于或者等于栈中的操作符,就需要从数栈中pop出两个数,
					//在从符号栈中pop出一个符号，进行运算，将得到结果，入数栈，然后将当前的操作符入符号栈
					if(operStack.priority(ch) <= operStack.priority(operStack.peek())) {
						num1 = numStack.pop();
						num2 = numStack.pop();
						oper = operStack.pop();
						res = numStack.cal(num1, num2, oper);
						//把运算的结果如数栈
						numStack.push(res);
						//然后将当前的操作符入符号栈
						operStack.push(ch);
					} else {
						//如果当前的操作符的优先级大于栈中的操作符， 就直接入符号栈.
						operStack.push(ch);
					}
				}else {
					//如果为空直接入符号栈..
					operStack.push(ch); // 1 + 3
				}
			} else { //如果是数，则直接入数栈
				
				//numStack.push(ch - 48); //? "1+3" '1' => 1
				//分析思路
				//1. 当处理多位数时，不能发现是一个数就立即入栈，因为他可能是多位数
				//2. 在处理数，需要向expression的表达式的index 后再看一位,如果是数就进行扫描，如果是符号才入栈
				//3. 因此我们需要定义一个变量 字符串，用于拼接
				
				//处理多位数
				keepNum += ch;
				
				//如果ch已经是expression的最后一位，就直接入栈
				if (index == expression.length() - 1) {
					numStack.push(Integer.parseInt(keepNum));
				}else{
				
					//判断下一个字符是不是数字，如果是数字，就继续扫描，如果是运算符，则入栈
					//注意是看后一位，不是index++
					if (operStack.isOper(expression.substring(index+1,index+2).charAt(0))) {
						//如果后一位是运算符，则入栈 keepNum = "1" 或者 "123"
						numStack.push(Integer.parseInt(keepNum));
						//重要的!!!!!!, keepNum清空
						keepNum = "";
						
					}
				}
			}
			//让index + 1, 并判断是否扫描到expression最后.
			index++;
			if (index >= expression.length()) {
				break;
			}
		}
		
		//当表达式扫描完毕，就顺序的从 数栈和符号栈中pop出相应的数和符号，并运行.
		while(true) {
			//如果符号栈为空，则计算到最后的结果, 数栈中只有一个数字【结果】
			if(operStack.isEmpty()) {
				break;
			}
			num1 = numStack.pop();
			num2 = numStack.pop();
			oper = operStack.pop();
			res = numStack.cal(num1, num2, oper);
			numStack.push(res);//入栈
		}
		//将数栈的最后数，pop出，就是结果
		int res2 = numStack.pop();
		System.out.printf("表达式 %s = %d", expression, res2);
	}

}

//先创建一个栈,直接使用前面创建好
//定义一个 ArrayStack2 表示栈, 需要扩展功能
class ArrayStack2 {
	private int maxSize; // 栈的大小
	private int[] stack; // 数组，数组模拟栈，数据就放在该数组
	private int top = -1;// top表示栈顶，初始化为-1
	
	//构造器
	public ArrayStack2(int maxSize) {
		this.maxSize = maxSize;
		stack = new int[this.maxSize];
	}
	
	//增加一个方法，可以返回当前栈顶的值, 但是不是真正的pop
	public int peek() {
		return stack[top];
	}
	
	//栈满
	public boolean isFull() {
		return top == maxSize - 1;
	}
	//栈空
	public boolean isEmpty() {
		return top == -1;
	}
	//入栈-push
	public void push(int value) {
		//先判断栈是否满
		if(isFull()) {
			System.out.println("栈满");
			return;
		}
		top++;
		stack[top] = value;
	}
	//出栈-pop, 将栈顶的数据返回
	public int pop() {
		//先判断栈是否空
		if(isEmpty()) {
			//抛出异常
			throw new RuntimeException("栈空，没有数据~");
		}
		int value = stack[top];
		top--;
		return value;
	}
	//显示栈的情况[遍历栈]， 遍历时，需要从栈顶开始显示数据
	public void list() {
		if(isEmpty()) {
			System.out.println("栈空，没有数据~~");
			return;
		}
		//需要从栈顶开始显示数据
		for(int i = top; i >= 0 ; i--) {
			System.out.printf("stack[%d]=%d\n", i, stack[i]);
		}
	}
	//返回运算符的优先级，优先级是程序员来确定, 优先级使用数字表示
	//数字越大，则优先级就越高.
	public int priority(int oper) {
		if(oper == '*' || oper == '/'){
			return 1;
		} else if (oper == '+' || oper == '-') {
			return 0;
		} else {
			return -1; // 假定目前的表达式只有 +, - , * , /
		}
	}
	//判断是不是一个运算符
	public boolean isOper(char val) {
		return val == '+' || val == '-' || val == '*' || val == '/';
	}
	//计算方法
	public int cal(int num1, int num2, int oper) {
		int res = 0; // res 用于存放计算的结果
		switch (oper) {
		case '+':
			res = num1 + num2;
			break;
		case '-':
			res = num2 - num1;// 注意顺序
			break;
		case '*':
			res = num1 * num2;
			break;
		case '/':
			res = num2 / num1;
			break;
		default:
			break;
		}
		return res;
	}
	
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197

注意细节：1.没处理空格 2.多位数的处理 3.因为栈是用的整型数组，所以计算除法的时候，无法转化成double

2.中缀转后缀(也叫逆波兰)

后缀表达式运算方法

从左向右读取表达式
- 遇到数字就压入栈中
- 遇到运算符就弹出栈顶和次顶元素。用次顶元素运算符栈顶元素，并将运算结果压入栈中，直到栈为空，最终结果就是运算结果

大家看到，后缀表达式适合计算机进行运算，但是人却不太容易写出来，尤其是表达式很长的情况下，因此在开发中，我们需要将中缀表达式转成后缀表达式

具体步骤如下：

初始化两个栈：运算符栈 s1 和储存中间结果的栈 s2；
从左至右扫描中缀表达式
遇到操作数时，将其压 s2；
遇到运算符时，比较其与 s1 栈顶运算符的优先级
- 如果 s1 为空，或栈顶运算符为左括号“(”，则直接将此运算符入栈；
- .否则，若优先级比栈顶运算符的高，也将运算符压入 s1
- 否则，将 s1 栈顶的运算符弹出并压入到 s2 中，再次转到(4-1)与 s1 中新的栈顶运算符相比较；
遇到括号时
- 如果是左括号“(”，则直接压入 s1
- 如果是右括号“)”，则依次弹出 s1 栈顶的运算符，并压入 s2，直到遇到左括号为止，此时将这一对括号丢弃
重复步骤 2 至 5，直到表达式的最右边
将 s1 中剩余的运算符依次弹出并压入 s2
依次弹出 s2 中的元素并输出，结果的逆序即为中缀表达式对应的后缀表达式
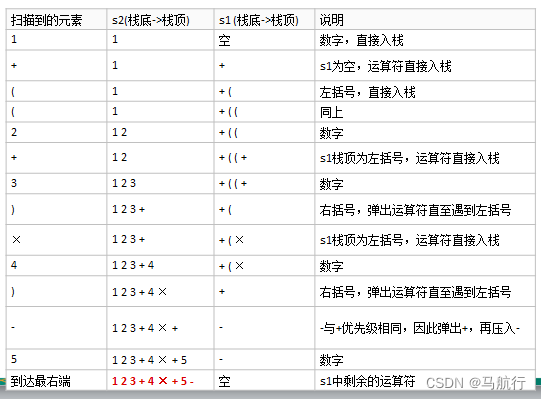
例如：将中缀表达式“1+((2+3)×4)-5”转换为后缀表达式的过程如下
因此结果为 :"1 2 3 + 4 × + 5 –

在这里插入图片描述
代码：

public class Demo4 {
   static Queue<String> queue = new LinkedList<>();
   static Stack<String> stack = new Stack<>();

   public static void main(String[] args) {
      //中缀表达式，加上空格，方便取出
      String infixExpression = "1 + ( ( 2 + 3 ) * 4 ) - 5";
      String[] expressionArr = infixExpression.split(" ");
      //用来保存该运算符的类型
      int type;
      //取出的字符串
      String element;
      //弹出栈的字符串
      String stackEle;
      for(int i=0; i<expressionArr.length; i++) {
         element = expressionArr[i];
         type = judgeOperator(element);
         if(type == 0) {
            //数字，直接入队
            queue.add(element);
         }else if(type == 1) {
            //左括号，直接压栈
            stack.push(element);
         }else if(type == 3) {
            //如果右括号，弹出栈顶元素，直到遇见左括号位置再停下来
            do {
               stackEle = stack.pop();
               if(stackEle.equals("(")) {
                  break;
               }
               queue.add(stackEle);
               //弹出栈中的左括号
            }while (!stackEle.equals("("));
         }else if(type == 2) {
            if(stack.isEmpty()) {
               //如果栈为空，直接入栈
               stack.push(element);
               continue;
            }
            int priority1 = getPriority(element);
            //获得栈顶元素，并判断其优先级
            stackEle = stack.peek();
            int priority2 = getPriority(stackEle);
            if(priority2 == 0) {
               //为左括号，运算符直接入栈
               stack.push(element);
            }else if(priority1 > priority2) {
               //该运算符优先级高于栈顶元素优先级，则入栈
               stack.push(element);
            }else {
               stackEle = stack.pop();
               queue.add(stackEle);
               //重新判断该运算符
               i--;
            }
         }
      }
      //把最后一个元素出栈并入队
      stackEle = stack.pop();
      queue.add(stackEle);
      //保存队列长度，因为出队过程中队列的长度会被改变
      int length = queue.size();
      for(int i=0; i<length; i++) {
         element = queue.remove();
         System.out.print(element);
      }
   }

   /**
    * 判断该运算符是不是加减乘除
    * @param operation 运算符
    * @return true则该运算符为加减乘除
    */
   public static boolean firstJudge(String operation) {
      return operation.equals("*") || operation.equals("/") || operation.equals("+") || operation.equals("-");
   }


   /**
    * 判断该字符串的类型
    * @param operation 要判断的字符串
    * @return 3->右括号 2->加减乘除运算符 1->左括号
    */
   public static int judgeOperator(String operation) {
      if(operation.equals(")")) {
         return 3;
      }
      if(firstJudge(operation)) {
         return 2;
      }
      if(operation.equals("(")) {
         return 1;
      } else {
         return 0;
      }
   }

   /**
    * 判断运算符优先级
    * @param operator 要判断的运算符
    * @return 2代表乘除，1代表加减，0代表左括号
    */
   public static int getPriority(String operator) {
      if(operator.equals("*") || operator.equals("/")) {
         return 2;
      }else if(operator.equals("+") || operator.equals("-")) {
         return 1;
      } else {
         return 0;
      }

   }
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113

递归

1、概念
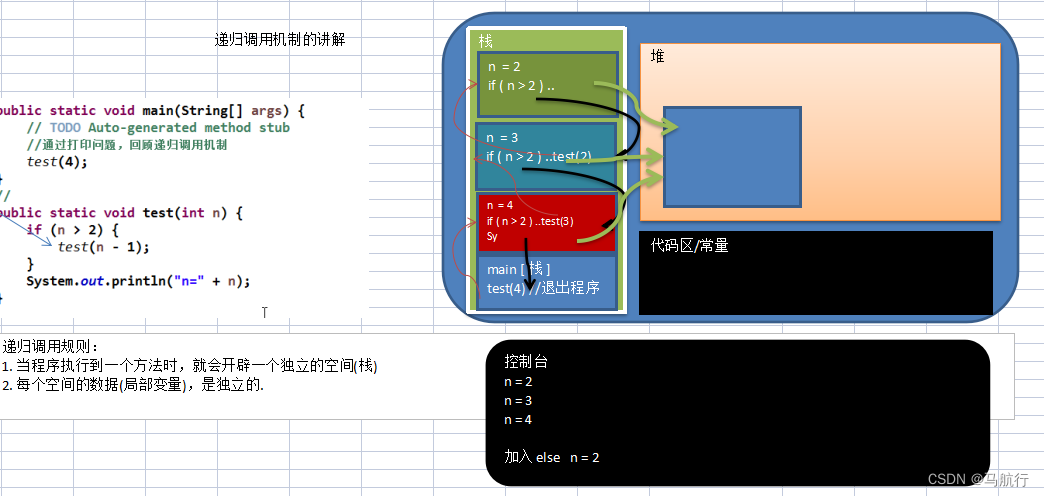
递归就是方法自己调用自己,每次调用时传入不同的变量.递归有助于编程者解决复杂的问题,同时可以让代码变得简洁。并且递归用到了虚拟机栈
在这里插入图片描述
2、能解决的问题

八皇后问题
汉诺塔
求阶乘
迷宫问题
球和篮子
各种排序算法

3、规则

方法的变量是独立的，不会相互影响的
如果方法中使用的是引用类型变量(比如数组)，就会共享该引用类型的数据
递归必须向退出递归的条件逼近，否则就是无限递归，出现 StackOverflowError
当一个方法执行完毕，或者遇到 return，就会返回，遵守谁调用，就将结果返回给谁，同时当方法执行完毕或

者返回时，该方法也就执行完毕

4、迷宫问题

思路：

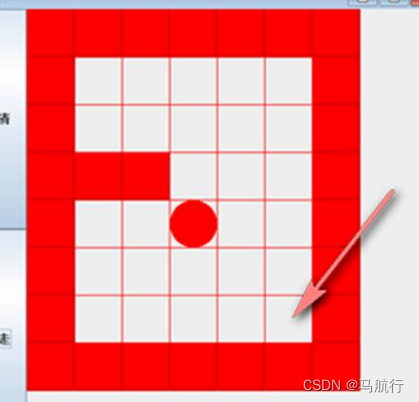
用一个二维矩阵代表地图
- 1代表边界
- 0代表未做过该地点
- 2代表走过且能走得通
- 3代表走过但走不通
设置起点和终点以及每个地点的行走策略
- 行走策略指在该点所走的方向的顺序，如右->下->左->上（调用寻找路径的方法，使用递归）
每次行走时假设该点能够走通，然后按照策略去判断，如果所有策略判断后都走不通，则该点走不通

在这里插入图片描述
代码如下：

package com.atguigu.recursion;

public class MiGong {

	public static void main(String[] args) {
		// 先创建一个二维数组，模拟迷宫
		// 地图
		int[][] map = new int[8][7];
		// 使用1 表示墙
		// 上下全部置为1
		for (int i = 0; i < 7; i++) {
			map[0][i] = 1;
			map[7][i] = 1;
		}

		// 左右全部置为1
		for (int i = 0; i < 8; i++) {
			map[i][0] = 1;
			map[i][6] = 1;
		}
		//设置挡板, 1 表示
		map[3][1] = 1;
		map[3][2] = 1;
//		map[1][2] = 1;
//		map[2][2] = 1;
		
		// 输出地图
		System.out.println("地图的情况");
		for (int i = 0; i < 8; i++) {
			for (int j = 0; j < 7; j++) {
				System.out.print(map[i][j] + " ");
			}
			System.out.println();
		}
		
		//使用递归回溯给小球找路
		//setWay(map, 1, 1);
		setWay2(map, 1, 1);
		
		//输出新的地图, 小球走过，并标识过的递归
		System.out.println("小球走过，并标识过的 地图的情况");
		for (int i = 0; i < 8; i++) {
			for (int j = 0; j < 7; j++) {
				System.out.print(map[i][j] + " ");
			}
			System.out.println();
		}
		
	}
	
	//使用递归回溯来给小球找路
	//说明
	//1. map 表示地图
	//2. i,j 表示从地图的哪个位置开始出发 (1,1)
	//3. 如果小球能到 map[6][5] 位置，则说明通路找到.
	//4. 约定： 当map[i][j] 为 0 表示该点没有走过 当为 1 表示墙  ； 2 表示通路可以走 ； 3 表示该点已经走过，但是走不通
	//5. 在走迷宫时，需要确定一个策略(方法) 下->右->上->左 , 如果该点走不通，再回溯
	/**
	 * 
	 * @param map 表示地图
	 * @param i 从哪个位置开始找
	 * @param j 
	 * @return 如果找到通路，就返回true, 否则返回false
	 */
	public static boolean setWay(int[][] map, int i, int j) {
		if(map[6][5] == 2) { // 通路已经找到ok
			return true;
		} else {
			if(map[i][j] == 0) { //如果当前这个点还没有走过
				//按照策略 下->右->上->左  走
				map[i][j] = 2; // 假定该点是可以走通.
				if(setWay(map, i+1, j)) {//向下走
					return true;
				} else if (setWay(map, i, j+1)) { //向右走
					return true;
				} else if (setWay(map, i-1, j)) { //向上
					return true;
				} else if (setWay(map, i, j-1)){ // 向左走
					return true;
				} else {
					//说明该点是走不通，是死路
					map[i][j] = 3;
					return false;
				}
			} else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
				return false;
			}
		}
	}
	
	//修改找路的策略，改成 上->右->下->左
	public static boolean setWay2(int[][] map, int i, int j) {
		if(map[6][5] == 2) { // 通路已经找到ok
			return true;
		} else {
			if(map[i][j] == 0) { //如果当前这个点还没有走过
				//按照策略 上->右->下->左
				map[i][j] = 2; // 假定该点是可以走通.
				if(setWay2(map, i-1, j)) {//向上走
					return true;
				} else if (setWay2(map, i, j+1)) { //向右走
					return true;
				} else if (setWay2(map, i+1, j)) { //向下
					return true;
				} else if (setWay2(map, i, j-1)){ // 向左走
					return true;
				} else {
					//说明该点是走不通，是死路
					map[i][j] = 3;
					return false;
				}
			} else { // 如果map[i][j] != 0 , 可能是 1， 2， 3
				return false;
			}
		}
	}

}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/一键难忘520/article/detail/869010