当前位置: article > 正文

数学建模之聚类算法（K-means）_k平均聚类初始聚类中心和最终聚类中心是什么

作者：一键难忘520 | 2024-07-12 06:35:27

踩

k平均聚类初始聚类中心和最终聚类中心是什么

K-means聚类算法

k-means算法以k为参数，把n个对像分成k个簇，使簇内具有较高的相似度，而簇间的相似度较低。

1、随机选择k个点作为初始的棸类中心。

2、对于剩下的点，根据其与棸类中心的距离，将其归入最近的簇。

3、对于每个簇，计算所有点的均值作为新的聚类中心。

4、重复2、3直到棸类中心不再发生改变。

K-means的案例分析

例1：现有1999年全国31个省份城镇居民家庭平均每人全年消费性支出的主要变量数据。

目的：通过聚类，了解1999年各个省份的消费水平在国内的情况。

在jupyter下导入相关包与数据

加载数据, 创建K-means算法实例, 井进行训练, 获得标签。

调用K-Means方法所需参数：

1、n_clusters：用于指定聚类中心的个数。

2、 init：初始聚类中心的初始化方法。

3、 max_iter：最大的迭代次数。

4、一般调用时只用给出n_clusters即可，init默认是 k-means ++ ,

max_iter默认是300。

5、fit_predict()：计算簇中心以及为簇分配序号。

输出标签, 分析结果

将城市按照消费水平分成n_clusters类，消费水平相近的城市聚集在一类中。

expens：聚类中心点的数值加和，也就是平均消费水平。

n_clusters=2时，聚类的结果

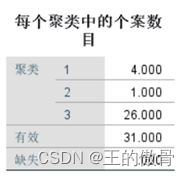
n_clusters=3时，聚类的结果

n_clusters=4时，聚类的结果

结论：从这几次聚类的比较中可以看出，消费水平相近的省市聚集在一类。而北京、上海和广东很稳定的一直聚集在同一类中，在当k = 4时，这样的一种聚类可以比较明显的看出消费层级。

K-Means的扩展改进

计算两条数据相似性时, Sklearn的K-Means默认使用的是欧式距离。虽然还有余弦相似度, 与马氏距离等多种方法，但没有设定计算距离方法的参数。如果要改变计算距离的公式时，可以改变K-means的源代码。

统计学中的聚类

1、分类和聚类的区别：

分类：是根据事物的本身的性质或特点去定义的。

聚类：是将物理或抽象对象的集合分成由类似的对象组成的多个类的过程

两者不同点在于聚类所要求的划分的标签是未知的。（即无监督学习）

聚类分析是一种探索性分析，在分类过程中，不必给出一个分类的标准，聚类分析能够从样本数据出发，自动进行分类。

2、聚类的原理：

1、当分类对象属性过多时，为了保证分类的合理性，我们要选择适当的分类指标，来描述对象间联系的紧密程度。

直观理解→按距离远近来划分

2、选多少个变量属性来进行聚类，就构成一个多少维度的空间，研究对象用空间中的点表示，一般规为，距离近的点为一类，距离远的点为另一类。

3、原则上同类间具有尽可能多的同性。

4、两类差距越大则分类效果越好。

K-Means算法

k均值聚类是最著名的划分聚类算法，由于简洁和效率使得他成为所有聚类算法中最广泛使用的。给定一个数据点集合和需要的聚类数目k，k由用户指定，k均值算法根据某个距离函数反复把数据分入k个聚类中。

K-means算法步骤：

K-means案例分析：

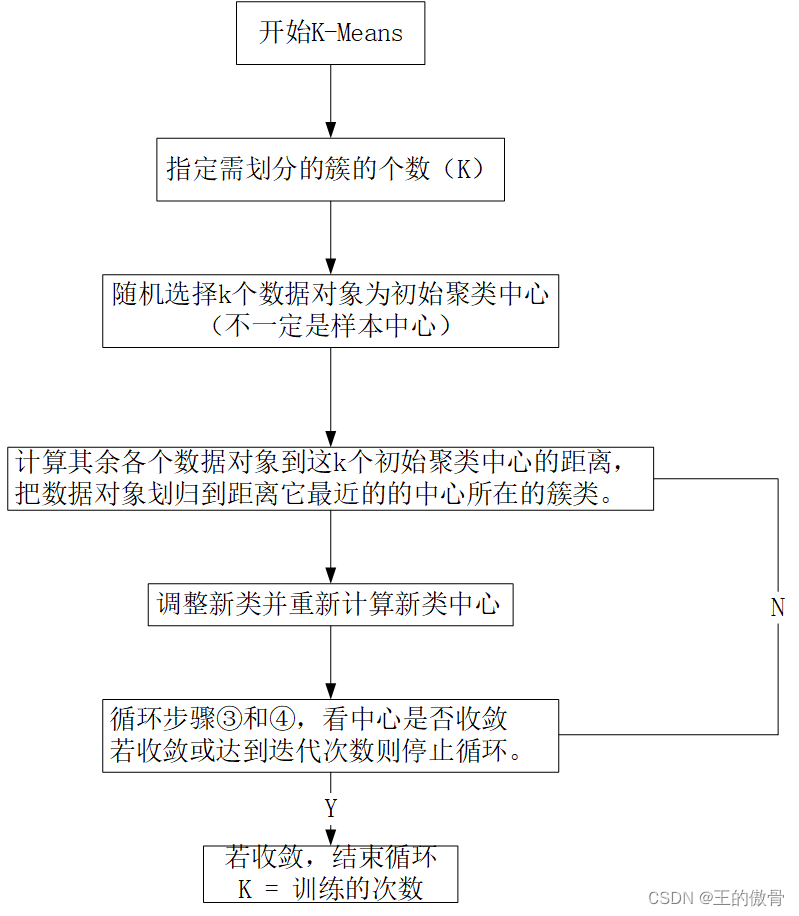
例4：对16个地区居民生活水平的进行分析。数据为我国16个地区的农民在1982年支出的抽样情况，每个地区都调查反映每个人平均生活消费支出情况的6个指标。利用K-Means聚类的方法分析进行分类。

Step1：第一步一定是先将数据预处理（查找缺失值、消除量纲与标准化）

在SPSS进行操作得到：

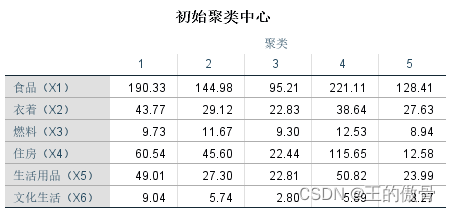
初始聚类中心表：系统自动选出了5个初始聚类中心，分别为以下地区：北京、江苏、河北、上海和内蒙古。以上初始类中心基本包括了16个地区中高消费到低消费地区的各个层次。

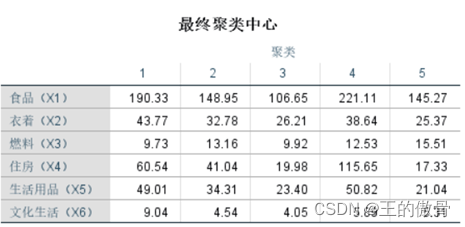
最终聚类中心：表示各类地区消费水平指数。(实际意义)

最终聚类中心的距离：表示各个类之间的差距。

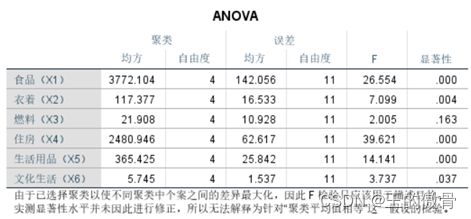
方差分析表：表示各指数在不同地区的均值比较，即五类地区之间的差异。观测图中的数据：X3和X6在聚类分析得出的类别都呈现出了显著差异，可见这两个变量在聚类分析中没有起到作用，当前聚类分析结果可以不能用数据的聚类。

2、K-means案例分析（2）：

例5：针对于对31个省份的情况用SPPSS聚类与机器学习的聚类作比较来了解1999年的国民平均收入情况。

Step1:由于此数据的量纲一致，所以先直接用K-Means聚类得到下图（17），分析表中信息当k = 3时，很明显的将北京、上海和广东聚到了一类（与机器学习数据一样）但身下的两类就有了明显差异。

Step2：将数据进行了标准化后，分析了当k=3的时候的聚类模型。

将北京、天津、上海和浙江聚到了一类。

结论：通过将数据处理后的模型的聚类效果好、精度高和可用性强。

2、聚类的目的：

1、聚类的目标是同一类对象的相似度尽可能大，不同类对象之间的相似度尽可能的小。

2、设计抽样方案（分层抽样）预分析过程（简化数据）细分市场、个体消费行为划分（先聚类，然后再利用判别分析进一步研究各个群体之间得差异）

系统聚类与K-means的区别

系统聚类	K-means聚类
事先不需要确定要分多少类自动确定最佳分类数	事先需要确定要分多少类
计算量较大，对大量数据的聚类效率不高	计算量小，适于数据量大的聚类
可对个案和变量聚类	不能对变量聚类，所使用的变量必须是连续变量。
可以绘制出树状聚类图，方便使用者直观选择类别

3、聚类分析需要注意的问题

1、对于一个实际问题要根据分类的目的来选取指标，指标选取的不同分类结果一般也不同。

2、样品间距离定义方式的不同，聚类结果一般也不同。

3、聚类方法的不同，聚类结果一般也不同（尤其是样品特别多的时候）。最好能通过各种方法找出其中的共性。

4、要注意指标的量纲，量纲差别太大会导致聚类结果不合理。

5、聚类分析的结果可能不令人满意，因为我们所做的是一个数学的处理，对于结果我们要找到一个合理的解释。

6、当要确定k的值时可以通过肘部法则（用图形估计聚类的数量）

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/一键难忘520/article/detail/812920

数学建模之聚类算法（K-means）_k平均聚类初始聚类中心和最终聚类中心是什么

K-means聚类算法

K-means的案例分析

K-Means的扩展改进

统计学中的聚类

1、分类和聚类的区别：

2、聚类的原理：

K-Means算法

K-means算法步骤：

K-means案例分析：

2、K-means案例分析（2）：

2、聚类的目的：

3、聚类分析需要注意的问题