遗传算法（Genetic Algorithm）

本文为阅读《遗传算法原理及应用》的笔记和心得
ISBN：7-118-02062-1

遗传算法简介

遗传算法是模拟生物在自然环境中的遗传和进化过程中而形成的一种自适应全局优化概率搜索算法
总的来说，求最优解解或近似最优解的方法主要有三种：枚举法、启发式算法和搜索算法。

• 枚举法：枚举出可行解集合内的所有可行解，以求出精确最优解。该方法的求解效率比较低。
• 启发式算法：寻求一种能产生可行解的启发式规则，以找到一个最优解或近似最优解。效率较高，无通用性。
• 搜索算法：寻求一种搜索算法，该算法在可行解结合的一个子集内进行搜索操作，以找到问题的最优解或近似最优解。能在近似解的质量和求解效率上达到一种较好的平衡。

遗传算法中，将 n 维决策变量$$\mathrm{X}=[{\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,\cdots ,{{\mathrm{x}}_{\mathrm{n}}]}^{\mathrm{T}}$$
用 n 个记号 X_i ( i=1, 2, 3, … , n)所组成的符号串X来表示：$$\mathrm{X}={\mathrm{X}}_1{\mathrm{X}}_2\cdot \cdot \cdot {\mathrm{X}}_{\mathrm{n}}\Rightarrow \mathrm{X}=[{\mathrm{x}}_1,{\mathrm{x}}_2,{\mathrm{x}}_3,\cdots ,{{\mathrm{x}}_{\mathrm{n}}]}^{\mathrm{T}}$$
把每一个$X_i$看作一个遗传基因，它的所有可能取值称为等位基因，这样，X就可看做由 n 个遗传基因所组成的一个染色体。

最简单的等位基因是由 0 和 1 这两个整数组成的，相应的染色体就可表示为一个二进制符号串。

染色体 X 也称为个体 X ，对于每一个个体 X ，需要按照一定规则确定出其适应度，个体的适应度与其对应的个体表现型 X 的目标函数相关联。
X 越接近于目标函数的最优点，其适应度越大；反之，其适应度越小。

生物的进化是以集团为主体的。与此相对应，遗传算法的运算对象是由 M 个个体所组成的集合，称为群体。

遗传算法的过程：
遗传算法的运算过程也是一个反复达代过程、第 t 代群体记做P ( t )，经过一代遗传和进化后，得到第 t+1 代群体，它们也是由多个个体组成的集合，记做 P (t +1)。这个群体不断地经过遗传和进化操作，并且每次都按照优胜劣汰的规则将适应度较高的个体更多地遗传到下一代，这样最终在群体中将会得到一个优良的个体 X，它所对应的表现型 X将达到或接近于问题的最优解 $X^{\ast }$

生物的进化过程主要是通过染色体之间的交叉和染色体的变异来完成的。
与此相对应，遗传算法中最优解的搜索过程也模仿生物的这个进化过程，使用所谓的遗传算子 ( genetic operators )作用于群体 P( t ) 中，进行下述遗传操作，从而得到新一代群体P ( t+1 )。

• 选择（selection）：根据各个个体的适应度，按照一定的规则或方法，从第 t 代群体 P( t )中选择出一些优良的个体遗传到下一代群体P ( t+1 )中。
• 交叉（crossover）：将群体 P ( t )内的各个个体随机搭配成对，对每一对个体，以某个概率（crossover rate）交换它们之间的部分染色体。
• 变异（mutation）：对群体P ( t )中的每一个个体，以某一概率（称为变异概率， mutation rate）改变某一个或某一些基因座上的基因值为其他的等位基因。

使用上述三种遗传算子（选择算子，交叉算子，变异算子）的遗传算法的主要运算过程如下所述：

1. 初始化。设置进化代数计数器 t <- 0;设置最大进化代数 T ; 随机生成 M 个个体作为初始群体P ( 0 )。
2. 个体评价。计算群体 P( t )中各个个体的适应度。
3. 选择运算。将选择算子作用于群体。
4. 交叉运算。将交叉算子作用于群体。
5. 变异运算。将变异算子作用于群体。群体 P ( t )经过选择、交叉、变异运算之后得到下一代群体 P (t + 1)。
6. 终止条件判断。若 i ≤ T，则: t <- t +1，转到步骤二; 若 t > T，则以进化过程中所得到的具有最大适应度的个体作为最优解输出，终止计算。

遗传算法的手工模拟计算示例

为了更好地理解遗传算法地运算过程，下面用手工计算来简单地模拟遗传算法地各个主要执行步骤。
{ m a x f ( x 1 , x 2 ) = x 1 2 + x 2 2 s . t . x 1 ∈ { 0 , 1 , 2 , ⋅ ⋅ ⋅ , 7 } x 2 ∈ { 0 , 1 , 2 , ⋅ ⋅ ⋅ , 7 } $$\begin{cases} max&{f}\left({x}_1, {x}_2 \right) ={ {x}_1}^2+{ {x}_2}^2\\ {s}.{t}.&{x}_1\in \left\{ 0, 1, 2,\cdot \cdot \cdot ,7 \right\}\\ &{x}_2\in \left\{ 0, 1, 2,\cdot \cdot \cdot ,7 \right\}&\\ \end{cases}$$ ⎩ ⎨ ⎧​maxs.t.​f(x1​,x2​)=x1​2+x2​2x1​∈{0,1,2,⋅⋅⋅,7}x2​∈{0,1,2,⋅⋅⋅,7}​​

现对其主要运算过程作如下解释：

1. 个体编码。

遗传算法地运算对象是表示个体的符号串，所以必须把变量 $x_1$，$x_2$ 取0 ~ 7之间的整数，可分别用 3 位无符号二进制整数来表示，将它们连接在一起所组成的 6 位无符号二进制整数就形成了个体的基因型，表示一个可行解。例如，基因型 X = 101110 所对应的表现型是：$X=[5,6{]}^T$ 。个体的表现型 x 和基因型 X 之间可通过编码和解码程序相互转换。

2. 初始群体的产生。

遗传算法是对群体进行的进化操作，需要给其准备一些表示起始搜索点的初始群体数据。本例中，群体规模的大小取为 4，即群体由 4 个个体组成，每个个体可通过随机方法产生。

3. 适应度计算。

遗传算法中以个体适应度的大小来判定各个个体的优劣程度，从而决定其遗传机会的大小。本例中，目标函数总取非负值，并且是以求函数最大值为优化目标，故可直接利用目标函数值作为个体的适应度。

4. 选择计算。

选择运算 (或称为复制运算)把当前群体中适应度较高的个体按某种规则或模型遗传到下一代群体中。一般要求适应度较高的个体将有更多的机会遗传到下一代群体中本例中，我们采用与适应度成正比的概率来确定各个个体复制到下一代群体中的数量。其具体操作过程是:先计算出群体中所有个体的适应度的总和 $\sum f_i$ ；其次计算出每个个体的适应度的大小 $f_i/\sum f_i$ ,表示每个个体被遗传到下一代群体中的概率，每个概率值组成一个区域（可理解为区间长度），全部概率值之和为 1 ；最后再产生一个 0 到 1 之间的随机数，依据该随机数出现在上述哪一个概率区域内来确定各个个体被选中的次数。

5. 交叉运算

交叉运算是遗传算法中产生新个体的主要操作过程，它以某一概率相互交换某两个个体之间的部分染色体。本例采用单点交叉的方法，其具体操作过程是：先对群体进行随机配对，其次随机设置交叉点位置，最后再相互交换配对染色体之间的部分基因。

6. 变异运算。

变异运算是对个体的某一个或某一些基座上的基因值按某一较小的概率进行改变，它也是产生新个体的一种操作方法。本例中，我们采用基本位变异的方法来进行变异运算，其具体操作过程是：首先确定出各个个体的基因变异位置；然后依照某一概率将变异点的原有基因值取反。

对群体 P( t ) 进行一轮选择、交叉、变异运算之后可得到新一轮的群体 P ( t+1 )。
经过多次迭代，便可以得到 111111 这一基因序列，解码后即[ 7 , 7 ]，max=98。

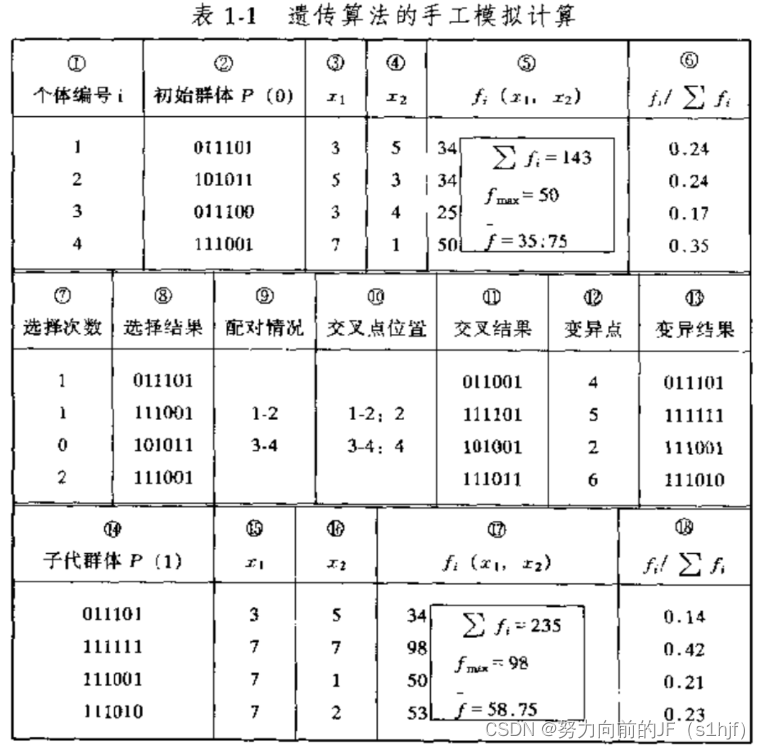
遗传算法的特点

1. 遗传算法以决策变量的编码作为运算对象。
   这种对决策变量的编码处理方式，使得我们再优化计算过程中可以借鉴生物学中染色体和基因等概念，可以模仿生物界中生物的遗传和进化等机理，也使得我们可以方便地应用遗传操作算子。
   特别是对一些无数值概念或很难有数值概念，而只有代码概念的优化问题，编码处理方式更显示出了其独特的优越性。

2. 遗传算法直接以目标函数值作为搜索信息。
   遗传算法仅使用由目标函数值变换来的适应度函数值，就可以确定进一步的搜索方向和搜索范围，无需目标函数的导数值等其他一些辅助信息。

3. 遗传算法同时使用多个搜索点的搜索信息。
   遗传算法从由很多个体所组成的一个初始群体开始最优解的搜索过程，而不是从一个单一的个体开始搜索。对这个群体所进行的选择、交叉、变异等运算，产生出的乃是新一代的群体，在这之中包括了很多群体信息。这些信息可以避免搜索一些不必搜索的点，所以实际上相当于搜索了更多的点，这是遗传算法所特有的一种隐含并行性。

4. 遗传算法使用概率搜索技术。
   遗传算法属于一种自适应概率搜索技术，其选择、交叉、变异等运算都是以一种概率的方式进行的，从而增加了其搜索过程的灵活性。

遗传算法的应用

1. 函数优化
2. 组合优化
3. 生产调度问题
4. 自动控制
5. 图像处理
6. 遗传编程
7. 机器学习

遗传算法的基本实现技术

编码方法

在遗传算法的运行过程中，它不对所求解问题的实际决策变量直接进行操作，而是对表示可行解的个体编码施加选择、交叉、变异等遗传运算，通过这种遗传操作来达到优化的目的。

在遗传算法中如何描述问题的可行解，即把一个问题的可行解从其解空间转换到遗传算法所能处理的搜索空间的转换方法就称为编码。

编码是应用遗传算法时要解决的首要问题，也是设计遗传算法时的一个关键步骤。

• 二进制编码方法
• 格雷码编码方法
• 浮点数编码方法（真值编码方法）
• 符号编码方法
• 多参数级联编码方法
• 多参数交叉编码方法