Java数据结构——二叉搜索树_根节点的值

14天阅读挑战赛

 文章目录

1.概念

2.操作—查找

3.操作—插入

4.操作—删除

---

1.概念

二叉搜索树又称二叉排序树，或者是一棵空树，或具有以下性质:

若该树左子树不为空，则左子树上所有节点的值小于根节点的值

若该树右子树不为空，则右子树上所有节点的值大于根结点的值

二叉搜索树的左右子树也是二叉搜索树

 如图：

int[] arr1 = {10,6,16,3,9,14,19} 

int[] arr2 = {10,6,3,9}                                                

2.操作—查找

 查找value步骤：

如果根节点不为空

看根节点的值是否等于value,等于返回true

根节点的值>value，继续在根节点左子树查找

根节点的值<value，继续在根节点右子树查找

代码

public TreeNode serach(int val){
        TreeNode cur = root;
        while(cur != null){
            if(cur.val > val){
                cur = cur.left;
            } else if (cur.val < val) {
                cur = cur.right;
            }
            else{
                return cur;
            }
        }
        return null;
    }

当时满二叉树时，查找效率最高，平均比较次数为log(2(N))

如果是但分支，则是O(N)

3.操作—插入

如果要插入的节点为空，根 == null，直接插入，返回true

定义一个prev和cur，从root开始查找，当cur为空时，找到要插入的位置，即prev的下一个节点

代码

public boolean insert(int key){
        if(root == null){
            TreeNode root = new TreeNode(key);
            return true;
        }
        TreeNode parent = null;
        TreeNode cur = root;
        while(cur != null){
            if(cur.val > key){
                parent = cur;
                cur = cur.left;
            } else if (cur.val < key) {
                parent = cur;
                cur = cur.right;
            }
            else{
                return false;
            }
        }
        TreeNode node = new TreeNode(key);
        if(parent.val < key){
            parent.right = node;
        }
        else{
            parent.left = node;
        }
        return true;
    }

测试

int[] array = {10,6,16,3,9,14,19,13};
        for (int i = 0; i < array.length; i++) {
            binarySerachTree.insert(array[i]);
        }

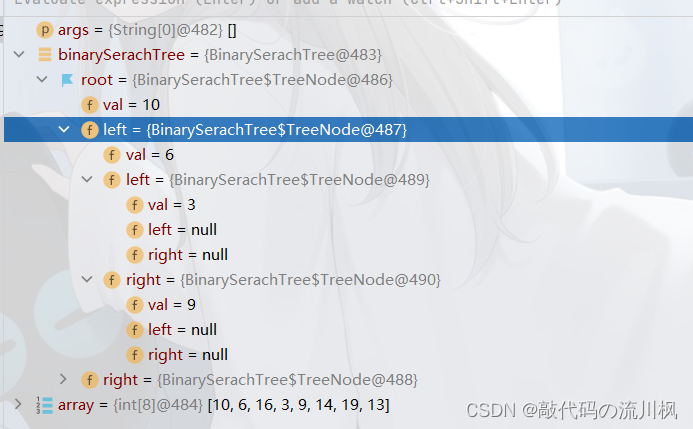
成功插入

binarySerachTree.inorder(binarySerachTree.root);

中序遍历

4.操作—删除

删除分为三种情况

第一种情况，cur.left == null 又分为三种情况。cur是要删除的节点

 第二种情况，cur.right == null 又分为三种情况

 

 

 第三种情况，cur左右都不为空的情况

我们使用后续节点一个恰当的节点的值替换掉要删除的节点的值，然后删除掉被替换的节点

我们可以发现，要删除16，能替换的节点有值为15和值为18这两个节点，我们用值为18这个节点替换，替换后删除这个节点

当target.left不为空时，一直向左寻找，找到最小值，和cur.val交换

然后删除target这个节点，让targetParent = target.right即可，没有就是空

 到这里还有个情况没有考虑

cur的右子树的左数为空时，19这个节点就用来替换

代码

public void removeNode(TreeNode parent,TreeNode cur){
        if(cur.left == null){
            //cur左边为空分为三种情况
            if(cur == root){
                root = cur.right;
            }
            if(cur == parent.left){
                parent.left = cur.right;
            }
            if(cur == parent.right){
                parent.right = cur.right;
            }
        }
        //右边为空的三种情况
        else if (cur.right == null) {
            if(cur == root){
                root = cur.left;
            }
            if(cur == parent.left){
                parent.left = cur.left;
            }
            if(cur == parent.right){
                parent.right = cur.left;
            }
        }
        //cur的左右都不为空的情况
        else{
            TreeNode target = cur.right;
            TreeNode targetParent = cur;
            while(target.left != null){
                targetParent = target;
                target = target.left;
            }
            //交换
            cur.val = target.val;
            if(target == targetParent.left) {
                targetParent.left = target.right;
            }
            else {
                targetParent.right = target.right;
            }
        }