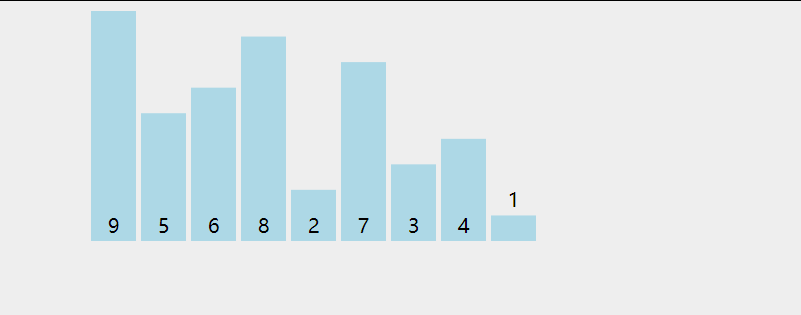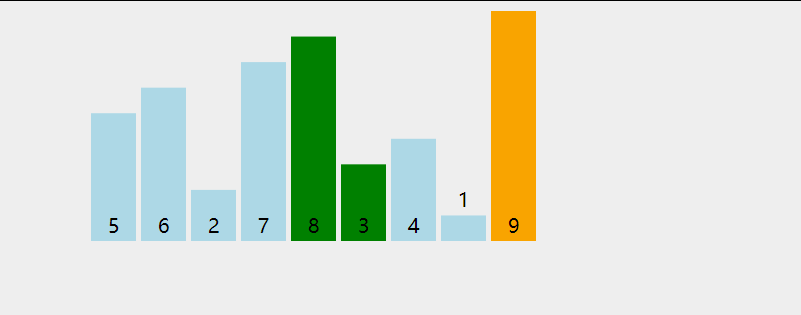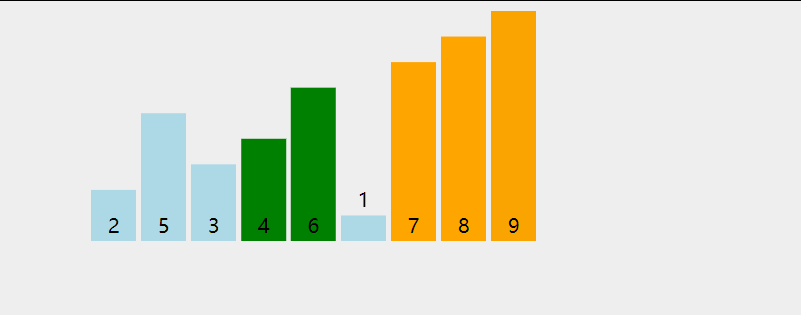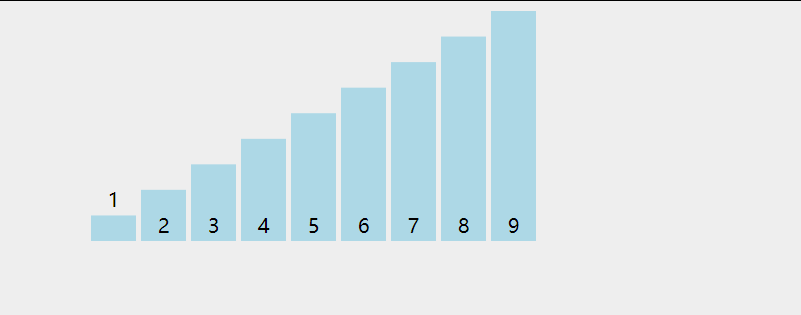- 1python爬取网页内容大作业,python爬取网页内容代码_python网络爬虫大作业
- 2利用awstats分析apache日志
- 3github 续传和加速_ghproxy
- 4Flink,spark对比
- 5鸿蒙Harmony--文本组件Text属性详解
- 6Mysql使用 SHOW TABLE STATUS命令显示表的相关信息_show table status 写到表里
- 708 - 程序的输入和输出_程序的输出
- 8OpenCv之简单的人脸识别项目(动态处理页面)_opencv人脸识别项目
- 9渗透测试工具库总结(全网最全)_mip22 is a advanced phishing tool
- 10Xilinx FPGA Multiboot-使用ICAPE2原语_icape2原语使用
【数据结构】八大排序算法详细实现--强烈推荐_selecting排序
赞
踩
前言
我们都知道,排序算法是编程高级语言里面极其重要的算法,虽然在C语言中,我们排序可以直接使用库函数qsort()函数,在C++中,我们可以使用sort()等函数直接完成对数据的排序。
但是,在这经典的八大排序算法中,有很多经典而且重要的思想,是需要我们掌握的,我们在刷题的时候,会用到这些排序思想,是我们编程解题离不开的。
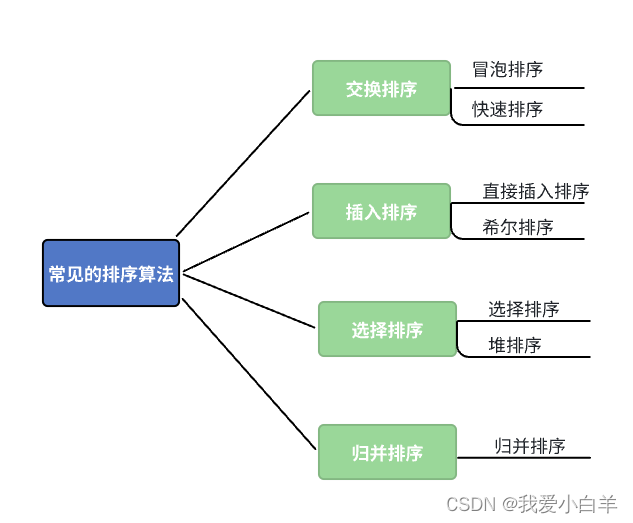
因此:接下来,随着博主的步伐和顺序,一起学习这经典的八大排序
排序的概念
排序:所谓排序,就是使一串记录,按照其中的某个或某些关键字的大小,递增或递减的排列起来的操作。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
内部排序:数据元素全部放在内存中的排序。
外部排序:数据元素太多不能同时放在内存中,放在磁盘里面的排序。
冒泡排序 bubbleSort
冒泡排序顾名思义,就是数据向冒泡一样浮到序列的最后。具体过程为:每轮排序中相邻的两个数进行比较,较大的数置于右边,然后继续进行下一相邻数字的比较,一轮排序过后,最大的数字就会置于最右边。然后进行第二轮排序,第三轮…直到不再有相邻的数字可以比较。
通过一个动画,我们就可以很好地理解这个过程
很明显,这个代码需要用两层循环来实现,第一层用来控制循环的轮数,里层用来控制每一轮相邻数字的交换。
冒泡排序的优化:
对于冒泡排序,我们可以做出一些优化:当我们发现有一轮排序没有任何相邻数进行交换的时候,说明,序列已经有序了,不需要再进行下一轮的排序了,因此,我们可以增加一个变量Change,来记录一轮里是否有数字进行了交换。
void bubble_sort(int* arr, int sz) { for (int i = 0; i < sz - 1; i++) {//外层循环 //tips:只需要sz-1次,因为最后一次是没有两个数可以交换了 int Change= 0; for (int j = 0; j < sz - 1 - i; j++) {//这里的sz-1-i,我们只要画一画,把例子写出来就可以很好地明白,这里不赘述了 if (arr[j] > arr[j + 1]) { swap(arr[j],arr[j+1]);//交换两者的值,注:C语言实现swap需要传地址。 Change= 1; } } //每一轮走完之后,如果Change==0;直接return if (Change==0) return; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
冒泡排序的特性总结:
冒泡排序是一个非常容易理解的排序。
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(n^2) | O(N) | O(N^2) | O(1) | 稳定 |
快速排序 quickSort
快速排序是Hoare于1962年提出的一种二叉树结构的交换排序方法,其基本思想为:任取待排序元素序列中
的某元素作为基准值,按照该排序码将待排序集合分割成两子序列,左子序列中所有元素均小于基准值,右
子序列中所有元素均大于基准值,然后最左右子序列重复该过程,直到所有元素都排列在相应位置上为止快速排序:
1.先从数列中选取一个元素作为基准数 (key)
2. 扫描数列,将比基准数小的元素全部放到它的左边,大于或等于基准数的元素全部放到它的右边,得到左右两个区间
3. 再对左右区间重复第二步,直到各区间元素个数少于两个。 这是一个挖坑填数+分治的思想
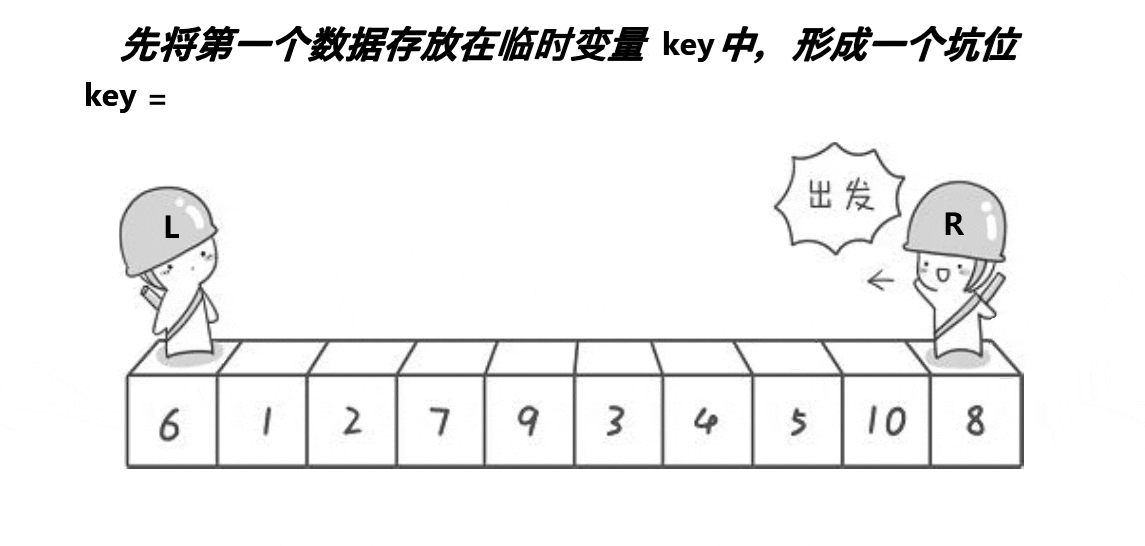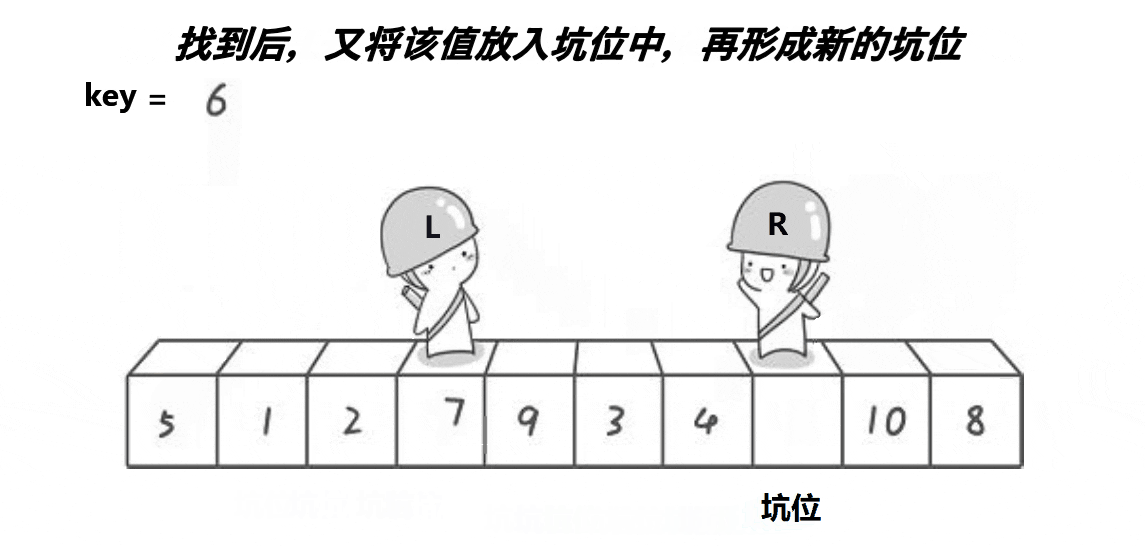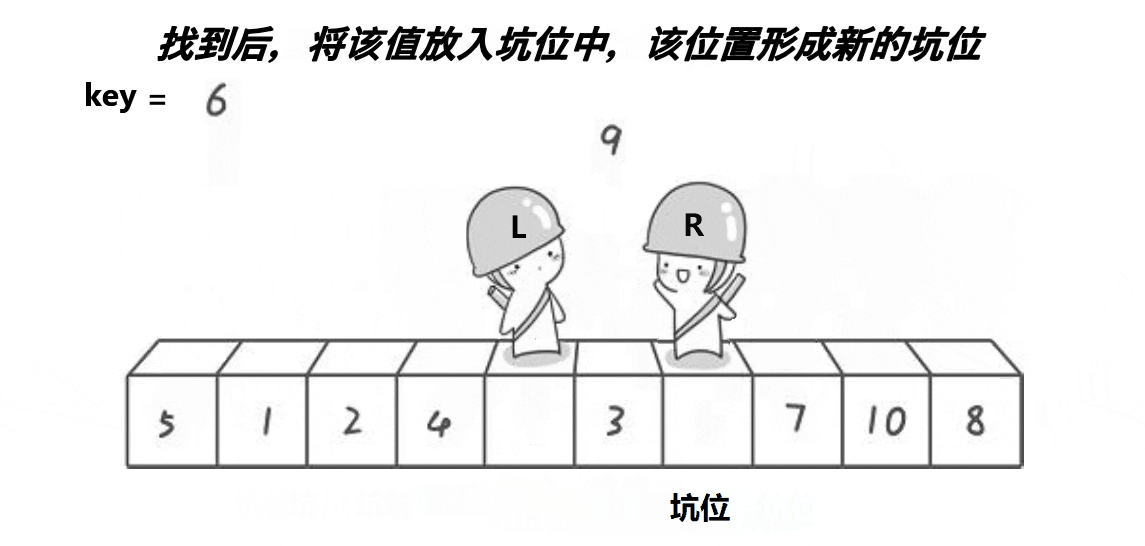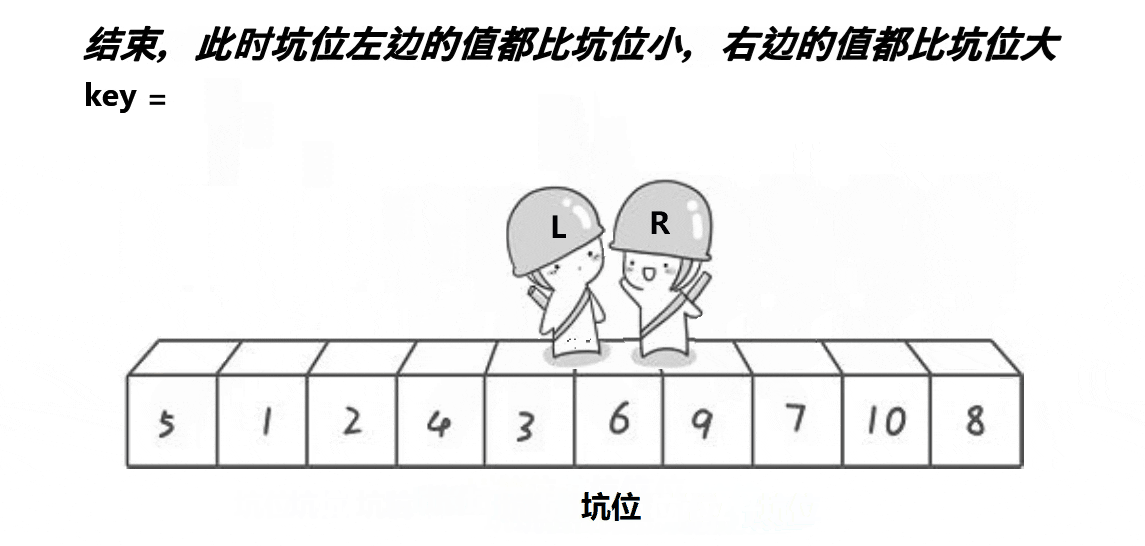
代码实现:
递归实现:
void quickSort(int* arr, int begin,int end) { //区间不存在,或者只有一个值则不需要再处理 if (begin>=end){ return; int left= begin,right=end; int keyi = left;//首先选取最左边的数为中心轴 while (left < right) { //右边先走,找小 while(left<right&& arr[right]>=arr[keyi]) { --right; } //左边再走,找大 while(left<right&&arr[left]<=arr[keyi]) { ++left; } Swap(&arr[left],&arr[right]); } Swap(&arr[keyi],&arr[left]); keyi=left; //[begin,keyi-1]keyi[keyi+1,end] quickSort(arr, begin,keyi-1);//基准值左边序列快排 quickSort(arr,keyi+ 1,end);//基准值右边序列快排 } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
非递归代码实现
- 用数据结构栈模拟递归过程
void QuickSortNonR(int* a, int begin, int end) { ST st; StackInit(&st); StackPush(&st, end); StackPush(&st, begin); while (!StackEmpty(&st)) { int left = StackTop(&st); StackPop(&st); int right = StackTop(&st); StackPop(&st); int keyi = PartSort3(a, left, right); // [left, keyi-1] keyi[keyi+1, right] if (keyi + 1 < right) { StackPush(&st, right); StackPush(&st,keyi + 1); } if (left < keyi - 1) { StackPush(&st, keyi - 1); StackPush(&st, left); } } StackDestroy(&st); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
快速排序的优化:
在我们介绍的代码中,最初选取的基准轴是来自**最左边的数,**这样会导致区间是很不均匀的。我们采取分治的思想,区间均匀的话,可以减少递归深度。
所以我们在此基础上是可以适当进行优化的:
- 采用更合理的基准数(中心轴),减少递归的深度。从数列中选取多个数,取中间数。
- 结合插入排序,区间在10个元素之内采用插入排序,效率更高。

在这里博主不再多做讲解了,最重要的就是理解我们最基本的那个快速排序的分治思想,后续优化的话,会单独写一篇博文,见链接:链接: 快速排序的优化写法-基准值选取优化及深度剖析
快速排序的特性总结:
快速排序整体的综合性能和使用场景都是比较好的,所以才敢叫快速排序
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(N*logN) | O(N) | O(N*logN) | O(logN) | 不稳定 |
插入排序 insertSort
**
插入排序的基本思想是把待排序的数据按其值的大小逐个插入到一个已经排好序的有序序列中,直到所有的数据插入完为止,得到一个新的有序序列 。
在其实现过程使用双层循环,外层循环对除了第一个元素之外的所有元素,内层循环对当前元素前面的有序表进行待插入位置查找,并进行移动
一般,插入排序对于序列元素较少的情况,比较高效。
**
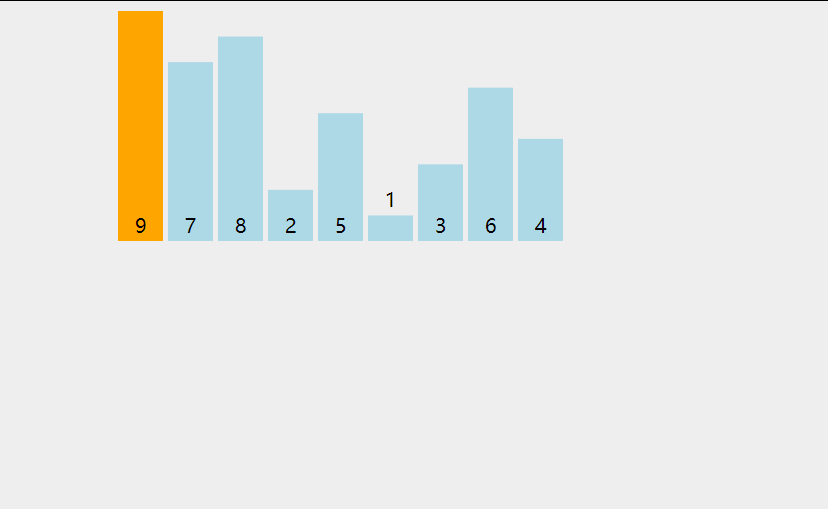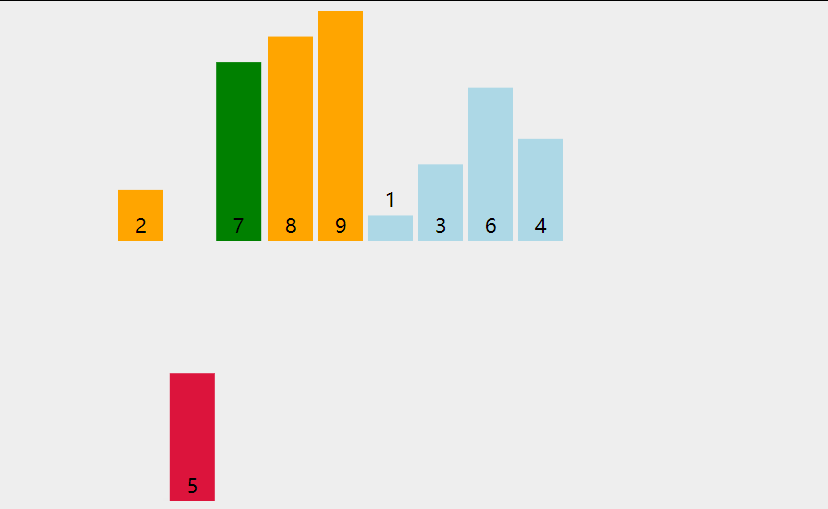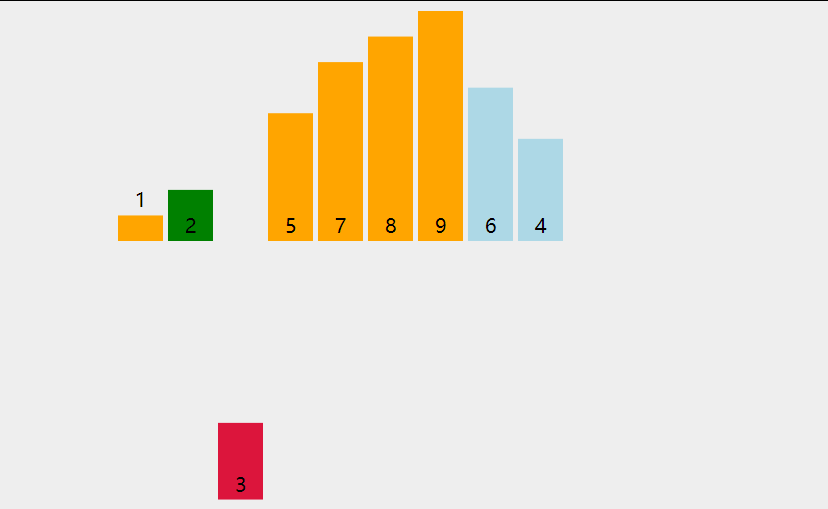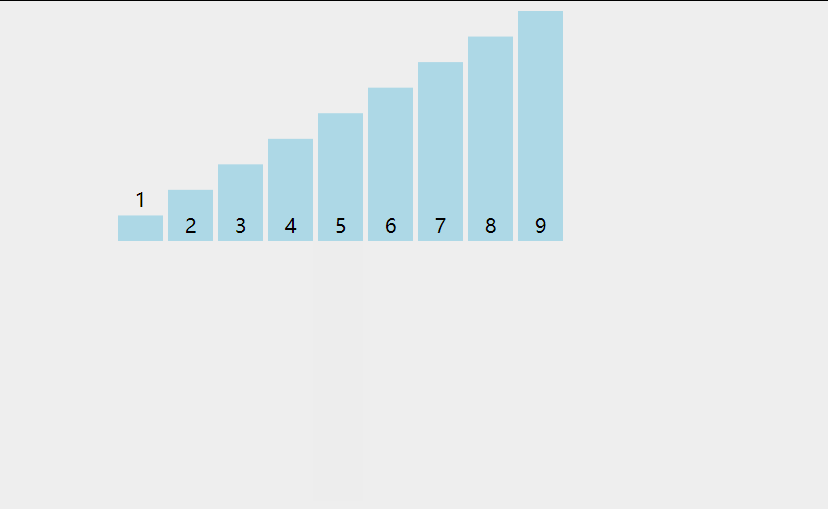
tips:挪动数据的时候,循环一定是反向的,从前往后挪,就要从后往前循环,否则数据会被前一个数覆盖的。
代码实现:
void insertSort(int* arr, int sz) { int sortNum = 0; for (int i = 1; i < sz; i++) { sortNum = arr[i];//要排序的数字 for (int j = i - 1; j >= 0; j--) {//因为要从待排序那个数的前一个数开始,往后挪一个 //从后往前挪动,所以用反向循环 //先判断,因为只需要挪动比待排序数字大的数字 if (arr[j] < sortNum) { break; } arr[j + 1] = arr[j];//一个个挪动数据 } arr[j + 1] = sortNum; //所以此时的j指向空位置前一个位置,所以arr[j+1]=sort; } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
直接插入排序的不足和优化:
1.寻找插入位置
2.移动元素
优化方案:
1.对已经排好序的序列,采用二分查找的方法
2.使用希尔排序
直接插入排序的特性总结:
元素集合越接近有序,直接插入排序算法的时间效率越高.
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(N^2) | O(N) | O(N^2) | O(1) | 稳定 |
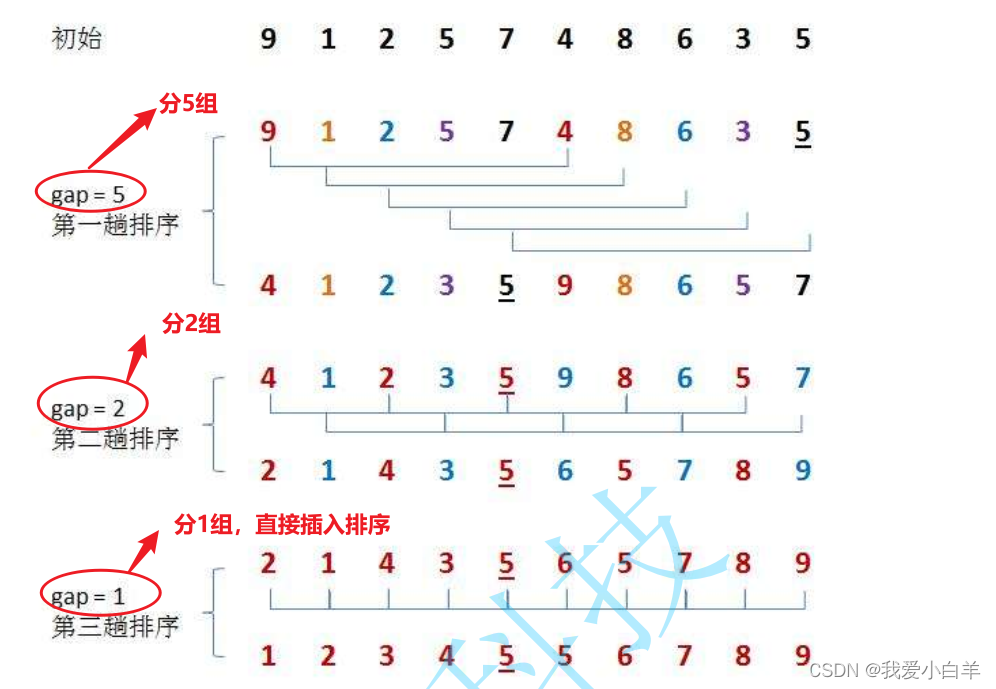
希尔排序ShellSort:
希尔排序又称缩小增量排序。希尔排序法的基本思想是:先选定一个整数K,把待排序文件中所有数据分成多个组,所有距离为K的数据分在同一组内,并对每一组内的数据进行排序。然后,取,重复上述分组和排序的工作。当到达K=1时,所有数据在统一组内排好序。
大致思想是:先让数列整体大致有序,然后多次调整分组方式,使数列更加有序,最后再使用一次插入排序。
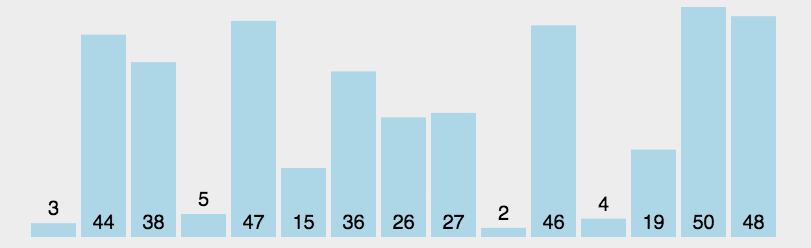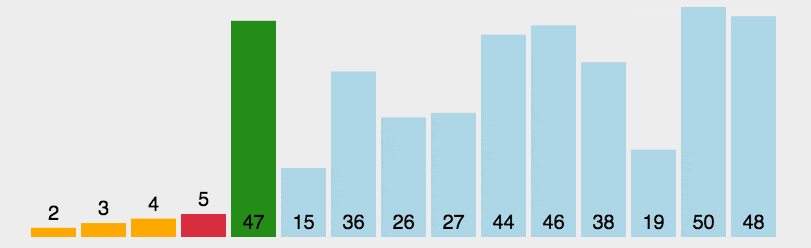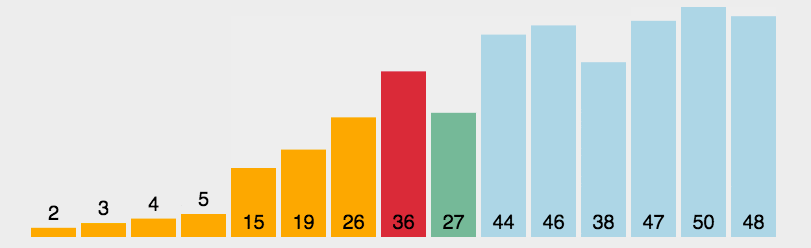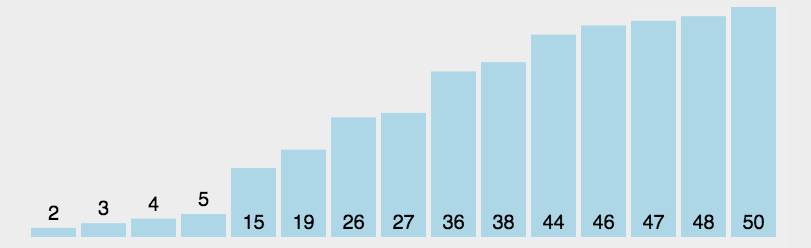
看到这些,我们肯定不明白,动画也不好表示希尔排序的过程,因此,用一张图来试着理解希尔排序的过程。
在希尔排序当中,引入了step,即步长,表示分组系数
思考:
为什么要在最后一次插入排序之前这么麻烦整这么多次,这样高效吗?
其实,这正是希尔排序的精妙所在,试想,如果我们有个很小的数字,以上面那组数为例,加入那个2,在很靠后的位置的时候。按照插入排序的原理,我们需要从后往前找,找2应该插入的位置,而2应该是最前面的,因此,我们就要将很多个数据分别向后挪动一个位置,这样是非常低效的。而我们在经过前面一些操作之后,序列已经大致有序了,因此,肯定不存在挪动很多个数据的一个情况。
因此,希尔排序的核心思想就是:1)在做插排的时候,查找次数减少,2)插排的时候移动元素次数减少。
关于希尔增量的讨论:
一般的话,**步长是二分得到的,**那为什么要这样二分呢,有其他分组方式吗?
希尔排序也叫缩小增量排序,
关于希尔增量的选取,是一个数学难题,没有准确的说法。
代码实现:
void ShellSort(int* arr, int sz) { int gap= sz; while(gap>1) { gap=gap/3+1; //gap=gap/2;使用二分法 for (int i= 0 ; i<sz-gap; i++) { %%这个地方代表不同的分组 int end=i; int tmp=arr[end+gap]; while(end>=0) %%往前找到0 { if(tmp<a[end]) { a[end+gap]=a[end]; end-=gap; } else { break; } } a[end+gap]=tmp; } } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
希尔排序特性总结:
- 希尔排序是对直接插入排序的优化。
- 当gap > 1时都是预排序,目的是让数组更接近于有序。当gap == 1时,数组已经接近有序的了,这样就
会很快。这样整体而言,可以达到优化的效果。我们实现后可以进行性能测试的对比。 - 希尔排序的时间复杂度不好计算,因为gap的取值方法很多,导致很难去计算,因此在好些树中给出的
希尔排序的时间复杂度都不固定:

| 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|
| O(N^1.25) | O(1) | 不稳定 |
选择排序 selectingSort
基本思想:
每一次从待排序的数据元素中选出最小(或最大)的一个元素,存放在序列的起始位置,直到全部待排序的 数据元素排完 .
直接选择排序具体过程为:
第一次从待排序的数据元素中选出最小的一个元素,存放在序列的起始位置,然后再从剩余的未排序元素中寻找到最小(大)元素,然后放到已排序的序列的末尾。以此类推,直到全部待排序的数据元素的个数为零。
代码实现:
void selectSort(int* arr, int sz) {
int i = 0;
int j = 0;
for (int i = 0; i < sz - 1; i++) {
int min = i;%%默认最小的为左边
for (int j = i + 1; j < sz; j++) {
if (arr[j] < arr[min]) {
min = j;//打擂台
}
}
//出了这层循环之后,交换min和i的值,把i后面最小的放到i的位置
swap(arr[i], arr[min]);//交换二者的值
}
}
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
直接选择排序特性总结:
直接选择排序思考非常好理解,但是效率不是很好。实际中很少使用
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(N^2) | O(N^2) | O(N^2) | O(1) | 不稳定 |
堆排序 heapSort
堆排序(Heapsort)是指利用(堆)这种数据结构所设计的一种排序算法,它是选择排序的一种。它是
通过堆来进行选择数据。需要注意的是排升序要建大堆,排降序建小堆 堆:
堆一类特殊的数据结构的统称。堆通常是一个可以被看做一棵树的数组对象。堆总是满足下列性质:
- 堆中某个结点的值总是不大于或不小于其父结点的值;
- 堆总是一棵完全二叉树
堆排序的思路:
- 将无序的数组的各个数字看作一棵完全二叉树,而每个元素的下标所对应的节点如上面那张图所示,从下标0开始从上到下,从左到右。
- 将数组构建成大堆(或小堆),具体实现看代码。
- 将堆的最后一个元素和第一个元素(顶元素)交换,并将最后一个元素脱离出堆。
我们知道,步骤2将数组构建成大顶堆之后,顶元素就是最大的元素,我们在这一步就可以找到最大的元素了。然后我们取出这个元素,重复上面的步骤,就可以找到第二大的元素,第三大的…,最后就完成了排序
代码实现:
//向下调整算法 void _AdjustDown(HPDataType* a, int size, int parent) { int child = parent * 2 + 1; while (child < size) { //选出小的那个孩子节点 if (child + 1 < size && a[child + 1] < a[child]) { ++child; } if (a[child] < a[parent]) { //向下调整 swap(a[child], a[parent]); parent = child; child = parent * 2 + 1; } else { //无需调整 break; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
//升序--建大堆 //降序--建小堆 void heapSort(int* arr, int n) { //1.构建二叉树,构建大堆 //建堆方式1:O(N*logN) //for (i = 1; i < n; i++) //{ // AdjustUp(arr,i); //} //建堆方式2:O(N) for (int i = (n -1-1)/2; i >= 0; --i) { AdjustDown(arr,n,i); } //O(N*logN) int end=n-1; while(end>0) { swap(&arr[0],&arr[end]); AdjustDown(arr,end,0); --end; } };
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
堆排序特性总结:
- 堆排序使用堆来选数,效率搞了很多。
- 由以上推论过程可得建堆的时间复杂度为O(N);
向下调整算法的时间复杂度为O(log2N);
所以堆排序的时间复杂度为O(N*log2N);
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(n*logn) | O(n*logn) | O(n*logn)) | O(1) | 不稳定 |
归并排序 mergeSort
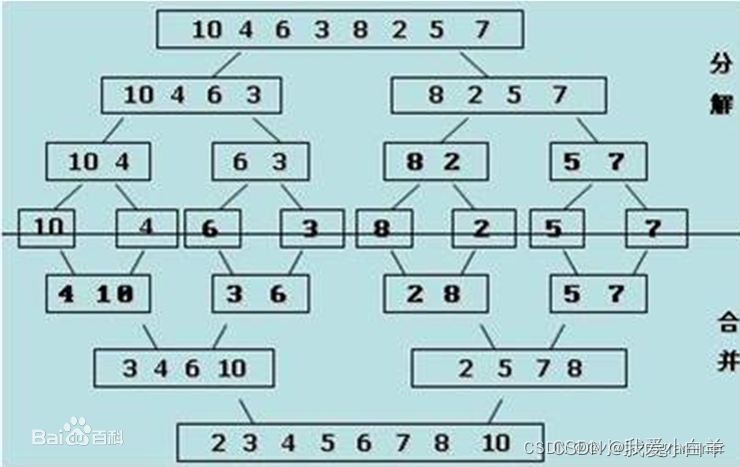
基本思想: 是建立在归并操作上的一种有效的排序算法,该算法是采用分治法(Divide and Conquer)的一个非常典型的应用。
- 将已有序的子序列合并,得到完全有序的序列;即先使每个子序列有序,再使子序列段间有序。若将两个有序表合并成一个有序表,称为二路归并
代码实现:
归并排序的实现方法由递归和循环两种方法。
递归方法的源代码简单一些
循环方法的源代码复杂一些,但效率高
递归的写法:
void _MergeSort(int *a, int begin, int end, int *tmp) { if (begin >= end) return; int mid = (begin + end) / 2; //找到排序中间的位置 // // [begin, mid] [mid+1, end] 分治递归,让子区间有序 %递归排序 _MergeSort(a, begin, mid, tmp); _MergeSort(a, mid + 1, end, tmp); // 归并的写法 int begin1 = begin, end1 = mid; int begin2 = mid + 1, end2 = end; int i = begin1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[i++] = a[begin1++]; } else { tmp[i++] = a[begin2++]; } } while (begin1 <= end1) { tmp[i++] = a[begin1++]; } while (begin2 <= end2) { tmp[i++] = a[begin2++]; } // 把归并数据拷贝回原数组 memcpy(a + begin, tmp + begin, (end - begin + 1) * sizeof(int)); } void MergeSort(int *a, int n) { %%开辟空间,归并排序会有空间的开销 int *tmp = (int *)malloc(sizeof(int) * n); if (tmp == NULL) { printf("malloc fail\n"); exit(-1); } _MergeSort(a, 0, n - 1, tmp); free(tmp); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
非递归写法:
void MergeSortNonR(int* a, int n) { //开辟空间 int* tmp = (int*)malloc(sizeof(int)*n); if (tmp == NULL) { printf("malloc fail\n"); exit(-1); } int gap = 1; while (gap < n) { for (int i = 0; i < n; i += 2 * gap) { // [i,i+gap-1][i+gap, i+2*gap-1] int begin1 = i, end1 = i + gap - 1; int begin2 = i + gap, end2 = i + 2 * gap - 1; // end1越界或者begin2越界,则可以不归并了 if (end1 >= n || begin2 >= n) { break; } else if (end2 >= n) { end2 = n - 1; } int m = end2 - begin1 + 1; int j = begin1; while (begin1 <= end1 && begin2 <= end2) { if (a[begin1] < a[begin2]) { tmp[j++] = a[begin1++]; } else { tmp[j++] = a[begin2++]; } } while (begin1 <= end1) { tmp[j++] = a[begin1++]; } while (begin2 <= end2) { tmp[j++] = a[begin2++]; } memcpy(a + i, tmp + i, sizeof(int)* m); } gap *= 2; } free(tmp); }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
- 34
- 35
- 36
- 37
- 38
- 39
- 40
- 41
- 42
- 43
- 44
- 45
- 46
- 47
- 48
- 49
- 50
- 51
- 52
- 53
- 54
- 55
- 56
- 57
- 58
- 59
- 60
归并排序特性总结:
- 归并的缺点在于需要O(N)的空间复杂度,归并排序的思考更多的是解决在磁盘中的外排序问题
| 最坏时间复杂度 | 最好时间复杂度 | 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|---|---|
| O(n*logn) | O(n*logn) | O(n*logn)) | O(N) | 稳定 |
非比较排序
- 非比较排序主要有 基数排序(校招不考)和 计数排序
- 非比较排序,适用于整数,非常小众
本篇博文,仅介绍计数排序
计数排序
基本思想:计数排序,是对哈希直接定址法的变形应用。 操作步骤:
- 统计相同元素出现次数
- 根据统计的结果将序列回收到原来的序列中
代码实现:
void CountSort(int *arr,int n) { int min=arr[0],max=arr[0]; for( int i=1;i<n;++i) { if(arr[i]<min) { min=arr[i]; } if(arr[i]>max) { max=arr[i]; } } //统计次数的数组 int range=max-min+1; int* countarray=(int*)malloc(sizeof(int)*range); //统计次数 for(int i=0;i<n;++i) { countarray[arr[i]-min]++; } //回写,排序 int j=0; for(int i=0;i<range;++i) { while(countarray[i]--) { arr[j++]=i+min; } } }
- 1
- 2
- 3
- 4
- 5
- 6
- 7
- 8
- 9
- 10
- 11
- 12
- 13
- 14
- 15
- 16
- 17
- 18
- 19
- 20
- 21
- 22
- 23
- 24
- 25
- 26
- 27
- 28
- 29
- 30
- 31
- 32
- 33
计数排序特性总结:
- 计数排序在数据范围集中时,效率很高,但是适用范围及场景有限。
| 时间复杂度 | 空间复杂度 | 稳定性 |
|---|---|---|
| O(MAX(N,range)) | O(range) | 稳定 |
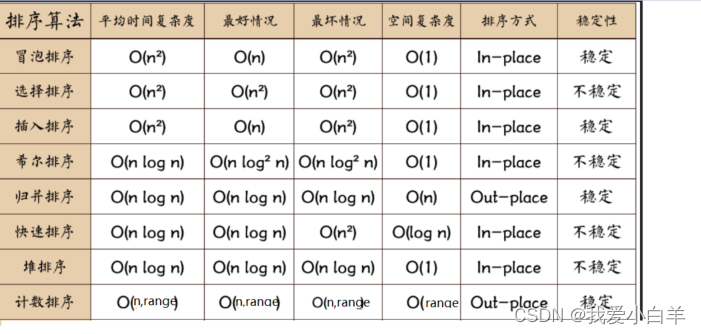
- 几种排序的时间复杂度和空间复杂度对比
尾声
看到这里,相信大家对堆这个数据结构有了了解了。
如果你感觉这篇博客对你有帮助,不要忘了一键三连哦