- 1微信小程序获取当前位置_taro vue 微信小程序 webview 里 获取当前定位
- 2精心整理800本PDF计算机编程类书籍,可以在线阅读,也可以下载,手快有,手慢无_计算机pdf图书
- 3MAC安装git的三种方式_mac 安装git
- 4计算机视觉(Computer Vision, CV)
- 5【Docker】win11安装docker不能启动,wsl 2 installation is incomplete报错_为什么安装了wsl 还是报错decker
- 6机器学习中的因果推理机制 (0) -- 引言_pearl casuality
- 7如何学习Java:糙快猛的大数据之路(主题知识地图)
- 8git生成change-id的解决方法
- 9转行软测&跳槽到新公司,工作怎样快速上手?_测试人员如何快速接手工作
- 10【工具使用】Dependency Walker使用_dependency walker下载
【pytorch损失函数(4)】nn.MSELoss,(Mean Squared Error,MSE) 均方误差(MSE)(squared L2 norm,平方L2范数)。它也被称为L2 Loss。
赞
踩
MSE 损失函数
1、是什么?
均方误差(MSE)是最常用的回归损失函数,它是目标变量和预测值的差值平方和。该函数给出输入x和目标y中的每个元素之间的均方误差(squared L2 norm,平方L2范数)。它也被称为L2 Loss。

2、数学表述
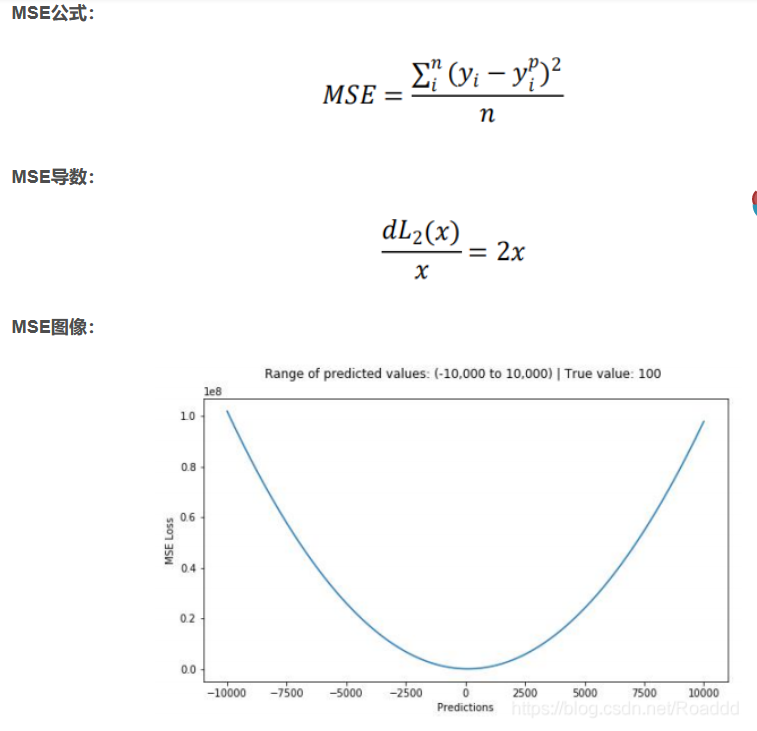
上图为均方误差函数图,其中目标真值为 100,预测范围在-10000 到 10000 之间,均方 误差损失(Y 轴)在预测值(X 轴)=100 处有最小值,范围为 0~∞。
主要问题:
导数变化,不稳定,尤其是在早期阶段(损失越大,导数越大),随着导数越来越小, 训练速度变得越来越慢。
3、MSE 梯度消失问题
二次函数 L = ( y − y ^ ) 2 2 L=\frac{(y-\hat{y})^2}{2} L=2(y−y^)2
采用链式法则求导,则有:
∂
L
∂
w
=
(
y
^
−
y
)
σ
(
z
)
′
x
\frac{\partial L}{\partial w}=(\hat{y}-y){\sigma(z)}'x
∂w∂L=(y^−y)σ(z)′x
∂
L
∂
b
=
(
y
^
−
y
)
σ
(
z
)
′
\frac{\partial L}{\partial b}=(\hat{y}-y){\sigma(z)}'
∂b∂L=(y^−y)σ(z)′
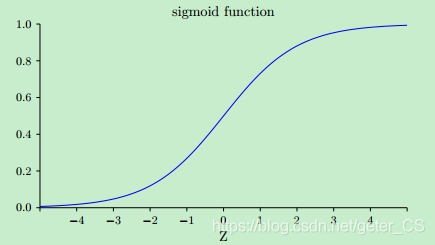
可以看出梯度都与sigmoid函数的梯度有关,如下图所示,sigmoid函数在两端的梯度均接近0,这导致反向传播的梯度也很小,这就这就不利于网络训练,这就是梯度消失问题 。
4、用途
5、L1 vs. L2 for Computer Vision
https://atcold.github.io/pytorch-Deep-Learning/en/week11/11-1/
In making predictions when we have a lot of different y’s:
- If we use MSE (L2 Loss), it results in an average of all y, which in CV it means we will have a blurry image.
- If we use L1 loss, the value y that minimize the L1 distance is the medium, which is not blurry, but note that medium is difficult to define in multiple dimensions.
Using L1 results in sharper image for prediction.
参考
https://atcold.github.io/pytorch-Deep-Learning/en/week11/11-1/


