热门标签
热门文章
- 12024年网络安全最新k8s学习-k8s资源对象与yaml结构_容器服务yaml配置 status(2)，2024年最新网络安全开发学习视频
- 2ChatGLM-6B的部署步骤_A1_chatglm3-6b 硬件要求
- 3C#进阶-ASP.NET WebForms调用ASMX的WebService接口
- 4sqlserver.jdbc.SQLServerException: 驱动程序无法通过使用安全套接字层(SSL)加密与 SQL Server 建立安全连接_failed to obtain jdbc connection; nested exception
- 5vulnhub靶机渗透 FRISTILEAKS: 1.3_vulnhub: fristileaks安装
- 6AttentionOCR Pytorch中文识别程序_torch bilstm接cnncsdn
- 7(ARM-Linux) ORACLE JDK 22 的下载安装及环境变量的配置_jdk22下载安装
- 8一文详解Softmax函数_python 里的softmax函数的概率代表什么
- 9linux 日常使用命令_跑显存命令
- 10金融业开源软件研究评测（一）——分布式消息中间件评测模型_金融业开源软件评测
当前位置: article > 正文
射影几何 -- 空间射影几何 2_几个点确定一个二次曲面
作者：weixin_40725706 | 2024-06-26 11:47:27
赞
踩
几个点确定一个二次曲面
三维射影变换
三维射影变换是射影空间上的可逆齐次线性变换，这个变换可由
4
×
4
的矩阵
H 来描述：X
′ =
H
X
矩阵
H 称为射影变换矩阵或称为单应矩阵。三维射影变换有
15
个自由度
5 点确定三维射影变换：如果
5
个点对应中任意
4
点不共面，则它们唯一确定一个三维射影变换
平面与直线的变换规则
射影变换 H 对平面的变换规则是
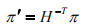
射影变换
H
对直线 L 的变换规则是
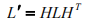
其对偶形式是：
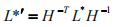
二次曲面与变换规则
二次曲面方程所定义：
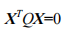，其
中
Q
是
4
×
4 的对称矩阵
，其
中
Q
是
4
×
4 的对称矩阵
如果
Q
是降秩的，则称它为退化二次曲面，否则称为非退化二次曲面
二次曲面的一些常用性质：
1． 二次曲面有
9
个自由度，即由它的
10
个不同元素的比值所确定，因此空间中
9 个点可确 定一个二次曲面；如果二次曲面是退化的，则可用较少的点来确定；
2． 直线与二次曲面交于两个点
(
可能是重点或虚点
)
；
3． 平面
π
与二次曲面
Q
的交是一条二次曲线；
4． 在一般情况下，两个二次曲面的交是一条空间
4 次曲线。如果两个二次曲面都是锥面，则 它们的交线由两条二次曲线所构成。
5． 对于非退化的二次曲面
Q
上的每一点
X
都存在切平面
π
，切平面的坐标由
π
=Q
X 给出； 如果平面
π
是切平面，则切点
X 的坐标由
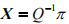给出。锥面 Q 在顶点处不存在切平面， 其他任何一点
X
都存在切平面
π
，切平面的坐标也由
π
=QX。与非退化二次曲面不同的是锥面同一条母线上的点有相同的切平面，也就是说给定锥面的切平面不能唯一确定它的切点。
给出。锥面 Q 在顶点处不存在切平面， 其他任何一点
X
都存在切平面
π
，切平面的坐标也由
π
=QX。与非退化二次曲面不同的是锥面同一条母线上的点有相同的切平面，也就是说给定锥面的切平面不能唯一确定它的切点。
给定一个二次曲面
Q
，则
π
=Q
X 确定了空间点与平面的的一个对应关系，通常称为由二次曲面
Q 的配极对应。如果二次曲面
Q 是非退化的，则它的配极对应是点与平面之间的一一对应。在几何上，如果点
X 在二次曲面
Q 上，则它的极平面是点
X 的切平面；如果点
X 不在(非退化)二次曲面
Q 上，则点
X 的极平面是以
X 为顶点的锥面与
Q 的切点所在的平面
在射影变换
X
′
=HX 下，二次曲面变换规则是：
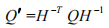
空间曲面的对偶是指以该曲面的切平面为基本元素在对偶空间
(
面空间)中所构成的曲面，通常 称对偶曲面Q
*
。
在一般情况下，二次曲面的对偶仍为一个二次曲面。
Q
是
Q
*
中的所有平面所形成的包络
非退化二次曲面的对偶
Q
* 仍是二次曲面，并且
。
。
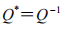锥面的对偶是一条平面曲线
锥面
Q 的对偶在对偶空间中是一条二次曲线，这条二次曲线的支撑面是锥面顶点的对偶，锥面
Q
的母线在对偶空间中被压缩为二次曲线上的一个点。锥面
Q 的对偶可以用下述方程来描述：
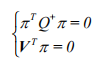
空间二次曲线的对偶曲面是一个锥面，二次曲线的支撑平面的对偶是这个锥面的顶点，二次曲线上的一个点在对偶空间中被扩展为锥面的一条母线，二次曲线的切线与锥面的母线构成一一对应关系。
对偶二次曲面的变换规则
在
(
点
)
变换
X
′
=H
X 下，应用平面的变换规则
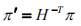，立即得到对偶二次曲面Q *的变换规则：
，立即得到对偶二次曲面Q *的变换规则：
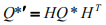
锥面的对偶曲面
Q
* 是一条空间二次曲线，可以由对偶锥面和平面的变换规则来联合表达：
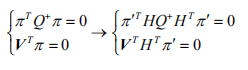
绝对二次曲线
绝对二次曲线
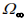是
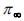上的一条
(
点)二次曲线。在欧氏坐标系下
，
是
上的一条
(
点)二次曲线。在欧氏坐标系下
，
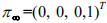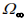
是下述方程的解集：
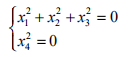
它是
上的一条虚二次曲线。尽管
没有实点，但它具有二次曲线的共同性质
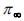上的一条虚二次曲线。尽管
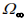没有实点，但它具有二次曲线的共同性质
性质：
三维射影空间中，令
d
1
和
d
2
是两条直线与二次曲线
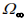所在平面
的交点，它表示这两条直线在射影空间中的方向。
是绝对二次曲线在平面
上的矩阵表示。则两条直线交角可以通过下述公式来计算：
所在平面
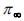的交点，它表示这两条直线在射影空间中的方向。
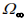是绝对二次曲线在平面
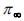上的矩阵表示。则两条直线交角可以通过下述公式来计算：
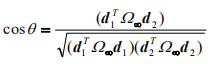
绝对二次曲线
的对偶是三维空间中的退化对偶二次曲面，称它为绝对二次曲面并记为
。
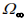的对偶是三维空间中的退化对偶二次曲面，称它为绝对二次曲面并记为
。
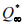在三维射影空间中，若绝对二次曲面的矩阵表示为
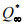，则两平面
π
1
和
π
2 之间的夹角由下式给出：
，则两平面
π
1
和
π
2 之间的夹角由下式给出：
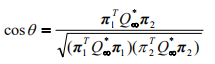
特别地，在欧氏空间中，若两平面的坐标
，则两平面的夹角计算公式简化为：
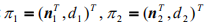，则两平面的夹角计算公式简化为：
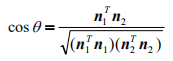
令
Q
r
是中心在原点半径 r 为的球面，则它的矩阵表示为
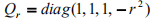
即球面
Qr 上的点
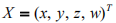满足方程：
满足方程：
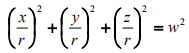
可以将绝对二次曲线作为球面
Q
r
在
r
→ ∞ 时的极限。
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/759256
推荐阅读
相关标签
