weixin_40725706

这个屌丝很懒，什么也没留下！

热门标签

排序算法学习（Java）详解_stdrandom web import

作者：weixin_40725706 | 2024-02-07 21:13:29

踩

stdrandom web import

目录

模板

方法模板

输入Demo

选择排序

代码

输出

插入排序

代码

输出

希尔排序

代码

输出

数据生成器

测试数据集

归并排序

代码

归并过程

快速排序

快排过程

代码

模板

为了快速实现算法，我们首先定义一些模板：

方法模板


package Algorithms_FE.Sort;
 
public class Demo {
  //检查a是否小于b
    public static boolean less(Comparable a, Comparable b){
        return a.compareTo(b)<0;
    }
    //交换数组a中, b c 索引的值
    public static void swap(int[] a, int b, int c){
        int tmp=a[b];
        a[b]=a[c];
        a[c]=tmp;
 
    }
    //打印数组情况
    public static void show(int[] a){
        for (int i = 0; i < a.length; i++) {
            System.out.print(a[i]+" ");
        }
        System.out.println();
    }
    //检查数组元素是否有序
    public static boolean isSorted(int[] a){
        for (int i = 1; i < a.length; i++) {
            if(less(a[i],a[i-1])) return false;
        }
        return true;
    }
 
 
}

排序代码对实现 Java 的 Comparable接口的任何类型的数据都有效，但只能是是同一种数据类型的排序(你可以对int double char等数据类型排序，但你不能同时出现不同的数据类型）。下面我们用int类型举例：

输入Demo


10
8 6 2 8 5 0 3 7 2 2

选择排序

首先找到数组中最小的元素，其次，将它和数组中第一个元素交换位置（如果第一个元素就是最小元素那么它就和自己交换）。再次在剩下的元素中找到最小的元素与数组第二个元素交换位置，如此往复，直到将整个数组排序。

代码

这里注意一下要提前导入写好的模板，使用里面的方法。


package Algorithms_FE.Sort;
 
import java.io.BufferedInputStream;
import java.util.Scanner;
 
import static Algorithms_FE.Sort.Demo.*;
 
 
public class Select_sort {
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        while (in.hasNext()) {
            int n=in.nextInt();
            System.out.println("number:"+n);//需要排序的元素数量
            int[]a=new int[n];
            for (int i = 0; i < n; i++) {
                a[i]=in.nextInt();
            }
            System.out.println("before:");
            show(a);
            System.out.println("sorting:");
            long start=System.currentTimeMillis();
            for (int i = 0; i < a.length; i++) {
                int min=i;//最小元素索引
                for (int j = i+1; j < n; j++) {
                    if(less(a[j],a[min])){//如果小于
                        min = j;
                    }
                }
                swap(a,i,min);//交换
                System.out.println(min+" -> "+i);
            }
            long end=System.currentTimeMillis();
            System.out.println("after:");
            show(a);
            long cost=end - start;
            System.out.println(cost+"ms");
 
        }
    }
}

输出

这里我们可以看到索引改变情况：


number:10
before:
8 6 2 8 5 0 3 7 2 2 
sorting:
5 -> 0
2 -> 1
8 -> 2
9 -> 3
6 -> 4
6 -> 5
8 -> 6
7 -> 7
8 -> 8
9 -> 9
after:
0 2 2 2 3 5 6 7 8 8 
7ms

插入排序

人们整理扑克牌的方法是一张一张来，将每一张牌插入到其他有序牌里的适当位置。计算机实现需要给插入的元素腾出空间，要把其他所有元素在插入之前都向右移动一位。这种方法叫做插入排序。

代码


package Algorithms_FE.Sort;
 
import java.util.*;
import java.io.*;
 
import static Algorithms_FE.Sort.Demo.*;
 
public class Insert_sort {
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        while (in.hasNext()) {
            int n=in.nextInt();
            System.out.println("number:"+n);//需要排序的元素数量
            int[]a=new int[n];
            for (int i = 0; i < n; i++) {
                a[i]=in.nextInt();
            }
            System.out.println("before:");
            show(a);
            System.out.println("sorting:");
            long start=System.currentTimeMillis();
            for (int i = 1; i < n; i++) {
                for (int j = i; j >0; j--) {
                    if(less(a[j],a[j-1])){
                        swap(a,j,j-1);
                        System.out.println(j+" -> "+(j-1));
                    }
 
                }
            }
            long end=System.currentTimeMillis();
            System.out.println("after:");
            show(a);
            long cost=end - start;
            System.out.println(cost+"ms");
 
 
        }
    }
}

输出

这里因为要不断移动元素，所以操作较为频繁。


number:10
before:
8 6 2 8 5 0 3 7 2 2 
sorting:
1 -> 0
2 -> 1
1 -> 0
4 -> 3
3 -> 2
2 -> 1
5 -> 4
4 -> 3
3 -> 2
2 -> 1
1 -> 0
6 -> 5
5 -> 4
4 -> 3
3 -> 2
7 -> 6
6 -> 5
8 -> 7
7 -> 6
6 -> 5
5 -> 4
4 -> 3
3 -> 2
9 -> 8
8 -> 7
7 -> 6
6 -> 5
5 -> 4
4 -> 3
after:
0 2 2 2 3 5 6 7 8 8 
15ms

希尔排序

基于插入排序的快速排序算法，对于大规模乱序数组插入排序会很慢，因为它只能交换相邻的元素，元素只能一点点地从数组地一端移动到另一端。

希尔排序的思想是使数组中任意间隔为h的元素是有序的。这样的数组称为h有序数组。一个h有序数组就是h个相互独立的有序数组编织在一起的数组。如果h很大，我们就能将元素移动到很远的地方，为了实现更小的h有序创造方便。下面算法使用了序列 $1/2(3^{k}-1)$ ,从n/3开始递减为1。

实现希尔排序的方法是对每个h，用插入排序将h个子数组独立的排序。

希尔排序更加高效的原因是它权衡了子数组的规模和有序性。起初，各个子数组之间都很短，排序之后子数组部分有序。子数组部分有序的程度取决于递增序列的选择。透彻理解希尔排序性能至今仍是一项挑战。

代码：


package Algorithms_FE.Sort;
 
import java.io.BufferedInputStream;
import java.util.Scanner;
 
import static Algorithms_FE.Sort.Demo.*;
 
public class Shell_sort {
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        while (in.hasNext()) {
            int n=in.nextInt();
            System.out.println("number:"+n);//需要排序的元素数量
            int[]a=new int[n];
            for (int i = 0; i < n; i++) {
                a[i]=in.nextInt();
            }
            System.out.println("before:");
            show(a);
            System.out.println("sorting:");
 
            int h=1;
            while (h<n/3){
                h=h*3+1;
            }
            long start=System.currentTimeMillis();
            while (h>=1){
                for (int i=h;i<n;i++){
                    for (int j=i;j>=h&&less(a[j],a[j-h]);j-=h){
                            swap(a,j,j-h);
                            System.out.println(j+" -> "+(j-h)+" ");
                    }
                    System.out.println();
                }
                h=h/3;
            }
            long end=System.currentTimeMillis();
            System.out.println("after:");
            show(a);
            long cost=end - start;
            System.out.println(cost+"ms");
 
 
 
        }
    }
}

输出


number:10
before:
8 6 2 8 5 0 3 7 2 2 
sorting:
4 -> 0 
 
5 -> 1 
 
 
7 -> 3 
 
8 -> 4 
4 -> 0 
 
9 -> 5 
 
1 -> 0 
 
 
 
4 -> 3 
 
5 -> 4 
4 -> 3 
 
6 -> 5 
5 -> 4 
 
 
 
9 -> 8 
8 -> 7 
7 -> 6 
 
after:
0 2 2 2 3 5 6 7 8 8 
16ms

和插入排序的比较性能的比较：

首先测试输入Demo之后的比较：

由于数据集较小，且时间相差并不大，性能比较并不明显。

这里我写了一个随机数据生成器，使用算法第四版的标准库（需要的同学可在Prim这篇文章里下载），它能生成 $10*n$ 的数据在[0-100）之间的数据集：

数据生成器


 
package Algorithms_FE.Sort;
 
import edu.princeton.cs.algs4.StdRandom;
 
import java.io.BufferedInputStream;
import java.util.Scanner;
 
public class DataProducer {
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        int n=in.nextInt();
        for (int i = 0; i < n; i++) {
            for (int j = 0; j < 10; j++) {
                System.out.print(StdRandom.uniformInt(100)+" ");
            }
            System.out.println();
        }
    }
}

现在我们输入100，生成1000个数据单位，让这两个不同的算法进行排序，查看其性能：

测试数据集

测试数据集里的首位要变成1000，因为是1000个数据集


1000
98 51 9 77 61 82 78 69 32 56 
33 72 84 16 37 30 86 52 38 3 
46 89 30 45 26 23 21 5 93 74 
83 67 11 64 18 7 29 95 6 69 
87 13 42 32 95 55 18 47 45 71 
44 48 9 88 44 55 48 61 14 23 
26 65 98 96 26 22 52 1 0 59 
32 40 41 96 93 1 65 2 10 88 
85 93 68 20 84 92 94 16 11 27 
88 24 58 2 51 14 11 97 0 91 
61 27 60 82 58 22 31 74 62 47 
84 80 20 87 40 72 96 57 20 30 
83 97 6 47 74 11 53 21 42 2 
65 4 37 72 29 25 30 6 11 57 
71 48 26 63 40 80 23 67 45 25 
98 16 68 96 97 97 45 30 39 65 
15 68 47 5 16 12 28 90 90 25 
29 64 44 51 14 85 68 96 17 11 
46 19 55 34 43 7 40 6 69 84 
46 54 30 55 30 53 88 48 25 34 
20 82 33 35 0 50 97 78 47 28 
79 61 40 54 89 56 50 39 75 61 
70 17 42 36 39 84 19 1 56 80 
32 52 65 37 32 11 80 70 31 59 
71 3 32 4 34 96 18 15 18 83 
26 23 77 94 35 96 2 55 9 13 
50 88 40 76 77 47 1 12 83 23 
79 58 10 94 0 2 32 75 71 45 
67 40 94 0 81 5 44 52 8 34 
68 84 34 72 82 62 69 8 96 2 
82 45 6 29 6 16 55 44 28 21 
63 40 26 97 58 67 35 50 54 6 
19 48 57 8 97 40 22 30 91 26 
74 80 96 8 32 35 98 69 54 37 
51 92 20 11 29 18 50 85 95 27 
61 53 72 6 3 14 43 83 64 4 
96 31 58 19 54 48 5 52 66 18 
12 99 20 65 16 74 89 20 38 66 
28 75 73 57 39 62 58 97 75 43 
36 85 45 7 64 90 71 40 57 76 
13 74 5 27 37 32 24 17 59 42 
39 1 87 54 94 59 17 0 27 63 
65 38 9 80 52 81 76 66 4 74 
43 71 69 50 66 28 58 61 92 0 
65 25 24 67 39 11 55 69 64 42 
64 21 23 14 36 24 55 29 83 23 
76 28 65 34 69 81 6 79 60 0 
59 51 1 88 17 60 52 84 97 9 
13 59 43 90 2 13 1 11 88 40 
92 68 32 56 65 96 9 59 25 88 
2 1 59 75 13 39 31 35 64 3 
80 81 49 20 56 3 0 64 76 45 
85 25 43 63 59 52 12 40 85 93 
59 90 53 3 6 75 11 95 53 9 
24 9 64 47 38 19 17 24 5 87 
20 4 12 64 25 21 86 93 65 24 
93 66 5 6 77 52 37 19 29 55 
51 38 90 42 40 26 38 88 12 68 
24 26 75 13 47 38 88 73 1 63 
77 32 85 83 38 12 57 2 11 83 
45 4 5 13 2 30 65 43 59 66 
96 68 18 41 23 33 12 38 70 17 
7 86 5 54 61 23 10 79 1 63 
78 95 58 25 36 7 36 9 27 16 
99 85 37 68 18 84 85 19 41 77 
71 9 80 10 31 63 25 98 30 4 
66 1 16 31 19 66 63 43 54 91 
58 38 32 45 8 99 41 75 72 15 
45 58 29 63 18 87 47 32 97 61 
77 67 76 5 54 80 90 40 82 63 
43 52 54 90 76 51 64 78 39 22 
38 1 87 18 50 29 2 13 83 64 
13 79 67 39 62 11 4 64 74 30 
38 28 69 32 6 99 5 55 97 1 
3 36 81 81 77 16 53 36 94 59 
49 79 33 33 20 1 81 67 97 69 
98 45 42 45 96 2 75 85 97 92 
48 99 93 87 94 68 38 36 47 3 
94 11 26 33 57 30 1 25 24 85 
47 74 60 64 78 20 21 40 5 0 
35 86 0 45 34 65 21 16 46 55 
27 35 25 55 82 74 33 22 57 74 
88 65 12 59 23 95 42 14 99 72 
76 53 14 46 97 71 77 15 1 59 
85 24 69 20 4 69 16 58 70 70 
72 77 96 55 29 5 31 63 91 70 
63 80 76 30 84 27 67 88 27 97 
39 16 79 88 77 97 14 55 86 6 
54 74 31 18 33 2 6 50 68 3 
8 54 65 10 72 53 80 81 99 9 
40 7 32 87 91 2 88 27 20 42 
26 41 26 32 88 84 18 72 22 28 
94 8 33 75 16 19 77 68 98 33 
48 86 35 81 97 48 87 66 73 82 
1 14 25 79 83 10 53 56 4 63 
62 34 17 65 63 92 9 7 15 97 
5 91 14 90 33 43 57 79 34 65 
44 41 50 11 63 40 11 28 26 38 
14 36 30 28 41 43 8 19 23 30 
17 7 31 17 42 10 97 57 59 21

这样就可以直观明了的对比算法性能时间。

最后再让我们看看选择排序的表现：

（Ohhhh！）（我本以为希尔已经天下无敌了，没想到竟然有人比它还勇猛，这是谁的部下）

归并排序

归并排序基于归并这个操作，即将两个有序数组归并成一个更大的有序数组。归并排序可以先递归地将它分成两半分别排序，然后将结果归并起来。

实现归并排序的一种直接的方法就是将两个不同的有序数组归并到第三个数组中。但是使用归并将一个很大的数组排序时，我们需要多次归并，每次都生成一个新数组来存储结果会存在问题。我们希望能够在原地进行归并，先将前半段进行排序，然后再将后半段排序。

代码


package Algorithms_FE.Sort;
 
import java.util.*;
import java.io.*;
 
import static Algorithms_FE.Sort.Demo.less;
import static Algorithms_FE.Sort.Demo.show;
 
public class Merge_sort {
    public static int[]aux;//辅助数组
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        while (in.hasNext()) {
            int n=in.nextInt();
            System.out.println("number:"+n);//需要排序的元素数量
            int[]a=new int[n];
            aux=new int[n];
            for (int i = 0; i < n; i++) {
                a[i]=in.nextInt();
            }
            System.out.println("before:");
            show(a);
            long start=System.currentTimeMillis();
            sort(a,0,a.length-1);
            long end=System.currentTimeMillis();
            System.out.println("after:");
            show(a);
            long cost=end - start;
            System.out.println(cost+"ms");
 
 
        }
    }
    public static void sort(int[]a,int lo,int hi){
        if(hi<=lo)return;
        int mid=(lo+hi)>>1;
        sort(a,lo,mid);
        sort(a,mid+1,hi);
        merge(a,lo,mid,hi);
    }
    public static void merge(int[]a,int lo,int mid ,int hi){
        //a[lo-mid]和a[mid+1-hi]归并在一起
        int i=lo,j=mid+1;
        for (int k=lo;k<=hi;k++){//将a[lo-hi]复制到aux[lo-hi]
            aux[k] = a[k];
        }
        for (int k =lo; k <=hi ; k++) {
            if(i>mid) a[k]=aux[j++];
            else if (j>hi) {
                a[k]=aux[i++];
            } else if (less(aux[j],aux[i])) {
                a[k]=aux[j++];
            }else {
                a[k]=aux[i++];
            }
 
        }
    }
 
}

归并过程

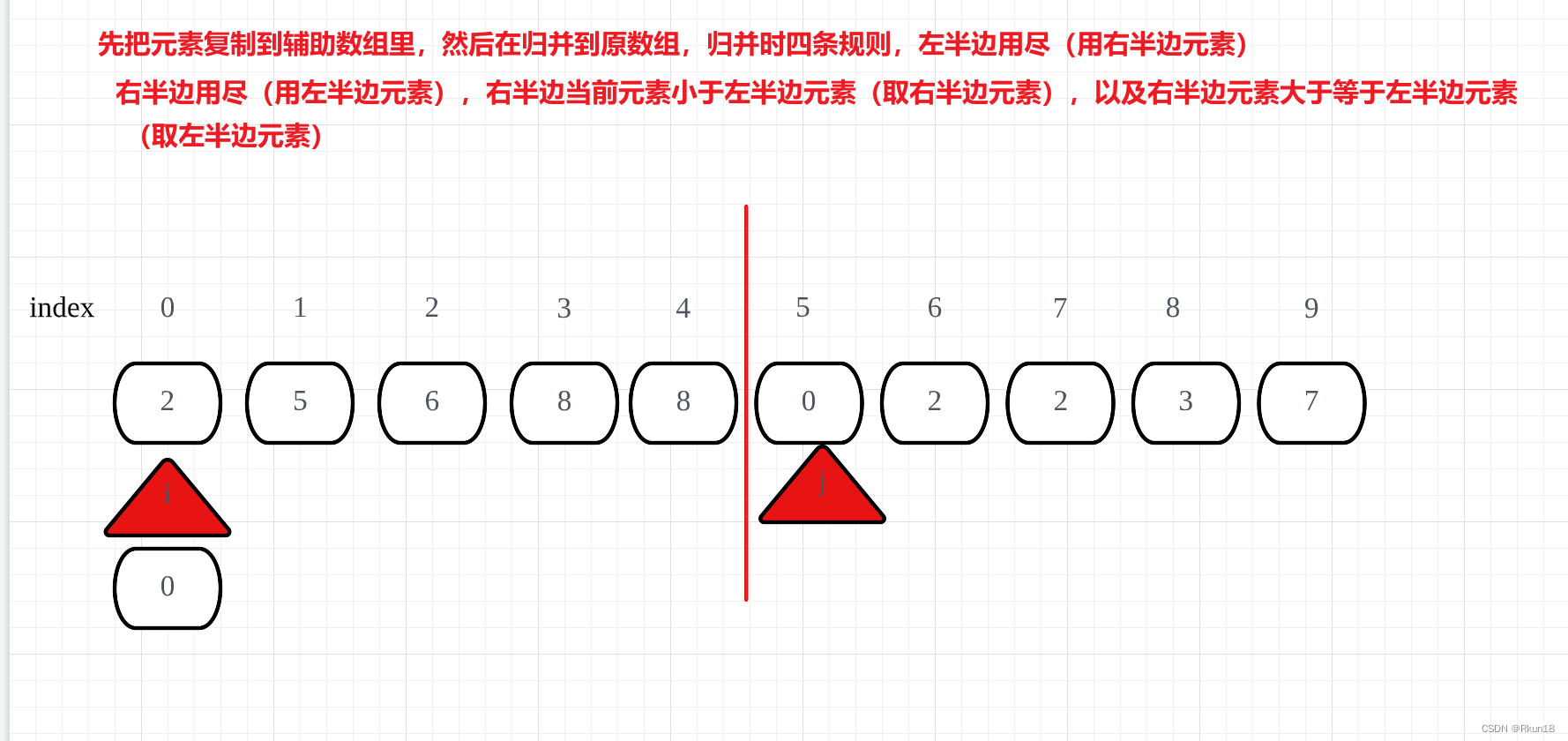
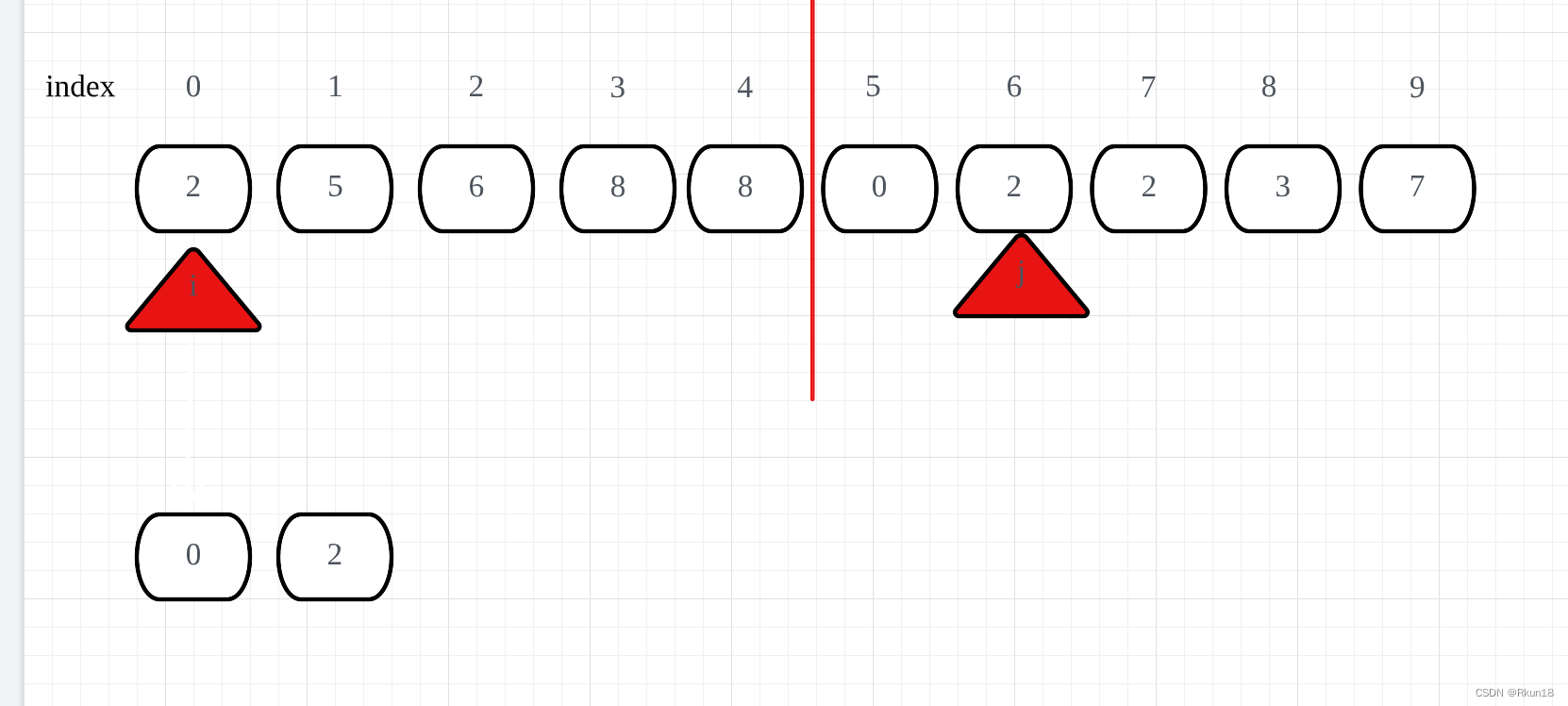
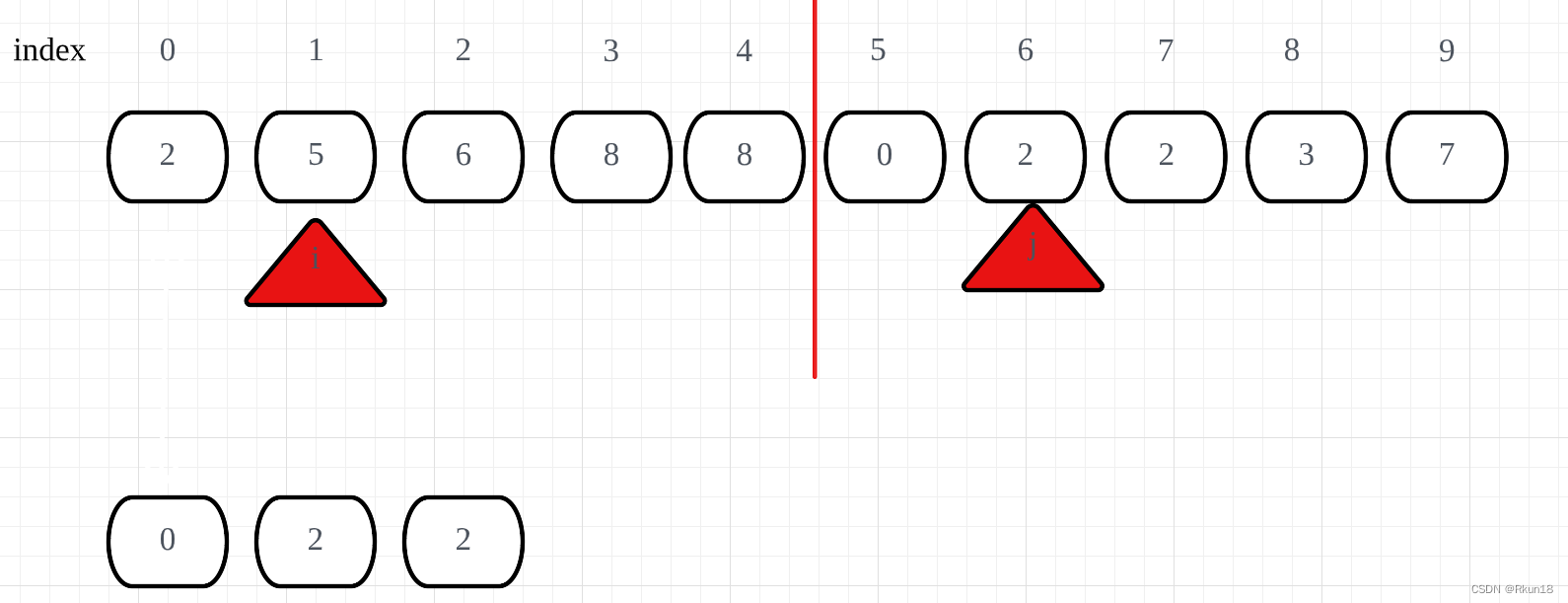
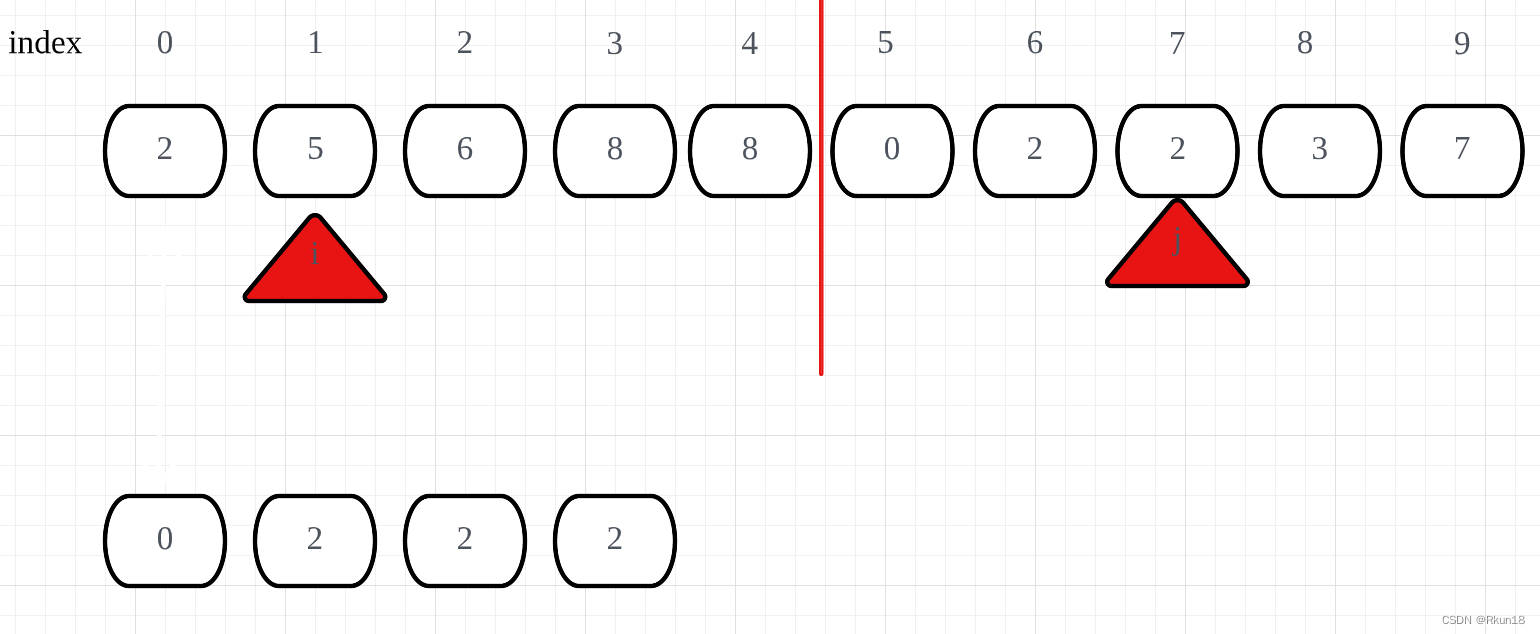
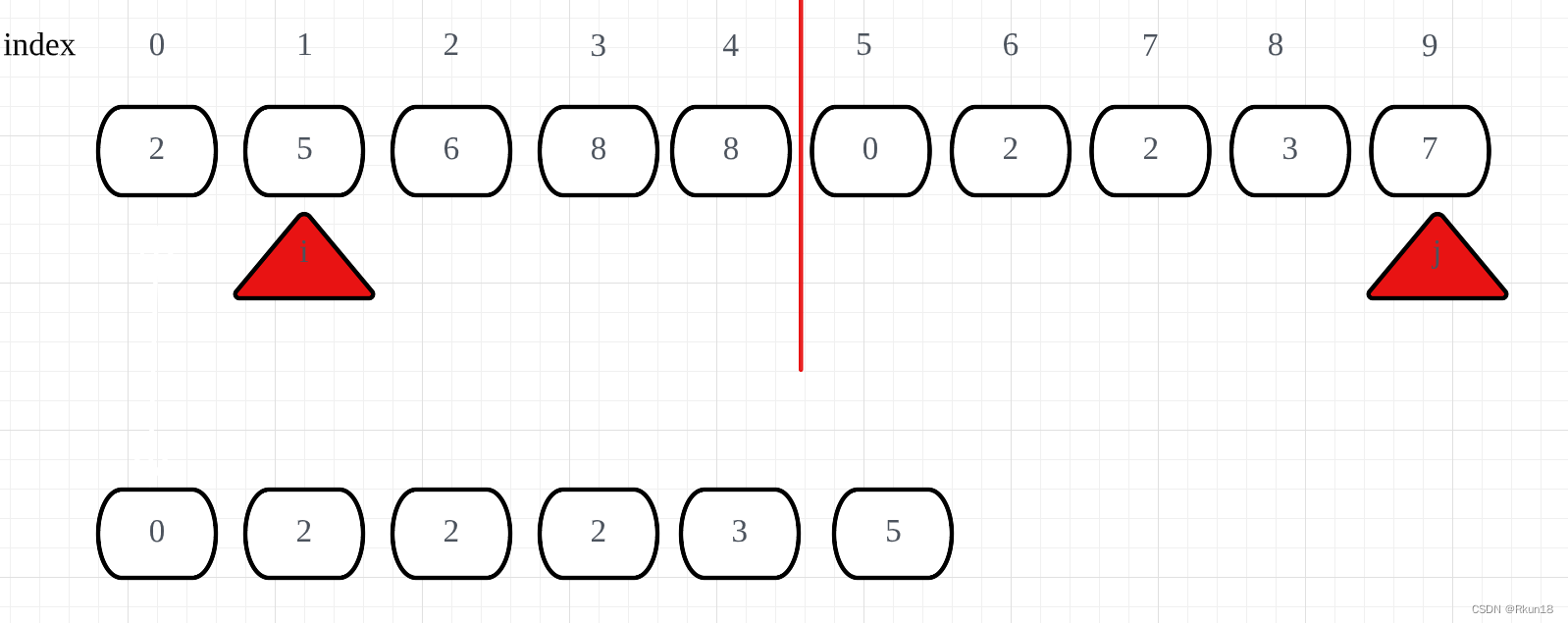
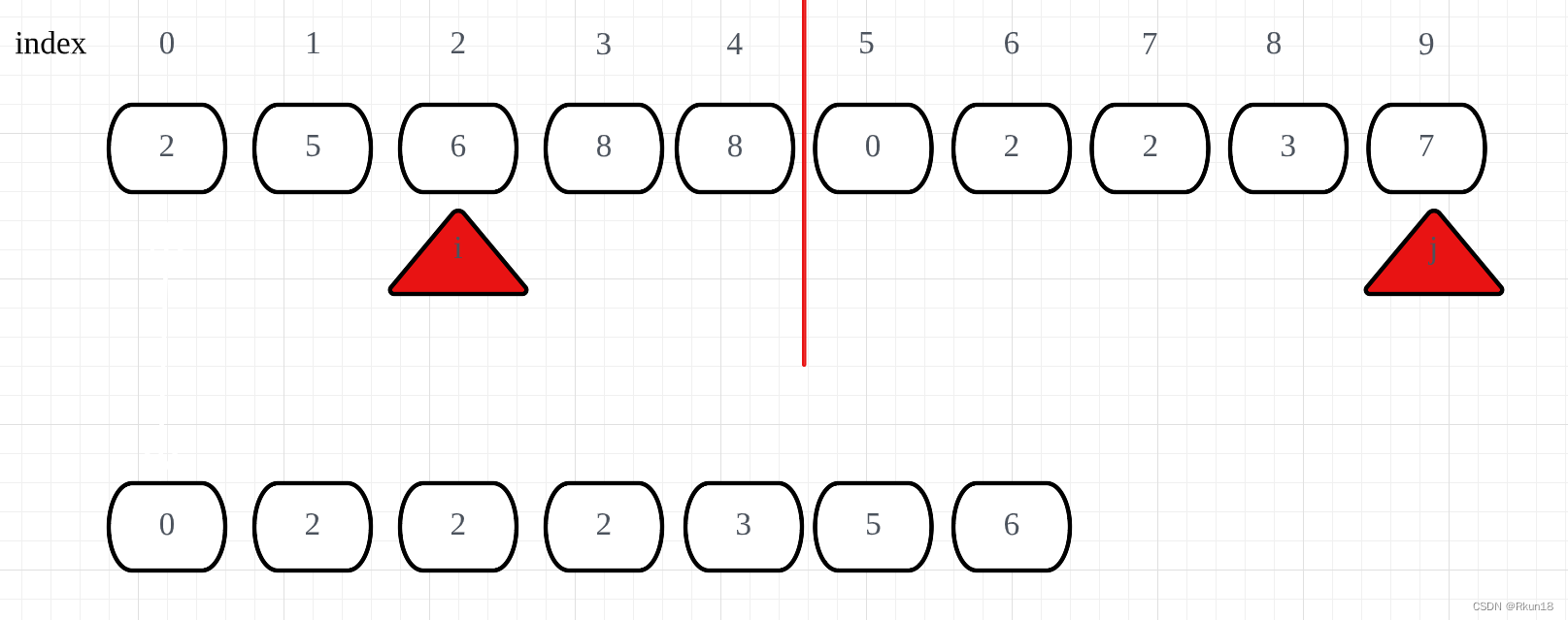
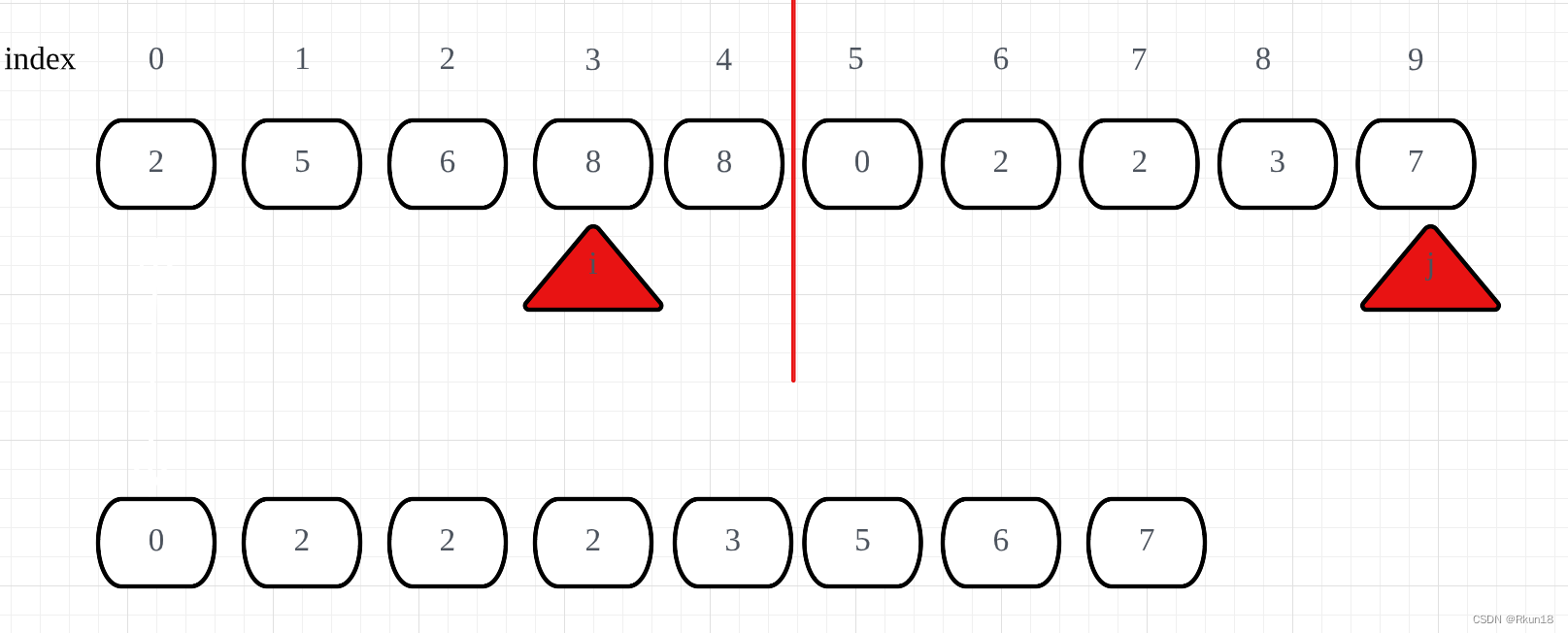
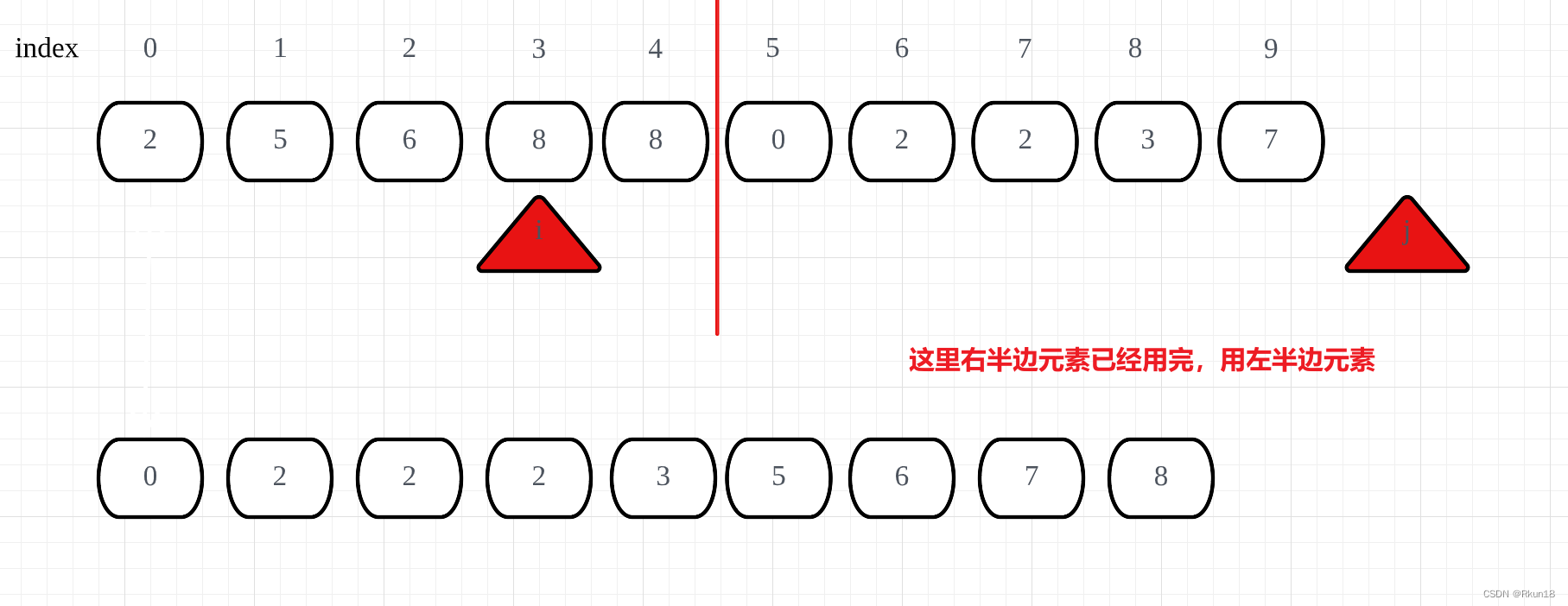
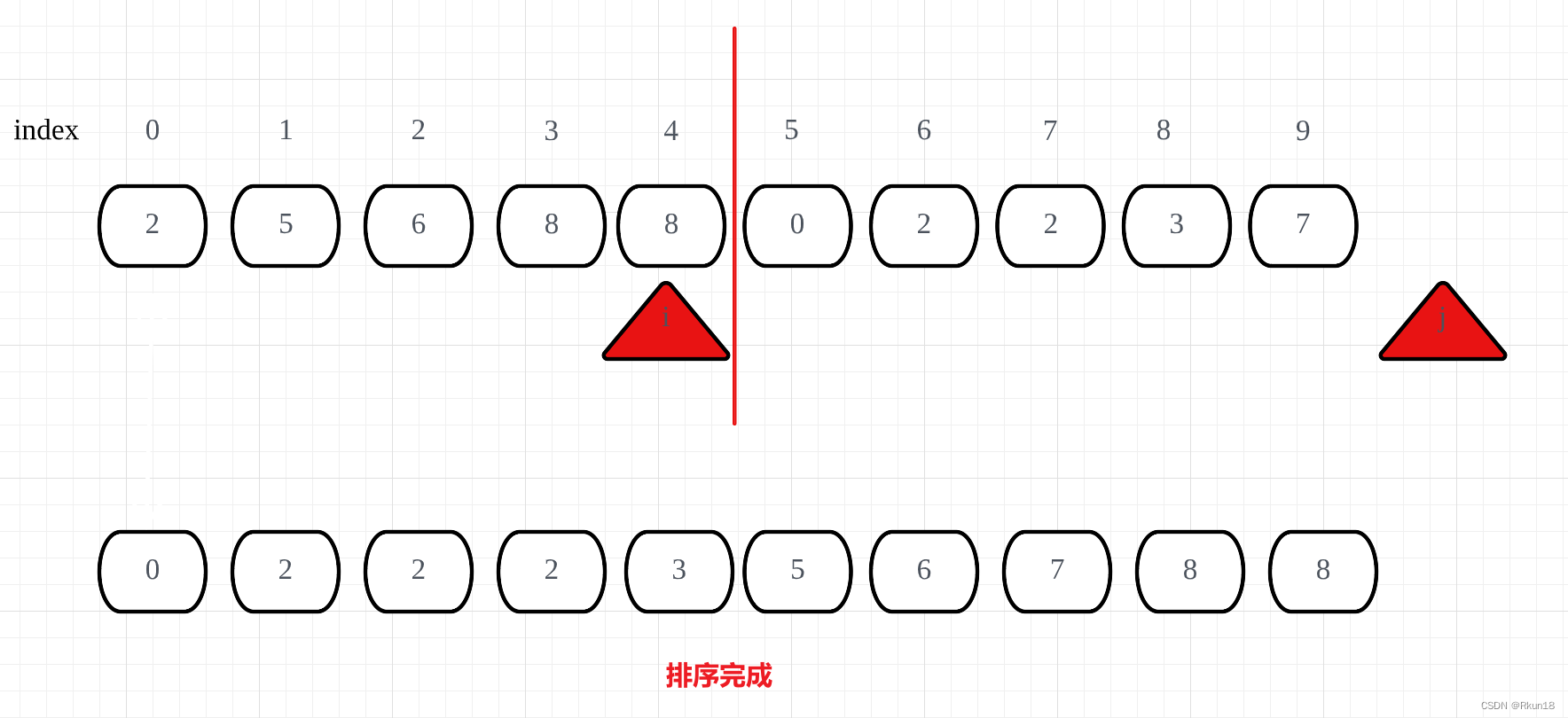
同时输入相同的输入Demo和数据集，比较算法性能：

快速排序

快速排序可能是应用最广泛的排序算法了，因为它实现简单，适用于适用于不同输入数据且算法性能要比其他排序算法要更好。快速排序的内循环要比大多数排序算法要小，意味着理论和实际中都要更快。缺点是较为脆弱，实现时要比较小心才能避免低性能。

快速排序是一种分治的排序算法，将一个数组分成两部分，两部分独立地排序。

快排过程

从数列中挑出一个元素，称为 "基准"（pivot）;

重新排序数列，所有元素比基准值小的摆放在基准前面，所有元素比基准值大的摆在基准的后面（相同的数可以到任一边）。在这个分区退出之后，该基准就处于数列的中间位置。这个称为分区（partition）操作；

递归地（recursive）把小于基准值元素的子数列和大于基准值元素的子数列排序。

代码


package Algorithms_FE.Sort;
 
import java.util.*;
import java.io.*;
 
import static Algorithms_FE.Sort.Demo.*;
 
public class Quick_sort {
    public static void main(String[] args) {
        Scanner in = new Scanner(new BufferedInputStream(System.in));
        while (in.hasNext()) {
            int n=in.nextInt();
            System.out.println("number:"+n);//需要排序的元素数量
            int[]a=new int[n];
            for (int i = 0; i < n; i++) {
                a[i]=in.nextInt();
            }
            System.out.println("before:");
            show(a);
            long start=System.currentTimeMillis();
            int[]b=quickSort(a,0,a.length-1);
            long end=System.currentTimeMillis();
            System.out.println("after:");
            show(b);
            long cost=end - start;
            System.out.println(cost+"ms");
 
 
        }
    }
    private static int[] quickSort(int[] arr, int left, int right) {
        if (left < right) {
            int partitionIndex = partition(arr, left, right);
            quickSort(arr, left, partitionIndex - 1);
            quickSort(arr, partitionIndex + 1, right);
        }
        return arr;
    }
 
    private static int partition(int[] arr, int left, int right) {
        // 设定基准值（pivot）
        int pivot = left;
        int index = pivot + 1;
        for (int i = index; i <= right; i++) {
            if (arr[i] < arr[pivot]) {
                swap(arr, i, index);
                index++;
            }
        }
        swap(arr, pivot, index - 1);
        return index - 1;
    }
}

同时输入相同的输入Demo和数据集，比较算法性能：

用数据生成器再生成一个数据元素为10000的数据集测试：

可以看到快排的性能。

声明：本文内容由网友自发贡献，转载请注明出处：【wpsshop】