weixin_40725706

这个屌丝很懒，什么也没留下！

热门标签

C++中二叉搜索树的模拟实现(二叉搜索树是map,set的底层原理)

作者：weixin_40725706 | 2024-04-07 20:40:17

踩

搜索二叉树

定义

搜索二叉树:左子树小于根,右子树大于根.搜索二叉树的中序序列是升序的.所以对于二叉树而言,它的左子树和右子数都是二叉搜索树

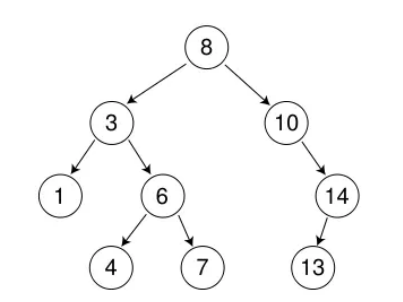
下图就是二叉搜索树
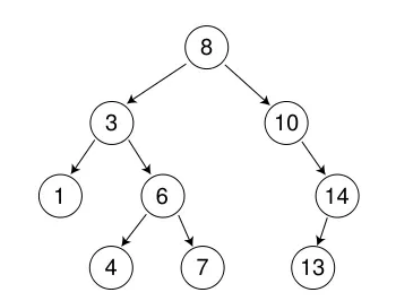
在这里插入图片描述

二叉搜索树的性质:

二叉搜索树的中序遍历出的数据是有序的,并且二叉树搜索树在查找某个数的时候,一般情况下的时间复杂度是O(log₂(N))级别的.
二叉搜索树中是没有值相同的节点的,否则无法构成二叉搜索树.

节点的定义

二叉树和别的树的区别就是各个节点的排列有了区别,节点中存储的内容还是不会变的,仍然是左右指针,和一个值.

template<class K>
struct BinarySearchTreeNode
{
	typedef BinarySearchTreeNode<K> Node;
	Node* _left;
	Node* _right;
	K _key;
	BinarySearchTreeNode(const K& key)
        : _left(nullptr)
        , _right(nullptr)
        , _key(key){}
};
1
2
3
4
5
6
7
8
9
10
11
12

节点的构造方法

	BinarySearchTreeNode(const K& key)
        : _left(nullptr)
        , _right(nullptr)
        , _key(key){}
1
2
3
4

二叉搜索树的创建

二叉搜索树的创建首先只需要一个根节点即可,后续插入节点或者删除节点时,保持住连接关系就好.

template<class T>
class BinarySearchTree
{
	typedef BinarySearchTreeNode<K> Node;
	private:
	Node* _root = nullptr;
	public:
	// 各种函数
};
1
2
3
4
5
6
7
8
9

注意:后边的这些方法都是写在类的public中的.

向树中插入节点

例如:插入节点A的时候,要判断A中的key值和树中根节点开始,依次比较key值,我们定义一个cur指针,用于为新来的节点找到合适的插入位置,假如A节点的key值<cur节点的key值,那么就cur就向左树开始遍历.假如A的key值和cur的key值相同,直接返回.假如A的key值大于cur的key值,cur就向右数遍历.最终cur的位置就是能插入数据的地方,但是cur的值最后是为空的,那么我们如何将cur处的值替换为这个A节点呢?换句话说,如何让cur的父节点指向这个A节点呢?答案是:我们在cur向下一个节点行进之前,先保存当前节点的指针,也就是保存好cur的父节点的值.

但是A节点最终是链接在父节点的左边还是在父节点的右边呢??这个只能通过保存的父节点中保存的值进行判断.若A节点的值小于父节点,那么就链接在父节点的左边,否则链接在父节点的右边.
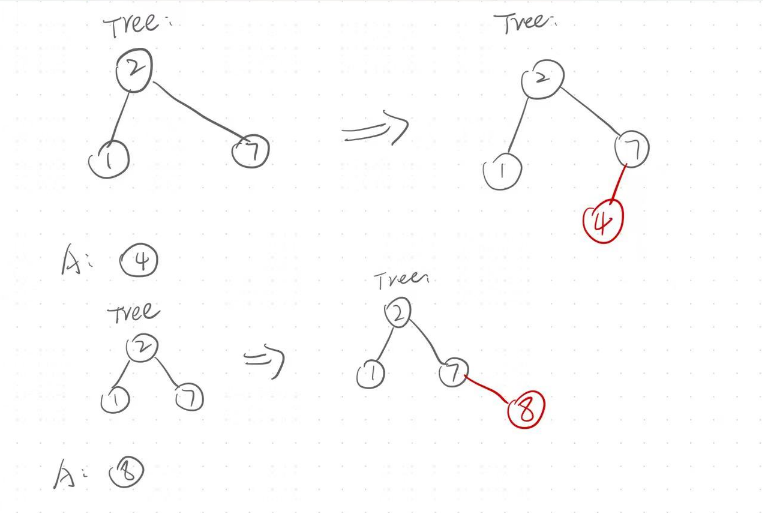
在这里插入图片描述

代码实现:

bool insert(const K& key)
{
	// 插入节点之前,检查是不是空树
	if(_root == nullptr)
	{
		_root = new Node(key);
		return true;
	}
	Node* cur = _root;
	Node* parent = _root;
	while(cur)
	{
        if(key<cur->_key)
        {
        	parent = cur;
            cur = cur->_left;
        }
        else if(key>cur->_key)
        {
        	parent = cur;
        	cur = cur->_right;
        }
        else
        {
        	// 值不能相同直接返回
        	return false;
        }
    }
        if(parent->_key<key)
        {
        	parent->_left = new Node(key);
        }
        else
        {
        	parent->_right = new Node(key);
        }
        return true;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38

查找元素

查找元素就比较简单了,要查找的值小于cur的当前值,那么就向左树查找,若大于当前值,就向右数查找.

代码实现:

bool find(const K& key)
{
	Node* cur = _root;
	while(cur)
	{
		if(key<cur->_key)
        {
			cur = cur->_left;		
        }
        else if(key>cur->_key)
        {
        	cur = cur->_right;
        }
        else
        {
        	return true;
        }
	}
	return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

删除元素

二叉搜素树中,删除节点是最比较复杂的.分为了3种情况

要被删除的目标节点的左树是空:每次cur指针在找目标节点时,每次cur迭代之前,都需要记录cur的当前位置,也就是用parent指针来记录.

当删除的节点是parent的右边时:就需要parent的右指针指向目标节点的右子树.
当删除的节点是parent的左边时:就需要parent的左指针指向目标节点的右子树.

要被删除的节点的右树是空:每次cur指针在找目标节点时,每次cur迭代之前,都需要记录cur的当前位置,也就是用parent指针来记录.

当删除的节点是parent的右边时:就需要parent的右指针指向目标节点的左子树.
当删除的节点是parent的左边时:就需要parent的左指针指向目标节点的左子树.

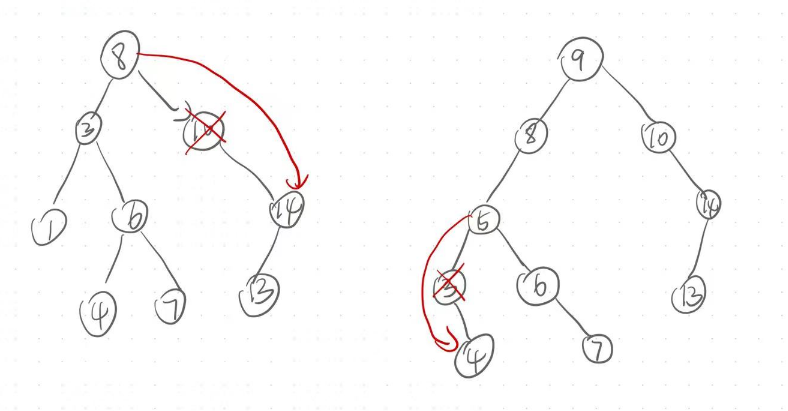
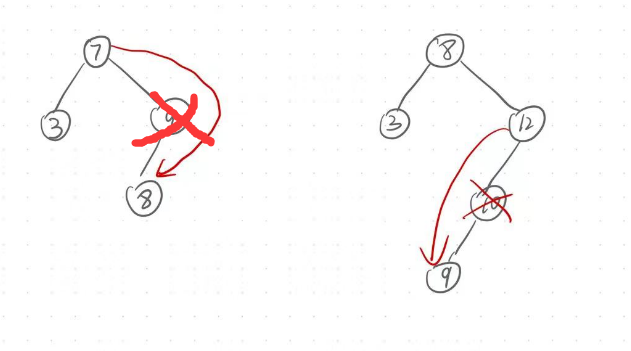
要被删除的节点的左右都不是空的时候:
此时就需要用替换法了,
例如:我们要删除下图中的值为8的节点.删除节点但是不能破环二叉搜索树的结构,所以就需要找到一个值在3和10的节点来替换这里的值为8的节点.那么这值如何找呢?由于二叉搜索树的结构可知,左树的值小于根的值,右树的值总是大于根的值.所以我们可以在左树中找到最大的值或者是在右树中找到最小的值(这两个值的任意一个值都是符合要求的,即大于3小于10的)来替换要被删除节点的位置的值,如下图,就可以将7复制到8这个位置,紧接着删除原本的7所在的节点,就删除成功了.

注意:删除原本值为7的节点时,一定属于第一种和第二种情况之一,因为:左树的最大值的右指针一定为空,右数的最小值的左树一定为空.

代码实现:

bool erase(const K& key)
{
	Node* cur = _root;
	Node* parent = _root;
	while(cur)
	{
		if(key<cur->_key)
		{
			parent = cur;
			cur = cur->_left;
		}
		else if(key>cur->_key)
		{
			parent  = cur;
			cur = cur ->_right;
		}
		else
		{
		// 删除的节点的左树为空
			if(cur->_left == nullptr)
			{
                if(cur == _root)
                {
                    _root = _root->_right;
                }
                else
                {
                    	if(parent->_right == cur)
                        {
                            parent ->_right = cur->_right;
                        }
                        else
                        {
                            parent->_left = cur->_right;
                        }
                }
			
                delete cur;
                return true;
			}
            
			// 删除的节点的右树为空
			else if(cur->_right == nullptr)
			{
                if(cur == _root )
                {
                    _root = _root ->_left;
                }
                else
                {
                    		if(parent->_right == cur)
                            {
                                parent->_right = cur->_left;
                            }
                            else
                            {
                                parent->_left = cur->_left;
                            }
                }
                delete cur;
                return true;
			}
			 // 左右都不为空,替换法
			else
			{
				// 以右边的最小值为例子
				Node* rightMinParent = cur;
				Node* rightMin = cur->_right;
				while(rightMin->_left){
					rightMin = rightMin ->_left;
				}
				cur->_key = rightMin->_key;
				if(rightMinParent->_left == rightMin){
					rightMinParent->_left = rightMin->_right;
				}else
				{
					rightMinParent->_right = rightMin->_right;
				}
				delete rightMin;
				return true;
			}
		}
	}
	return false;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85

二叉树的中序遍历

由于类的成员函数不能递归调用,所以创建一个私有函数_Inorder,接着在public中定义Inorder方法,调用这个_Inorder犯法即可.

void Inorder()
{
    _Inorder(_root);
}
void _Inorder(Node* root)
{
	if(root==nullptr) return;
	_Inorder(root->_left);
	cout<<root->_key<<endl;
	_Inorder(root->_right);
}
1
2
3
4
5
6
7
8
9
10
11

二叉搜索树的递归找数字

bool _Find(Node* root,const K& key)
{
	if(root == nullptr) return false;
	else if(root->_key == key) return true;
	else if (root->_key < key)
    {
        _Find(root->_right, key);
    }
    else
    {
        _Find(root->_left, key);
    }
}
1
2
3
4
5
6
7
8
9
10
11
12
13

二叉搜索树删除元素的另一种方法

这里的root定义成引用即可,root必定是节点的左指针或者右指针的引用.这里直接改变引用的值即可.就不用找父节点了.更方便一点.

		bool _Erase(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}
			if (root->_key < key)
			{
				return _Erase(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _Erase(root->_left, key);
			}
			else
			{
				Node* del = root;
				if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else
				{
					// 替换法
					Node* rightMin = root->_right;
					while (rightMin->_left)
					{
						rightMin = rightMin->_left;
					}
					swap(rightMin->_key, root->_key);
					// 将当前root位置和rightMin位置的值进行交换,接着在root的右边的树中删除key

					return _Erase(root->_right, key);
				}
				delete del;
				return true;
			}
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

二叉搜索树插入数据的第二种方式

// 注意这里的&是不可少的,不然要使用二级指针进行操作了.
		bool _Insert(Node*& root, Node* parent, const K& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
			}
			if (root->_key > key)
			{
				return _Insert(root->_left, parent, key);
			}
			else if (root->_key < key)
			{
				return _Insert(root->_right, parent, key);
			}
			else if (root->_key == key)
			{
				return false;
			}
		}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

二叉搜索树的构造方法

拷贝构造

先拷贝根,再拷贝左右子树

Node* Copy(Node* root)
{
	if(root == nullptr)return nullptr;
	Node* newRoot = new Node(root->_key);
	newRoot->_left = Copy(root->_left);
	newRoot->_right = Copy(root->_right);
	return newRoot;
}
// 在构造函数中:
BinarySearchTree(BinarySearchTree<K>& t){
    this->_root = Copy(t._root);
}
1
2
3
4
5
6
7
8
9
10
11
12

赋值拷贝

注意:要使用如下这种方法,参数必须是类实体,不能是类引用,返回值必须是类引用.

BinarySearchTree<K>& operator=(const BinarySearchTree<K> t)
{
	swap(t._root,this->_root);
	return *this;
}
1
2
3
4
5

默认构造

BinarySearchTree() = default;
1

析构函数

先写一个destroy函数

~BinarySearchTree()
{
	Destroy(_root);
}
void Destroy(Node* root)
{
	if(root== nullptr)return ;
	Destroy(root->_left);
	Destroy(root->_right);
	delete root;
}
1
2
3
4
5
6
7
8
9
10
11

源码

#include<iostream>
using namespace std;
namespace key 
{

	template<class K>
	struct BinarySearchTreeNode {
		typedef BinarySearchTreeNode<K> Node;
		Node* _left;
		Node* _right;
		K _key;
		BinarySearchTreeNode(const K& key)
			:_left(nullptr)
			, _right(nullptr)
			, _key(key)
		{}
	};

	template<class K>
	class BinarySearchTree {
		typedef BinarySearchTreeNode<K> Node;
	public:
		bool Erase(const K& key) // 删除指定的节点.
		{
			Node* cur = _root;
			Node* parent = _root;
			while (cur)
			{
				if (cur->_key == key)
				{
					if (cur->_right == nullptr)
					{
						if (cur == _root) {
							_root = _root->_left;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_left;
							}
							else
							{
								parent->_right = cur->_left;
							}
						}
						delete cur;
						return true;
					}
					else if (cur->_left == nullptr)
					{
						if (cur == _root) {
							_root = _root->_right;
						}
						else
						{
							if (cur == parent->_left)
							{
								parent->_left = cur->_right;
							}
							else
							{
								parent->_right = cur->_right;
							}
						}
						delete cur;
						return true;
					}

					// 左右都不为空的时候使用替换法
					else
					{
						Node* rightMinParent = cur; // 这里要用cur进行初始化
						// 右边的最小值
						Node* rightMin = cur->_right;
						while (rightMin->_left)
						{
							rightMinParent = rightMin;
							rightMin = rightMin->_left;
						}
						cur->_key = rightMin->_key;
						if (rightMin == rightMinParent->_left)
							rightMinParent->_left = rightMin->_right;
						else
							rightMinParent->_right = rightMin->_right;
						delete rightMin;
						return true;
					}
				}
				else if (cur->_key > key)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					parent = cur;
					cur = cur->_right;
				}
			}
			return false;
		}
		void Inorder()
		{
			_Inorder(_root);
		}
		bool Insert(const K& k)
		{
			if (_root == nullptr)
			{
				_root = new Node(k);
				return true;
			}
			Node* cur = _root;
			Node* parent = nullptr;
			while (cur)
			{
				if (cur->_key == k)
				{
					return false;
				}
				else if (cur->_key > k)
				{
					parent = cur;
					cur = cur->_left;
				}
				else
				{
					parent = cur;
					cur = cur->_right;
				}
			}
			//保存父节点
			if (k < parent->_key)
			{
				parent->_left = new Node(k);
			}
			else
			{
				parent->_right = new Node(k);
			}
			return true;
		}
		bool Find(const K& k)
		{
			Node* cur = _root;
			while (cur)
			{
				if (cur->_key == k)
				{
					return true;
				}
				else if (cur->_key > k)
				{
					cur = cur->_left;
				}
				else
				{
					cur = cur->_right;
				}
			}
			return false;
		}

		bool FindR(const K& key) //递归找数字
		{
			return _Find(_root, key);
		}
		bool InsertR(const K& key)
		{
			return _Insert(_root, _root, key);
		}
		bool EraseR(const K& key)
		{
			return _Erase(_root, key);
		}

		~BinarySearchTree()
		{
			Destroy(_root);
		}
		// 自动生成默认的构造
		BinarySearchTree() = default;
		// 拷贝构造
		BinarySearchTree(const BinarySearchTree<K>& t)
		{
			this->_root = Copy(t._root);
		}
		// 赋值拷贝
		BinarySearchTree<K>& operator=(const BinarySearchTree<K> t)
		{
			swap(_root, t._root);
			return *this;
		}

	private:
		Node* Copy(const Node* root)
		{
			if (root == nullptr)
				return nullptr;
			Node* newRoot = new Node(root->_key);
			newRoot->_left = Copy(root->_left);
			newRoot->_right = Copy(root->_right);
			return newRoot;
		}
		void Destroy(Node*& root)
		{
			if (root == nullptr)
				return;
			Destroy(root->_left);
			Destroy(root->_right);
			delete root;
		}
		bool _Erase(Node*& root, const K& key)
		{
			if (root == nullptr)
			{
				return false;
			}
			if (root->_key < key)
			{
				return _Erase(root->_right, key);
			}
			else if (root->_key > key)
			{
				return _Erase(root->_left, key);
			}
			else
			{
				Node* del = root;
				if (root->_right == nullptr)
				{
					root = root->_left;
				}
				else if (root->_left == nullptr)
				{
					root = root->_right;
				}
				else
				{
					// 替换法
					Node* rightMin = root->_right;
					while (rightMin->_left)
					{
						rightMin = rightMin->_left;
					}
					swap(rightMin->_key, root->_key);
					// 将当前root位置和rightMin位置的值进行交换,接着在root的右边的树中删除key

					return _Erase(root->_right, key);
				}
				delete del;
				return true;
			}
		}
		// 注意这里的&是不可少的,不然要使用二级指针进行操作了.
		bool _Insert(Node*& root, Node* parent, const K& key)
		{
			if (root == nullptr)
			{
				root = new Node(key);
			}
			if (root->_key > key)
			{
				return _Insert(root->_left, parent, key);
			}
			else if (root->_key < key)
			{
				return _Insert(root->_right, parent, key);
			}
			else if (root->_key == key)
			{
				return false;
			}
		}
		Node* _root = nullptr;
		void _Inorder(Node* root)
		{
			if (root == nullptr)
				return;
			_Inorder(root->_left);
			cout << root->_key << " ";
			_Inorder(root->_right);
		}
		bool _Find(Node* root, const K& key)        
		{
			if (root == nullptr)return false;        
			else if (root->_key == key)return true;        
			else if (root->_key < key)        
			{
				_Find(root->_right, key);        
			}
			else        
			{
				_Find(root->_left, key);        
			}
		}
	};
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196
197
198
199
200
201
202
203
204
205
206
207
208
209
210
211
212
213
214
215
216
217
218
219
220
221
222
223
224
225
226
227
228
229
230
231
232
233
234
235
236
237
238
239
240
241
242
243
244
245
246
247
248
249
250
251
252
253
254
255
256
257
258
259
260
261
262
263
264
265
266
267
268
269
270
271
272
273
274
275
276
277
278
279
280
281
282
283
284
285
286
287
288
289
290
291
292
293
294
295
296
297
298
299

结束

本篇文章就到这里就结束啦,若有不足,请在评论区指正,下期再见,

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/380482