【人工智能】问题规约

基本概念

问题规约法：将某个问题转变为子问题集合，而这些子问题可以直接得到。

组成部分：初始问题描述、一套把初始问题转换为子问题的操作符、一套本原问题描述

与或图如下：

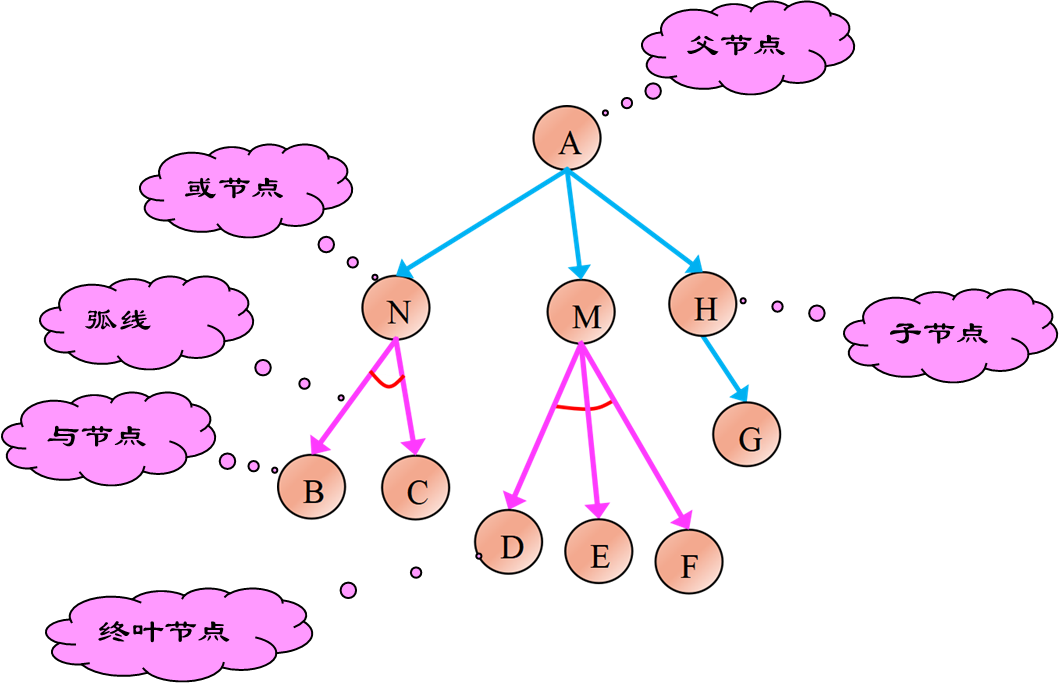
• 如果某条弧线从节点a指向节点b，那么节点a叫做节点b的父辈节点；节点b叫做节点a的后继节点或后裔；
• 或节点，只要解决某个问题就可解决其父辈问题的节点集合；
• 与节点，只有解决所有子问题，才能解决其父辈问题的节点集合；
• 终叶节点，是对应于本原问题的节点
• 可解节点定义：
  • 终叶节点是可解节点（与本原问题对应）
  • 某个非终叶节点含有或后继节点，当其后继节点至少有一个可解时，该非终叶节点为可解节点
  • 某个非终叶节点含有与后继节点，当其后继节点全部可解时，该非终叶节点为可解节点
• 不可解节点：
  • 无后裔的非终叶节点；
  • 含有或后继节点，每个后继节点均不可解
  • 含有与后继节点，至少一个后继节点不可解

与或图搜索

盲目式搜索

与或图的一般搜索、深搜、广搜

1.广搜:

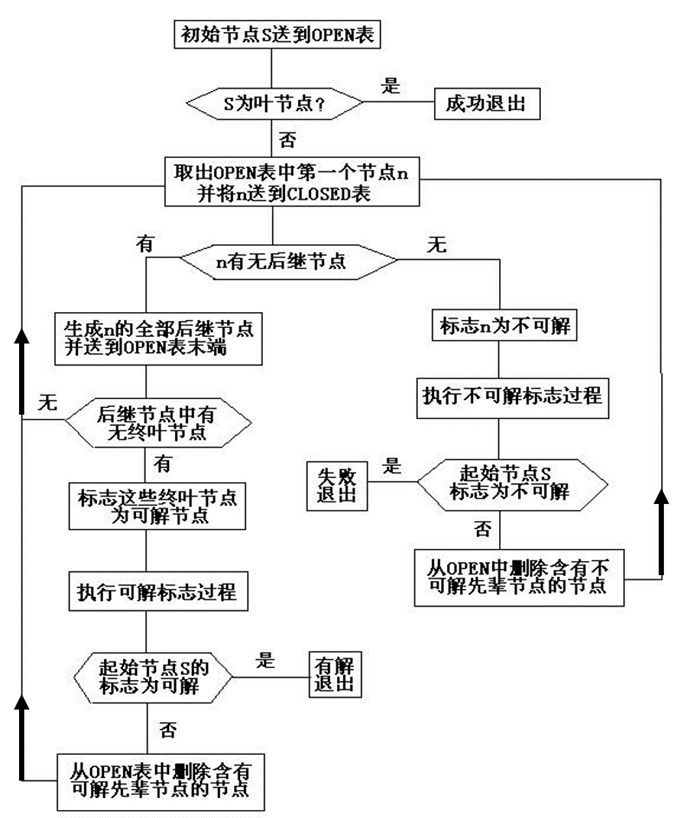
执行可解标志过程：就是对其父节点标识（其某个后继节点是终叶节点），并且向上看此时该节点的父节点能否判断其是否可解。

2.深搜：

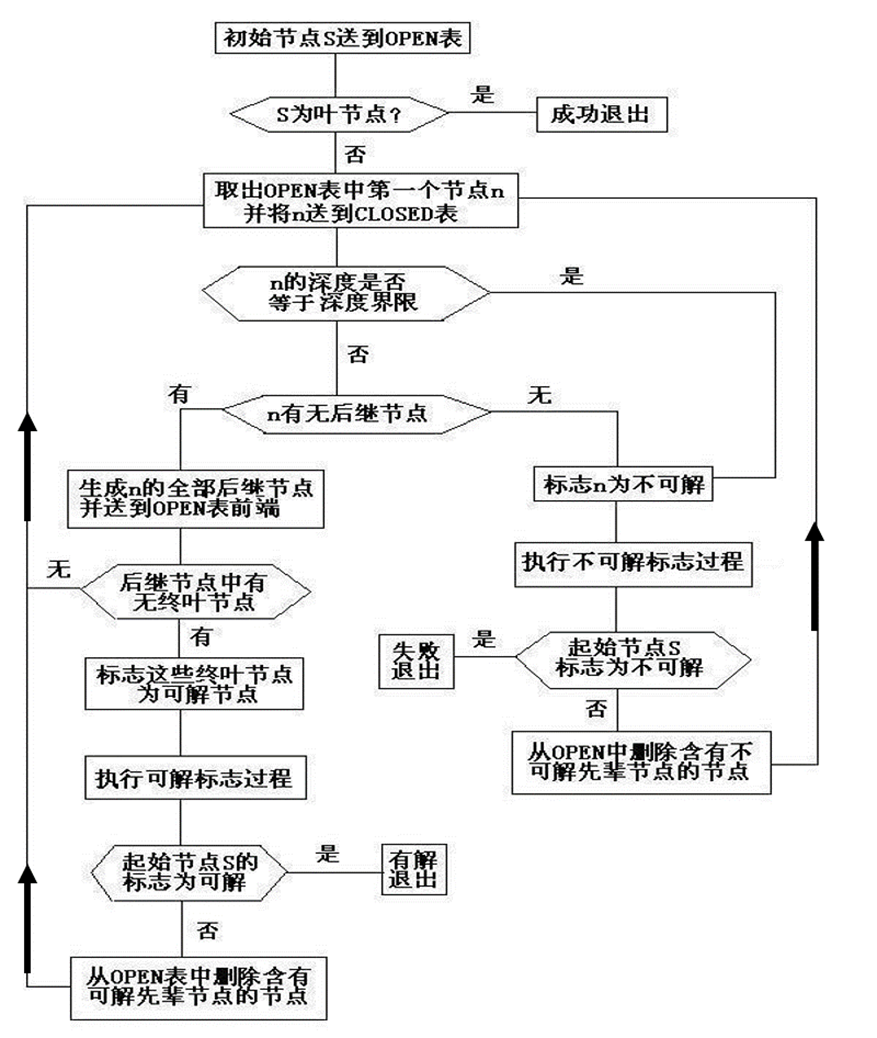
• 要判断从open表取出来的节点的深度。如果等于深度界限，认定它为不可解节点。
• 将扩展出来的节点放到open的前端。

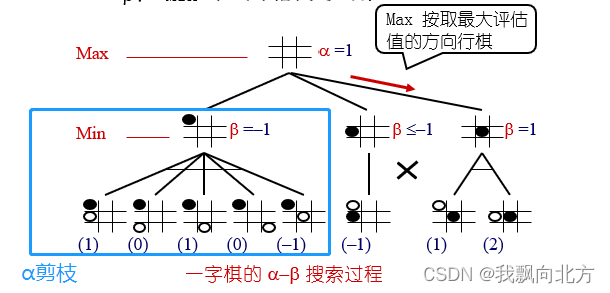
α-β剪枝

基本思想：边生成博弈树边计算评估各节点的倒推值，并且根据评估出的倒推值范围，及时停止扩展那些已无必要再扩展的子节点。

α： Max 节点评估值的下界

β： Min 节点评估值的上界

剪枝规则：

• 对于一个与节点来说，它取当前子节点中的最小倒推值作为它倒推值的上界，称此为β值；(β<= 最小值 )
• 对于一个或节点来说，它取当前子节点中的最大倒推值作为它倒推值的下界，称此为α值.（α >= 最大值）
• α剪枝规则：任何与节点x的β值如果不能升高其父节点的α值，则对节点x以下的分支可停止搜索，并使x的倒推值为β
• β剪枝规则：任何或节点x的α值如果不能降低其父节点的β值，则对节点x以下的分支可停止搜索，并使x的倒推值为α