机器学习快速入门1（机器学习概念与数据预处理）_机器学习入门包括数据预处理这些嘛

1.机器学习介绍

机器学习是一门多领域交叉学科，涉及概率论、统计学、算法理论等多门学科。专门研究计算机怎样模拟或实现人类的学习行为以获得新的知识或者技能。

• 机器学习：可以筛选特征值。例如：垃圾邮件过滤，反欺诈模型。
• 深度学习：不能筛选特征值。例如：图形图像识别、自然语言处理。
• 迁移学习：大厂开源已经训练好模型参数，拿来即用即可。

2 机器学习7大步骤

1.获取数据源
2.清洗与预处理 (耗时)
3.拆分数据集
4.特征工程 (最重要)
5.训练模型 (算力、数据质量)
6.模型调优
7.模型保存与加载

3.数据预处理八大策略

数据预处理是数据分析过程中的重要环节，它直接决定了后期所有数据分析的质量和价值输出。从数据预处理的主要内容看，包括数据清洗、转换、归约、聚合、抽样等8个方向。本章节我们先介绍4种预处理解决方案，剩下4种后续同机器学习案例一同讲解。

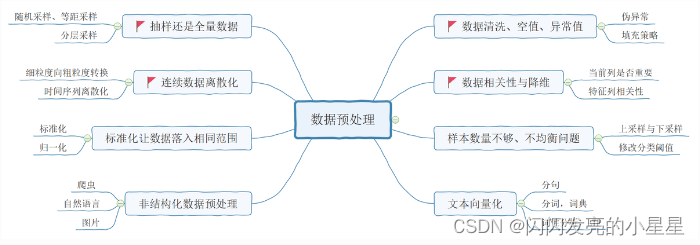
4 缺省值、异常值、重复值处理

在数据清洗过程中，主要处理的是缺失值、异常值、重复值。所谓清洗，是对数据集通过丢弃、填充、替换、去重等操作。达到去除异常、纠正错误、补足缺失的目的。

rand、randn、randint区别¶

import numpy as np
print(np.random.rand(3,4))
# 功能同上,参数传入格式不同
print(np.random.random(size=[3,4]))
# 返回指定范围的整形
print(np.random.randint(low=2, high=10, size=10))
1
2
3
4
5
6

out:

[[0.43886994 0.9828388  0.67412238 0.63591311]
 [0.09833848 0.39956395 0.03163196 0.73770061]
 [0.39373717 0.40119388 0.80123062 0.98700662]]
[[0.41308248 0.94285502 0.23550691 0.43277185]
 [0.335771   0.66001325 0.15082078 0.49722615]
 [0.96614816 0.60807624 0.29640525 0.16006614]]
[3 4 7 4 6 7 2 4 7 3]
1
2
3
4
5
6
7

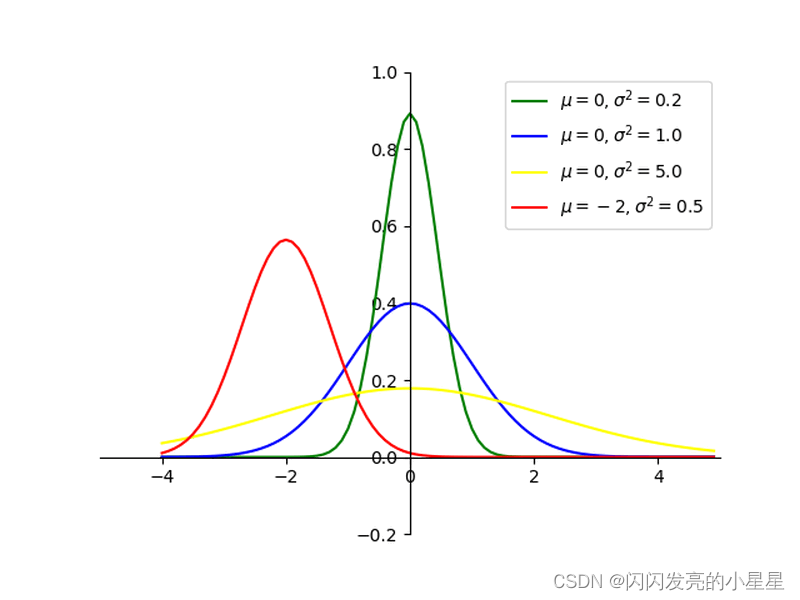
normal与randn¶

import numpy as np
np.random.seed(1)
# 标准正态分布平均数μ=0，对应着整个分布的中心centre
# 标准差σ=1, 此概率分布的标准差(对应于分布的宽度,scale越大越矮胖,scale越小,越瘦高）
value = np.random.normal(loc=0.0, scale=1.0, size=500)
print(np.mean(value),np.std(value))
print(value)
# 绘制可省略
import matplotlib.pyplot as plt
plt.hist(value,bins=100)
plt.show()

np.random.seed(1)
# 从标准正态分布中返回样本
print(np.random.randn(50))
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

缺失值处理

对于缺失值数据，除了丢弃、补全等方法之外还有就是可以忽略。因为有些模型本身对缺失值就比较友好例如：KNN，决策树等。

判断缺失值

import numpy as np
import pandas as pd
df = pd.DataFrame(data=np.random.randn(6,4),columns=list('ABCD'))
df.iloc[0:2,1] = np.nan
df.iloc[4,3] = np.nan
print(df)

# 判断缺失值
print(df.isnull())
print(df.isnull().any())
print(df.isnull().all())
1
2
3
4
5
6
7
8
9
10
11

out:

          A         B         C         D
0 -0.232836       NaN -0.704733  0.096695
1 -1.205989       NaN  1.285456  0.422032
2 -1.641283 -1.849236 -0.758089 -0.408999
3  0.702413  0.332977  0.008190 -0.239250
4 -0.541707 -0.365855 -0.099401       NaN
5 -0.392585 -1.204888  0.738611  1.248117
       A      B      C      D
0  False   True  False  False
1  False   True  False  False
2  False  False  False  False
3  False  False  False  False
4  False  False  False   True
5  False  False  False  False
A    False
B     True
C    False
D     True
dtype: bool
A    False
B    False
C    False
D    False
dtype: bool

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25

• df.isnull().any()会判断哪些列包含缺失值，该列存在缺失值则返回True，反之False
• df. isnull().sum()直接告诉我们每列缺失值的数量
• df[df.isnull().values==True] 只显示存在缺失值的行列，清楚的确定缺失值的位置

删除缺失行

print(df.dropna()) # 直接丢弃有NA的行记录
1

填充缺失值

print(df.fillna(value=0))
print(df.fillna({'B':1.1,'D':0.0}))
print(df.fillna(method='pad'))  # 用前面的值替换缺省值
print(df.fillna(method='backfill',limit=1))  # 用后面的值替换缺省值
print(df.fillna(value=df.mean()))  # 平均值填充
1
2
3
4
5

重复值处理

对于联机分析处理，存在一定的重复数据并不会影响实际分析效果。毕竟数据仅仅是用来做分析的。但是对于联机事务而言。重复数据可能意味重大运营事故。
例如：重复订单会导致重复分拣、出库、送货、退货等反向订单

df = pd.DataFrame(data={'A':['a','b','a','c'],'B':[3,2,3,2]})
print(df)
# 判断重复数据记录
print(df.duplicated())
print(df.drop_duplicates()) #默认保留第一次出现的重复项
print(df.drop_duplicates(['B'],keep='last')) # 根据指定列去删除
1
2
3
4
5
6

out:

   A  B
0  a  3
1  b  2
2  a  3
3  c  2
0    False
1    False
2     True
3    False
dtype: bool
   A  B
0  a  3
1  b  2
3  c  2
   A  B
2  a  3
3  c  2
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

异常值处理

异常数据是数据分布的常态，处于特定分布的区域或者范围之外的数据通常被定义为异常或者”噪音”。但是在有些业务领域异常数据恰恰正常反映了业务运营结果。我们把数据称为伪异常，此类数据通常不处理。
1.公司的A产品正常情况下每日销量100台左右。但是昨天进行网红直播和优惠促销，导致总销量达到1000台。后续几天由于库存不足或者透支了购买力又下降到10台。这恰恰真实反映了业务运营结果。这种数据就称为伪异常
2.网络入侵导致流量异常，日志恰恰记录整个过程
3.贷款申请检测异常，药物变异识别，极端恶劣天气……

import pandas as pd

df = pd.DataFrame(data={'A':[1,120,3,5,2,12,13],'B':[12,17,31,53,22,32,43]})

df_zscore = df.copy()  # 复制一个用来存储Z-score得分的数据框
cols = df.columns  # 获得数据框的列名
# http://blog.sina.com.cn/s/blog_72208a6a0101cdt1.html
# 箱型图
for col in cols:  # 循环读取每列
    df_col = df[col]  # 得到每列的值
    # 计算每列的Z-score得分(是一个数与平均数的差再除以标准差的过程)
    z_score = (df_col - df_col.mean()) / df_col.std()
    # z_score 值就是一个衡量方差的标准 或者说是 单位（unit）
    # 判断Z-score得分是否大于2.2,(此处2.2代表一个经验值)，如果是则是True，否则为False
    df_zscore[col] = z_score.abs() > 2.2
#
print(df_zscore)  # 打印输出
# df_zscore['col1'] == True 的就能丢掉了
df_drop_outlier = df[df_zscore['A'] == False]
print(df_drop_outlier)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

out:

       A      B
0  False  False
1   True  False
2  False  False
3  False  False
4  False  False
5  False  False
6  False  False
    A   B
0   1  12
2   3  31
3   5  53
4   2  22
5  12  32
6  13  43

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

5 抽样VS全量数据

抽样是从整体样本中通过一定的方法选择一部分样本。抽样是数据处理的基本步骤。在科学实验，质量检查，社会调查中普遍采用一种经济有效的研究方法。

为什么需要抽样

1.数据计算资源不足：尤其是在生物，科学工程等领域。
2.数据采集的限制：在社会性调查中必须采用抽样的方法进行研究，因为无法对海量人群做全量调查。
3.时效性要求：抽样本质是局部反应全局，如果进行科学抽样那么时效性会大大增强。
4.抽样可以快速验证概念、算法和模型。

简单随机抽样

import random
import numpy as np

data = np.loadtxt('data/numpy_data_1.txt')
print(data.shape)
# 列表解析式
#print([i for i in range(len(data))])
# 随机抽取2000个样本
print(data[[1,3,5]])
data_sample = data[random.sample([i for i in range(len(data))],2000)]
print(data_sample[:5])
print(data_sample.shape)
1
2
3
4
5
6
7
8
9
10
11
12

out:

(10000, 5)
[[-4.03307362  8.58624006  3.897472    1.26982588 -9.01924785]
 [-3.02463329  8.41403228  5.58731866  2.26420369 -7.51518693]
 [-2.11984871  7.74916701  5.7318711   4.75148273 -5.68598747]]
[[ -5.57465702  -7.20583786   6.48864731   4.57379445   4.57894367]
 [ -8.25472343   9.35037535   6.22548077  -6.52089237  -6.29023882]
 [ -1.1558427   10.69331093   2.29579994   2.83903124  -5.81093984]
 [ -8.36576509 -10.30443934   8.08582738   0.58637358   3.89069806]
 [-10.23501637   8.94114407   4.94090456  -5.28925329  -5.9268967 ]]
(2000, 5)
1
2
3
4
5
6
7
8
9
10

等距抽样

先计算抽样的间距，然后根据间距抽取个体。也适合均衡分布,无明显周期的场景，对于不均衡，增减趋势的数据会出现偏差

import numpy as np

# 等距抽样
data = np.loadtxt('../data/numpy_data_1.txt')
sample_count = 2000
record_count = data.shape[0]
width = record_count / sample_count  # 计算抽样间距
result_sample = []  # list 而非 ndarray
i = 0
# 当样本量小于指定抽样数据并且索引在有效范围内时
while len(result_sample) < sample_count and i * width < record_count:
    result_sample.append(data[int(i * width)]) # 新增样本
    i +=i
result_sample = np.array(result_sample)
print(result_sample[:5])
print(result_sample.shape)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16

分层抽样

将所有样本按照某种特征划分为几个类别(时间序列、月份….)。然后从每个类别中在使用随机或者等距抽样方式选择个体样本，一般适合分类数据。

import numpy as np
# 分层抽样
data = np.loadtxt('  data/numpy_data_2.txt')
each_sample_count = 100   # 定义每个分层的抽样数量
label_y = np.unique(data[:,-1])  # 获取分层的值域
print(label_y)
sample_data = []
sample_dict = {}
for y in label_y:
    sample_list = []    # 用于存储临时分层数据
    for row in data:
        if row[-1] == y:
            sample_list.append(row)   # 将数据加入分层数据中
    # 对当前类别数据集进行随机采样
    each_sample_data = random.sample(sample_list,each_sample_count)
    # 将抽样数据追加到总体样本集
    sample_data.extend(each_sample_data)
    # 添加样本统计结果
    sample_dict[y] = len(each_sample_data)
print(sample_dict)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

• 有label的数据，分别对各个label的数据进行采样
• 如果没有label，考虑使用聚类等方法打label

整群抽样

先将所有样本分为几个小群体，然后随机抽取小群体来代表总体。此方式会有一定误差，比较适合小群体特征差异比较小的数据。

# 分群代码如下，每个群体的采用参考上面代码
data = np.loadtxt('../data/numpy_data_2.txt')
label_y = np.unique(data[:,-1])
print(label_y)
sample_label = random.sample(set(label_y),2)
print(sample_label)
1
2
3
4
5
6

6 相关性与特征共线

所谓共线问题是指输入的自变量之间存在较高的线性相关度。共线问题会导致回归模型的稳定性和准确性下降。另外过多的维度参与计算也会浪费计算资源和时间。常见的共线维度变量如下：
1.订单和销售额
2.促销费用和销售额
3.学历与学位

如何检测共线问题

1.容忍度
2.方差膨胀因子 (与容忍度互为倒数)
3.主成分分析
4.相关性
注意事项：完全解决共线问题是不可能的，因为任何事物之间都存在一定的联系，在解决共线问题的相关性活动中。我们只是解决其中严重共线问题，而非全部共线问题。

协方差

标准差和方差一般是用来描述一维数据的，而在概率论统计学中，协方差用于衡量两组随机变量的相关性
1.方差永远为正，而协方差可正可负
2.协方差不仅度量两随机变量离散程度，还反映相关状况 (协方差为正，表示正相关，为负表示负相关)
3.Cov(X,Y)=E(XY)-E(X)E(Y)

x=[1.1, 1.9, 3]
y=[5.0, 10.4, 14.6]
ex = (1.1+1.9+3)/3
ey = (5.0+10.4+14.6)/3
exy=(1.1 * 5.0+1.9 * 10.4 + 3 * 14.6)/3
# 计算协方差公式
cov_x_y= exy - ex * ey  # 23.02-2×10=3.02
print(ex,ey,exy,cov_x_y)
1
2
3
4
5
6
7
8

皮尔逊相关系数

皮尔逊相关系数r是用来描述两个变量间线性相关强弱程度的统计量，R的绝对值越大表明相关性越强。r取值范围为【-1,1】，为正代表两个变量存在正相关，为负代表两个变量存在负相关。其计算公式如下:其中D(X)和D(Y)为变量X和Y的方差，COV(X,Y)为变量X和Y的协方差。

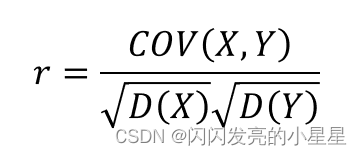
皮尔逊相关系数的数学原理：
1.只需给它两个数组(X,Y)，它就能返回两个数值(r,P):
相关系数r值在【-1，1】之间，为正数则表示正相关，负数则表示负相关，绝对值越大相关性越高。
2.P值是显著性，与皮尔逊相关显著性检验有关，P<0.05时表示相关显著，即指变量X和Y之间真的存在相关性，而不是因为偶然因素引起的。(样本大于500 P值才有意义)
3.相关系数是用协方差除以两个变量的标准差得到的。

import numpy as np

x=[1.1, 1.9, 3]
y=[5.0, 10.4, 14.6]
ex = (1.1+1.9+3)/3
ey = (5.0+10.4+14.6)/3
exy= (1.1 * 5.0 + 1.9 * 10.4 + 3 * 14.6) / 3
# 计算协方差公式
cov_x_y= exy - ex * ey  # 23.02-2×10=3.02
print(ex,ey,exy,cov_x_y)
# 计算皮尔逊系数
# r(X,Y)=Cov(X,Y)/((std(x) * std(y)) = 3.02 /(0.77×3.93) = 0.9979
print('std',np.std(x),np.sqrt(np.average((x - np.mean(x))**2)))
print('std',np.std(y))
print(cov_x_y / (np.std(x) * np.std(y)))
from scipy.stats import pearsonr
# 采用官方皮尔逊公式
corr = pearsonr(x,y)
print(corr)
print(np.corrcoef(X,Y)) # 相关性分析
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20

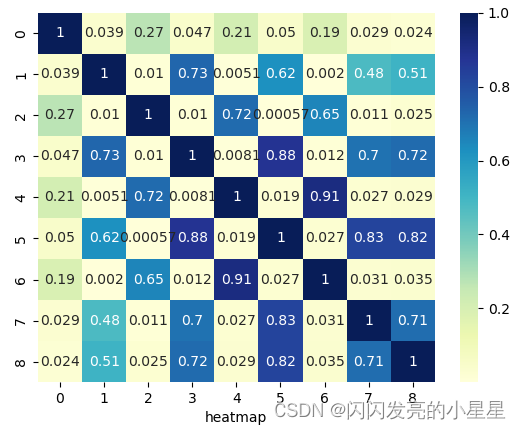
相关性实现与可视化

import numpy as np

data = np.loadtxt('../data/numpy_data_3.txt',delimiter='\t')
x = data[:,:-1]
# 变量相关性矩阵
matrix = np.corrcoef(x,rowvar=False) # 相关性分析
print(matrix.round(2))

import pandas as pd
df_ads = pd.DataFrame(x)
print(df_ads.corr().round(2))

# 对所有的标签和特征两两显示其相关性的热力图(heatmap)
# annot = True 在每个方格显示数值
import matplotlib.pyplot as plt
import seaborn as sns
sns.heatmap(np.abs(matrix), cmap="YlGnBu", annot = True,)
plt.xlabel('heatmap')
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

离散化实现数据逻辑分层

离散化本质上把无限的空间中有限的个体映射到有限的空间中。数据离散化操作大多是针对连续数据。处理之后的数据值域分布将从连续数据变为离散数据。
1.节省计算资源，提高计算效率
2.算法模型需要。虽然很多模型支持连续数据输入，但是数据在训练之前还是先把连续数据转化为离散数据。离散化是必要步骤。
3.弱化异常数据带来的负面效果
4.业务应用的需要

离散化场景需求¶

1.工资、成绩数据分类
2.时间序列数据
3.用户画像与推荐系统需要
4.评论留言的离散化

时间数据离散化

时间数据的离散化主要用于细粒度向粗粒度转换。离散化之后将分散的时间特征转换为更高层次的时间特征。

import pandas as pd

df = pd.read_csv("../data/numpy_data_4.txt",sep='\t',names=['id','amount','income','datetime','age'])
print(df.head(5))
# 日期序列化，把时间转化为周为基本单位
df['datetime'] = list(map(pd.to_datetime,df['datetime']))
df['datetime'] = [i.weekday() for i in df['datetime']]
print(df.head(5))
1
2
3
4
5
6
7
8

out:

      id  amount  income             datetime    age
0  15093    1390   10.40  2017-04-30 19:24:13   0-10
1  15062    4024    4.68  2017-04-27 22:44:59  70-80
2  15028    6359    3.84  2017-04-27 10:07:55  40-50
3  15012    7759    3.70  2017-04-04 07:28:18  30-40
4  15021     331    4.25  2017-04-08 11:14:00  70-80
      id  amount  income  datetime    age
0  15093    1390   10.40         6   0-10
1  15062    4024    4.68         3  70-80
2  15028    6359    3.84         3  40-50
3  15012    7759    3.70         1  30-40
4  15021     331    4.25         5  70-80

1
2
3
4
5
6
7
8
9
10
11
12
13

聚类实现离散化

聚类算法本质上属于无监督算法，主要是对样本进行只能分类(离散化)。如果样本只有一列特征那么就是对列进行离散化操作。

from sklearn.cluster import KMeans
# 采用聚类实现离散化
data = df['amount']
data_reshape = data.values.reshape(data.shape[0],1)
model_kmeans = KMeans(n_clusters=4,random_state=0)
kmeans_result = model_kmeans.fit_predict(data_reshape)
df['amount2'] = kmeans_result
print(df)
1
2
3
4
5
6
7
8

采用map 实现离散化

def cluValue(val):
    if val > 7500:
        return 4
    elif val > 5000:
        return 3
    elif val > 2500:
        return 2
    else:
        return 1

print(df.describe())
df['amount3'] = df['amount'].map(cluValue)
print(df)
1
2
3
4
5
6
7
8
9
10
11
12
13