〔Part2〕YOLOv5：原理+源码分析--训练技巧（warm-up、AutoAnchor、hyper、GA、AMP、autocast、gradscaler、dist、DDP、node）_yolov5 warmup

5. YOLOv5 训练技巧

5.1 warm-up

在 YOLOv5 中，warm-up（预热）是指在训练初始阶段使用较小的学习率，然后逐渐增加学习率，以帮助模型更好地适应数据集。这个过程有助于避免在初始阶段出现梯度爆炸或不稳定的情况，使模型更容易收敛。

YOLOv5 中的 warm-up 主要体现在学习率的调整上。具体而言，YOLOv5 使用线性 warm-up 策略，即在初始训练阶段，学习率从一个较小的初始值线性增加到设定的初始学习率。这有助于减缓模型的参数更新速度，防止在初始时出现过大的权重更新，从而提高训练的稳定性。

在 YOLOv5 的实现中，warm-up 阶段通常持续一定的迭代次数，这个次数是在训练开始时设定的。一旦 warm-up 阶段结束，模型将以设定的初始学习率进行正常的训练。

Warm-up 的主要优势在于可以在模型开始学习任务时更好地控制学习的速度，从而有助于模型更快地适应数据分布。这在处理复杂的目标检测任务中尤为重要，因为这些任务通常具有大量的样本和复杂的背景。

我们看一下相关的源码（train.py）：

nb = len(train_loader)  # number of batches | 一个epoch拥有的batch数量
nw = max(round(hyp["warmup_epochs"] * nb), 100)  # number of warmup | 热身的总迭代次数

pbar = enumerate(train_loader)  # 遍历train_loader

# 记录日志
LOGGER.info(("\n" + "%11s" * 7) % ("Epoch", "GPU_mem", "box_loss", "obj_loss", "cls_loss", "Instances", "Size"))

# 如果在主线程中，那么给enumberate加上tqdm进度条
if RANK in {-1, 0}:
    pbar = tqdm(pbar, total=nb, bar_format=TQDM_BAR_FORMAT)  # progress bar

# 开始遍历train_loader
for i, (imgs, targets, paths, _) in pbar:  # batch 
    # imgs: 一个batch的图片
    # targets: 一个batch的标签
    # paths: 一个batch的路径
    callbacks.run("on_train_batch_start")  # 记录此时正在干什么

    # 计算当前的迭代次数
    ni = i + nb * epoch  # number integrated batches (since train start)
    imgs = imgs.to(device, non_blocking=True).float() / 255  # uint8 to float32, 0-255 to 0.0-1.0

    # Warmup
    if ni <= nw:  # 如果当前的迭代次数小于需要热身的迭代次数，则开始热身
        xi = [0, nw]  # x interp

        # accumulate变量的作用是动态地控制累积的 Batch 数，以便在训练开始时逐渐增加累积的 Batch 数，
        # 从而实现从较小的累积 Batch 数到较大的累积 Batch 数的平滑过渡
        # 这有助于模型在训练初期稳定地学习
        accumulate = max(1, np.interp(ni, xi, [1, nbs / batch_size]).round())
        for j, x in enumerate(optimizer.param_groups):
            # bias lr falls from 0.1 to lr0, all other lrs rise from 0.0 to lr0
            x["lr"] = np.interp(ni, xi, [hyp["warmup_bias_lr"] if j == 0 else 0.0, x["initial_lr"] * lf(epoch)])
            if "momentum" in x:
                x["momentum"] = np.interp(ni, xi, [hyp["warmup_momentum"], hyp["momentum"]])
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36

在 How suspend image mixing #931 中有作者关于 warm-up 的说明：

warmup 慢慢地将训练参数从它们的初始（更稳定）值调整到它们的默认训练值。例如，通常会在最初的几个 Epoch 内将学习率从 0 调整到某个初始值，以避免早期训练的不稳定、nan 等问题。

热身效果可以在 Tensorboard 的学习率曲线图中观察到，这些曲线自从最近的提交以来已经被自动跟踪。下面的例子显示了在自定义数据集上大约 30 个 Epoch 的热身，每个参数组有一个曲线图。最后一个曲线图展示了不同的热身策略（即不同的超参数设置）。

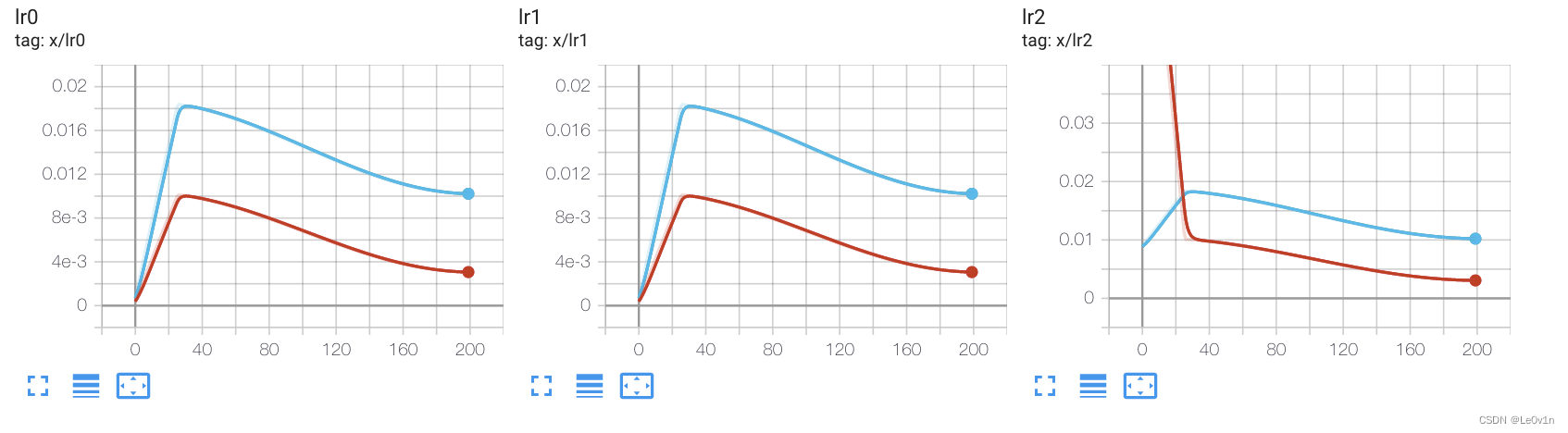
5.1.1 np.interp 语法

numpy.interp(x, xp, fp, left=None, right=None, period=None) 是 NumPy 中的一个函数，用于线性插值。线性插值是一种估算在两个已知值之间的未知值的方法，假设这些值之间的变化是线性的。

其中：

• x: 需要进行插值的一维数组。
• xp: 已知数据点的 x 坐标（一维数组）-> x points。
• fp: 已知数据点的 y 坐标（一维数组）-> function points。
• left: 当 x 小于 xp 的最小值时，返回的默认值，默认为 fp[0]。
• right: 当 x 大于 xp 的最大值时，返回的默认值，默认为 fp[-1]。
• period: 如果提供了 period，表示 xp 是周期性的，此时插值会考虑周期性。period 是周期的长度。

示例：

import numpy as np
import matplotlib.pyplot as plt

# 已知数据点
x_known = np.array([1, 2, 3, 4, 5])
y_known = np.array([3, 5, 7, 9, 11])

# 待插值的数据点
x_unknown = [0.0, 1.5, 3.0, 4.5, 6.0]

# 使用np.interp进行插值
y_unknown = np.interp(x_unknown, x_known, y_known)
print(f"{y_unknown = }")  # [3, 4, 7, 10, 11]

# 绘制图形
plt.figure(figsize=(10, 6), dpi=200)
plt.plot(x_known, y_known, 'o', label='Known points', color='green')  # 已知数据点
plt.plot(x_unknown, y_unknown, 'o', label='Unknown points', color='red')  # 插值结果
plt.xlabel('x')
plt.ylabel('y')
plt.title(r'Example for $np.interp()$')
plt.legend()
plt.grid(True)
plt.savefig('Example4np.interp.jpg')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

看不懂没关系，我们作图看一下：

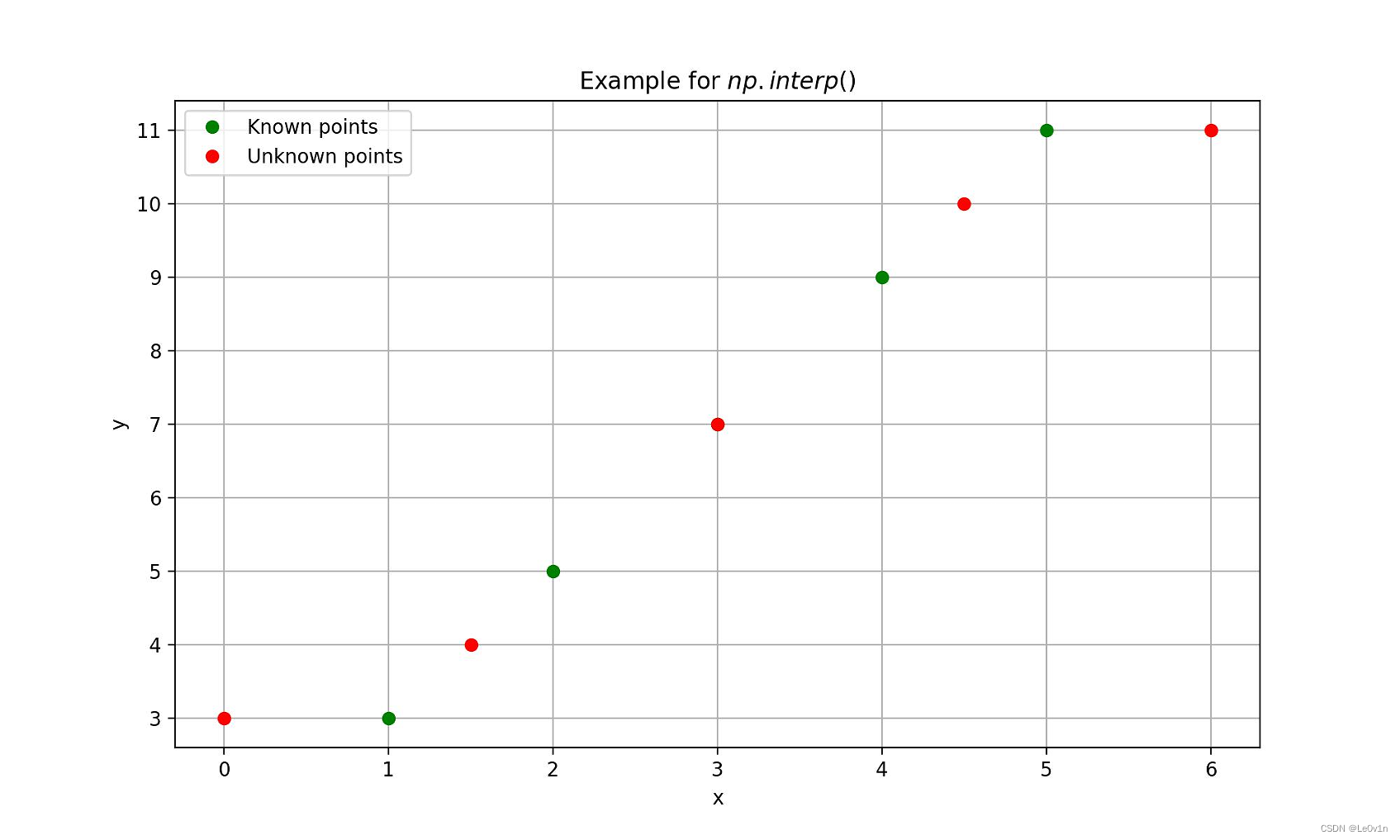
外推规则如下：

• 如果 x 的值小于 xp 的最小值，则 np.interp 返回与 xp 最小值对应的 fp 值。
• 如果 x 的值大于 xp 的最大值，则 np.interp 返回与 xp 最大值对应的 fp 值。

分析如下：

• x[0] = 0.0, 它小于 xp 的最小值1，所以外推，此时 x[0] 对应的 y[0] = fp[0] -> 3
• x[1] = 1.5, 它在 xp 的 [1, 2] 之间，所以对应的 y[1] 应该为 y[0] = (fp[1] + f[2]) / 2 --> (3 + 5) / 2 = 4
• x[2] = 3.0 == xp[2], 所以对应的 y[2] == fp[2] --> 7
• x[3] = 4.5 ∈ [4, 5], y[3] == (fp[4] + fp[5]) / 2 --> (9 + 11) / 2 --> 10
• x[4] = 6.0，它大于 xp 的最大值，所以外推，此致 x[4] 对应的 y[4] == fp[5] --> 11

⚠️ x 和 y 取的是索引，而 xp 和 fp 这里不是取索引，而是取值

5.2 Cosine Annealing Warm Restart

• 论文地址：SGDR: Stochastic Gradient Descent with Warm Restarts
• 翻译：Cosine Annealing Warm Restart论文讲解

Cosine Annealing Warm Restart 是一种学习率调度策略，它是基于余弦退火周期性调整学习率的算法。这种策略在学习率调整上引入了周期性的“重启”，使得模型在训练过程中能够周期性地跳出局部最小值，从而有助于提高模型的泛化能力和性能。

具体来说，Cosine Annealing Warm Restart 策略包括以下几个关键组成部分：

1. 余弦退火周期：在每个周期内，学习率按照余弦函数的变化规律进行调整。余弦函数从最大值开始，逐渐减小到最小值，因此学习率也会从初始值开始，先减小到一个低点，然后再增加回到初始值。
2. 周期性重启：在每个周期结束时，学习率会被重新设置回初始值，并重新开始一个新的周期。这种重启有助于模型跳出当前的优化路径，探索新的参数空间。
3. 周期长度调整：随着训练的进行，周期长度（即退火周期）和最小学习率可以逐渐调整。通常，每个周期的长度会逐渐减小，而最小学习率会逐渐增加，这样可以让模型在训练后期更加细致地搜索最优解。
4. 学习率范围：在每个周期内，学习率的变化范围是从最大值到最小值，这两个值都可以根据实际情况进行调整。

Cosine Annealing Warm Restart 策略的优势在于它通过周期性重启和调整周期长度，使得模型能够在训练过程中不断探索新的参数空间，从而有可能找到更好的局部最小值或全局最小值。这种策略特别适合于那些容易陷入局部最小值的复杂模型训练，可以提高模型的最终性能和泛化能力。

在论文 Bag of Tricks for Image Classification with Convolutional Neural Networks 中有介绍到余弦退火和阶段两种学习率在 ImageNet 数据集上的表现（模型为 ResNet-50）：

图 3：带有热身阶段的学习率计划的可视化。顶部：Batch size=1024 下的余弦和阶跃调度。底部：两种调度下的Top-1验证准确率曲线。

---

余弦退火热重启的调用如下：

import torch.optim as optim


model = ...
optimizer = optim.Adam(model.parameters(), lr=0.001)

# 使用CosineAnnealingWarmRestarts调度器
# T_0是初始周期的大小，T_mult每个周期结束后周期大小乘以的倍数
scheduler = optim.lr_scheduler.CosineAnnealingWarmRestarts(optimizer, T_0=10, T_mult=2)

for epoch in range(num_epochs):
    # 训练模型的代码
    train(...)
    # 在每个epoch后更新学习率
    scheduler.step(epoch)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15

在上面的代码中，T_0 参数代表初始周期的大小，即在第一次余弦退火周期中，学习率将按照余弦调度进行调整的 Epoch 数。T_mult 参数指定了每个周期结束后周期大小将乘以的倍数。scheduler.step(epoch) 应该在每次更新参数之后、每个epoch结束时调用。
请根据我们的具体需求调整 T_0 和 T_mult 的值，以及 num_epochs，即我们的训练周期总数。

5.3 YOLOv5-v7.0 使用的 Scheduler

# Scheduler
if opt.cos_lr:  # 如果使用cosine学习率
    lf = one_cycle(1, hyp["lrf"], epochs)  # cosine 1->hyp['lrf']
else:
    lf = lambda x: (1 - x / epochs) * (1.0 - hyp["lrf"]) + hyp["lrf"]  # linear
scheduler = lr_scheduler.LambdaLR(optimizer, lr_lambda=lf)  # plot_lr_scheduler(optimizer, scheduler, epochs)
1
2
3
4
5
6

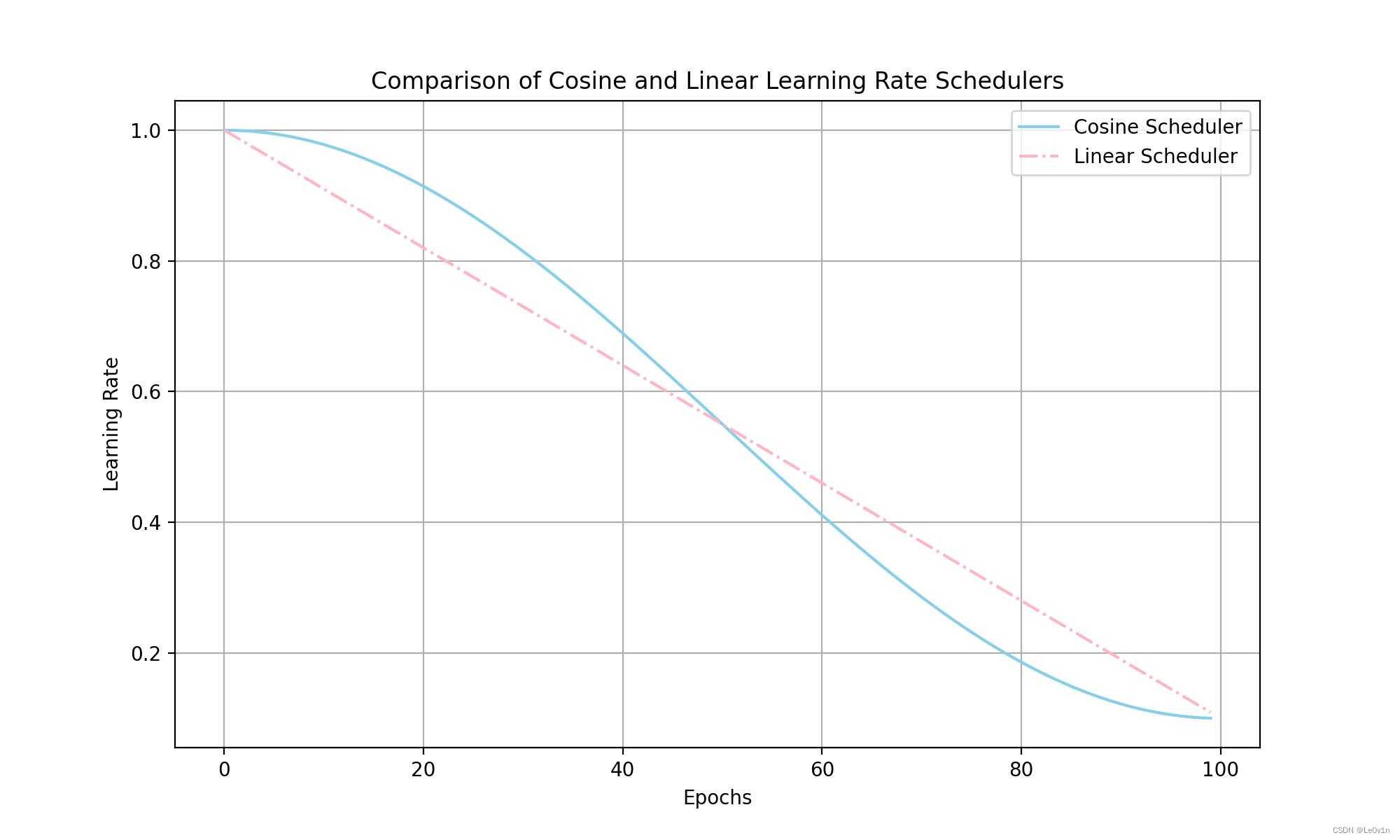
我们画图看一下二者的区别：

import matplotlib.pyplot as plt
import math


def one_cycle(y1=0.0, y2=1.0, steps=100):
    # lambda function for sinusoidal ramp from y1 to y2 https://arxiv.org/pdf/1812.01187.pdf
    return lambda x: ((1 - math.cos(x * math.pi / steps)) / 2) * (y2 - y1) + y1


# 设定训练的总epoch数
epochs = 100

# YOLOv5中的超参数
hyp = {
    "lr0": 0.01,  # 初始学习率
    "lrf": 0.1  # final OneCycleLR learning rate (lr0 * lrf)
}

# 创建一个numpy数组，表示epoch数
epoch_lst = range(epochs)

# Cosine调度器的学习率变化
lf_cos = one_cycle(1, hyp["lrf"], epochs)
lr_cos = [lf_cos(epoch) for epoch in epoch_lst]

# Linear调度器的学习率变化
lf_lin = lambda x: (1 - x / epochs) * (1.0 - hyp["lrf"]) + hyp["lrf"]
lr_lin = [lf_lin(epoch) for epoch in epoch_lst]

# 绘制学习率变化曲线
plt.figure(figsize=(10, 6), dpi=200)

plt.plot(epoch_lst, lr_cos, '-', label='Cosine Scheduler', color='skyblue')
plt.plot(epoch_lst, lr_lin, '-.', label='Linear Scheduler', color='lightpink')

plt.xlabel('Epochs')
plt.ylabel('Learning Rate')
plt.title('Comparison of Cosine and Linear Learning Rate Schedulers')

plt.legend()
plt.grid(True)
plt.savefig('Le0v1n/results/Comparison-of-Cosine-and-Linear-Learning-Rate-Schedulers.jpg')
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42

5.3 AutoAnchor

5.3.1 目的

AutoAnchor 是 YOLOv5 中的一个功能，用于自动调整 Anchor（anchor boxes）的大小以更好地适应训练数据集中的对象形状。

Anchor 是在对象检测任务中使用的一种技术，它们代表了不同大小和宽高比的预定义边界框，用于预测真实对象的位置和大小。

在 YOLOv5 中，AutoAnchor 的主要目的是优化 Anchor 的大小，以便在训练期间提高检测精度和效率。这个功能在训练过程开始时执行，根据训练数据集中的边界框计算最佳 Anchor 配置。通过这种方式，YOLOv5 可以自动适应新的数据集，而无需手动调整 Anchor。

5.3.2 AutoAnchor 的步骤

1. 分析数据集：分析数据集中的边界框，了解对象的大小和形状分布。
2. Anchor聚类：使用聚类算法（如 K-means）对边界框进行聚类，以确定最佳的 Anchor 数量和大小。
3. 更新配置：根据聚类结果更新 Anchor 配置，以便在训练期间使用这些新 Anchor。
4. 重新训练：使用新的 Anchor 配置重新开始训练过程。

5.3.3 作用

AutoAnchor 的优势在于它能够为特定的数据集定制 Anchor，这有助于提高检测精度，尤其是在处理具有不同对象大小和形状的多样化数据集时。通过自动调整 Anchor，YOLOv5 可以更有效地利用计算资源，减少对超参数的手动调整需求，从而简化了模型训练过程。

5.3.4 源码

首先需要先计算当前的 Anchor 与数据集的适应程度。

@TryExcept(f"{PREFIX}ERROR")
def check_anchors(dataset, model, thr=4.0, imgsz=640):
    # 函数作用：检查anchor是否适合数据，如有必要，则重新计算anchor

    # 从模型中获取检测层（Detect()）
    m = model.module.model[-1] if hasattr(model, "module") else model.model[-1]
    
    # 计算输入图片的尺寸相对于最大尺寸的比例
    shapes = imgsz * dataset.shapes / dataset.shapes.max(1, keepdims=True)

    # 生成一个随机的比例因子，用于扩大或缩小图片尺寸
    scale = np.random.uniform(0.9, 1.1, size=(shapes.shape[0], 1))

    # 计算所有图片的宽高（wh）
    wh = torch.tensor(np.concatenate([l[:, 3:5] * s for s, l in zip(shapes * scale, dataset.labels)]))

    def metric(k):  # 计算度量值
        # 计算每个anchor与gt boxes的宽高比
        r = wh[:, None] / k[None]

        # 计算最小比率和最大比率
        x = torch.min(r, 1 / r).min(2)[0]

        # 找到最大比率的anchor
        best = x.max(1)[0]

        # 计算超过阈值（thr）的anchor数量占比
        aat = (x > 1 / thr).float().sum(1).mean()

        # 计算BPR（best possible recall）
        bpr = (best > 1 / thr).float().mean()

        return bpr, aat

    # 获取模型的步长（stride）
    stride = m.stride.to(m.anchors.device).view(-1, 1, 1)

    # 计算当前的anchor
    anchors = m.anchors.clone() * stride
    
    # 计算当前anchor与gt boxes的比值，并找到最佳比值和超过阈值的anchor占比
    bpr, aat = metric(anchors.cpu().view(-1, 2))
    s = f"\n{PREFIX}{aat:.2f} anchors/target, {bpr:.3f} Best Possible Recall (BPR). "
    
    # 如果最佳比值召回率大于0.98，说明当前anchor适合数据集
    if bpr > 0.98:
        LOGGER.info(f"{s}Current anchors are a good fit to dataset ✅")
    else:  # 说明anchor不适合数据集，需要尝试改进
        LOGGER.info(f"{s}Anchors are a poor fit to dataset ⚠️, attempting to improve...")

        # 计算anchor数量
        na = m.anchors.numel() // 2

        # 使用k-means聚类算法重新计算anchor
        anchors = kmean_anchors(dataset, n=na, img_size=imgsz, thr=thr, gen=1000, verbose=False)

        # 计算新anchor的最佳比值召回率
        new_bpr = metric(anchors)[0]

        # 如果新anchor的召回率比原来的高，则替换anchor
        if new_bpr > bpr:
            anchors = torch.tensor(anchors, device=m.anchors.device).type_as(m.anchors)
            m.anchors[:] = anchors.clone().view_as(m.anchors)

            # 检查anchor顺序是否正确（必须在像素空间，不能在网格空间）
            check_anchor_order(m)
            m.anchors /= stride
            s = f"{PREFIX}Done
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68

5.4 Hyper-parameter Evolution 超参数进化

超参数进化（Hyperparameter Evolution）是一种模型优化技术，它涉及在训练过程中动态地调整模型的超参数（hyperparameters），以找到在特定数据集上性能最佳的参数设置。这些超参数是模型设计中的高级设置，它们控制模型的学习过程，但不直接作为模型输入的一部分。常见的超参数包括学习率、批量大小、迭代次数、正则化参数、Anchor 大小等。

超参数进化的目标是减少超参数调整的试错过程，提高模型训练的效率。传统的超参数调整方法通常需要手动调整超参数或使用网格搜索（Grid Search）等方法进行大量的实验来找到最佳设置。这些方法既耗时又可能无法找到最优解。

在 《超参数演变》 这一官方文档中对其进行了介绍：

超参数演化是一种使用遗传算法（GA）进行优化的超参数优化方法。

ML 中的超参数控制着训练的各个方面，而为超参数寻找最佳值是一项挑战。网格搜索等传统方法很快就会变得难以处理，原因在于：1）搜索空间维度高；2）维度之间的相关性未知；3）评估每个点的适配性成本高昂，因此 GA 是超参数搜索的合适候选方法。

GA 的流程如下：

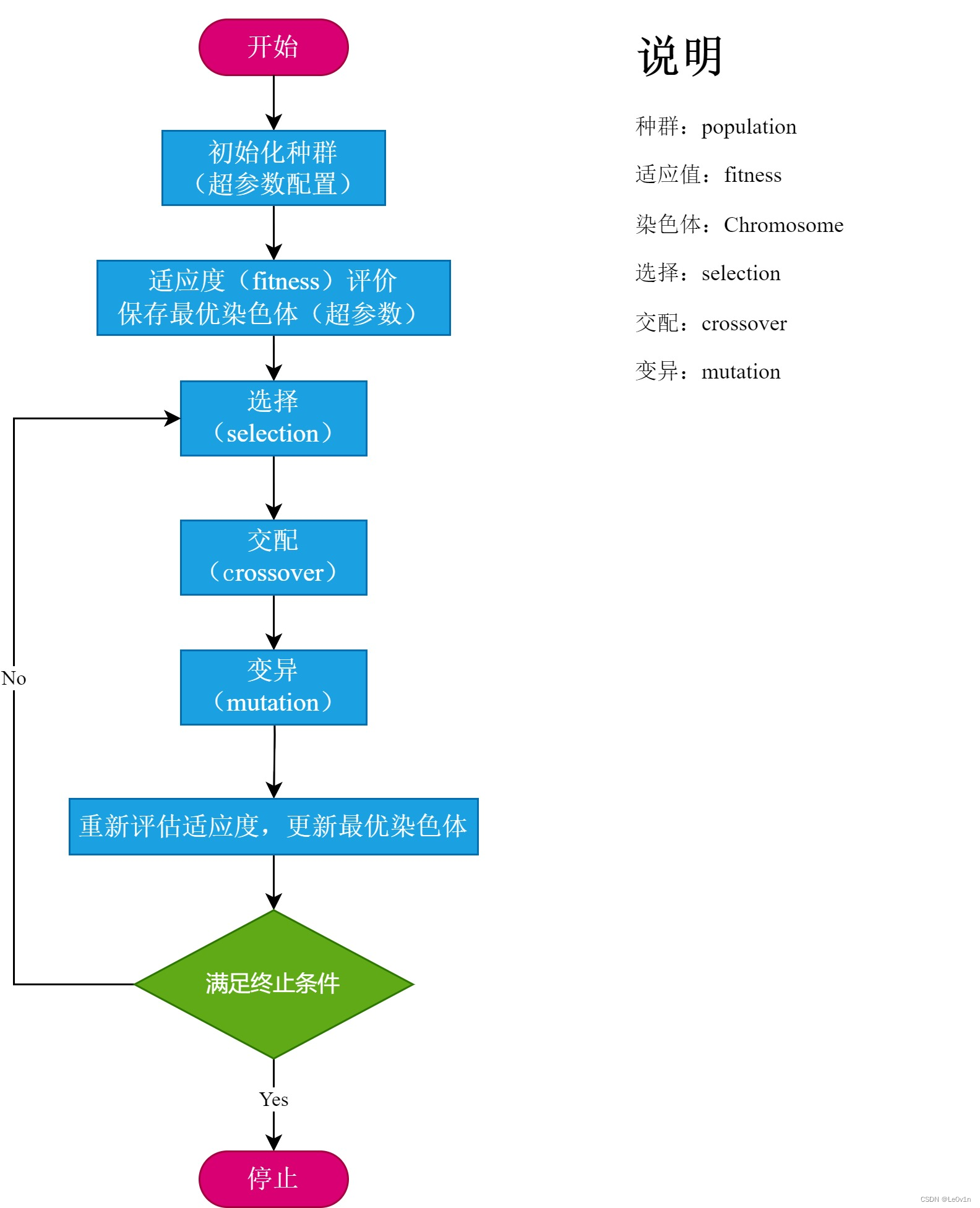
我们看一下官方的介绍：

5.4.1 初始化超参数

YOLOv5 有大约 30 个超参数，用于不同的训练设置。这些参数在 *.yaml 文件中的 /data/hyps 目录。更好的初始猜测将产生更好的最终结果，因此在演化之前正确初始化这些值非常重要。如果有疑问，只需使用默认值即可，这些值已针对 YOLOv5 COCO 从头开始的训练进行了优化。

# YOLOv5 
声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/weixin_40725706/article/detail/307682