二叉树链式结构的实现及简单操作（画图超详细解释）_二叉树的链表画图

前置说明

由于我们要对二叉树进行操作，我们就得现有一个二叉树，而二叉树的构建又比较复杂，为此我们先来手动创建一颗二叉树！
比如现在我们就建立如图的二叉树：

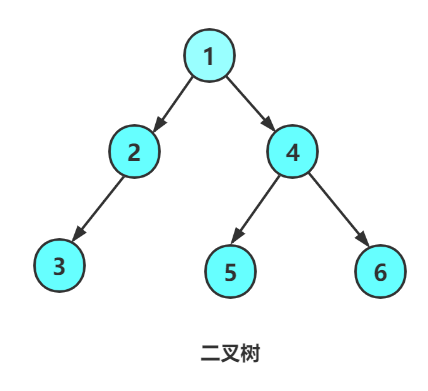
typedef int BTDataType;
typedef struct BTNode
{
	struct BTNode* left;
	struct BTNode* right;
	BTDateType val;
}BTNode;
// 通过前序遍历的数组"ABD##E#H##CF##G##"构建二叉树
BTNode* BuyBTNode(BTDataType x)
{
	BTNode* ret = (BTNode*)malloc(sizeof(BTNode));
	if (!ret)
		exit(EXIT_FAILURE);
	ret->val = x;
	ret->left = NULL;
	ret->right = NULL;
	return ret;
}
void test2()
{
	//手动创建一颗二叉树
	BTNode* n1 = BuyBTNode(1);
	BTNode* n2 = BuyBTNode(2);
	BTNode* n3 = BuyBTNode(3);
	BTNode* n4 = BuyBTNode(4);
	BTNode* n5 = BuyBTNode(5);
	BTNode* n6 = BuyBTNode(6);
	n1->left = n2;
	n2->right = n4;
	n2->left = n3;
	n4->left = n5;
	n4->right = n6;
	//该二叉树的根节点为n1
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

注意上面并不是建立二叉树的真正方式，只是我们为了演示和方便手动创建的一颗二叉树！

前序遍历

首先我们可以将一颗二叉树看成三部分：

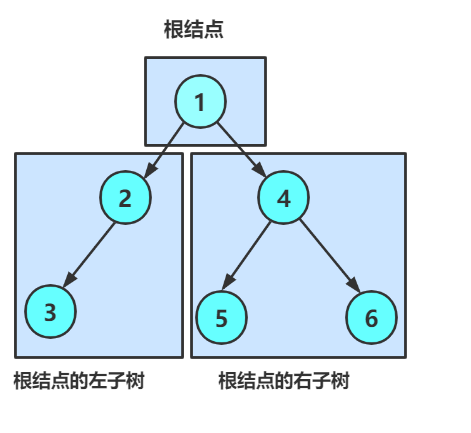
然后嘞左子树又可以看成三部分：

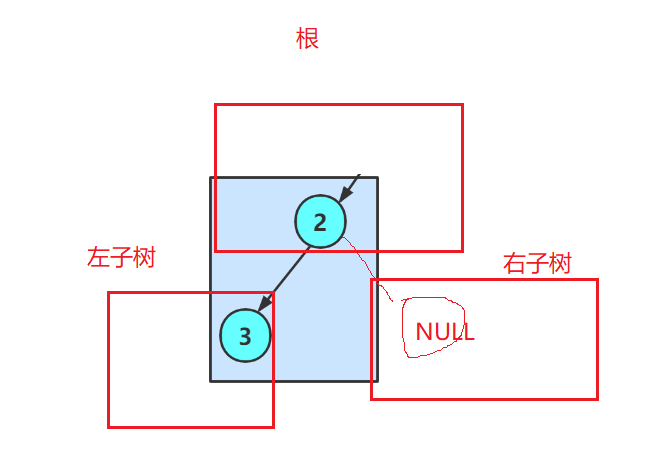
然后嘞我们的左子树又可以按照上面的规则又分为根、左子树、右子树！三个部分：

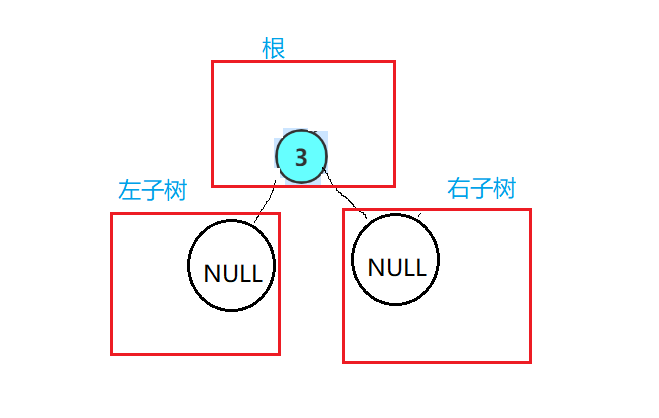
然后嘞我们再将左子树分：

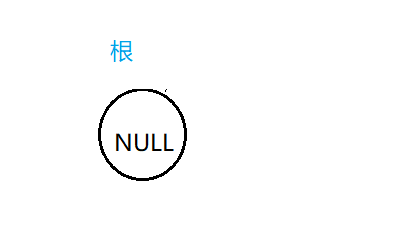
我们发现这时候左子树已经不能再向上面那样分为根、左子树、右子树三个部分了，只有根这一个部分，没有左子树、右子树了，我们称为这样的一颗树为空树，这样的话我们也就不能再向下分了；那么同理右子树也是这样的！！
-------------------------------------------------------------------------------------------------------------------------------------
现在我们回归主题，我们来谈一谈前序遍历！！
前序遍历的顺序：根、左子树、右子树；

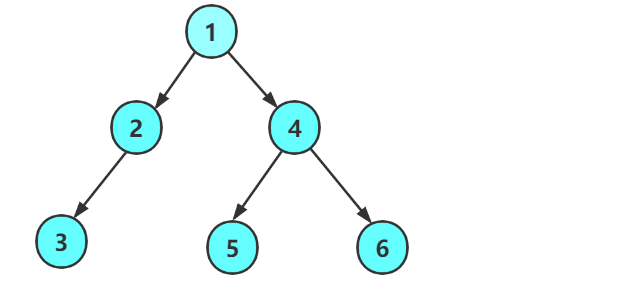
思路与上面是一样的！我们首先从root(根)入手，那么我们首先遇到的是根节点：

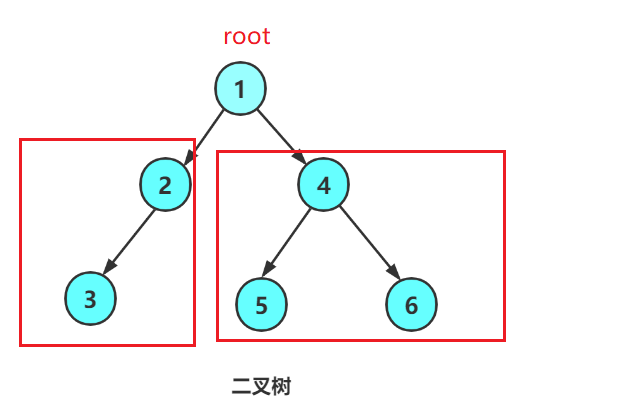
然后了我们将root节点的值打印一下！，我们再去遍历左子树，

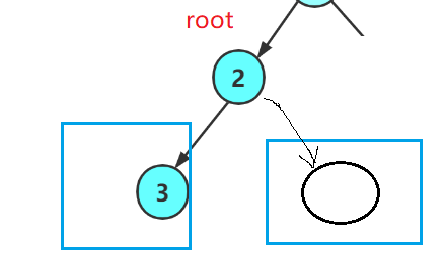
然后我们又遇到了左子树的根节点，我们再打印它，然后我们再去遍历当前二叉树的左子树：

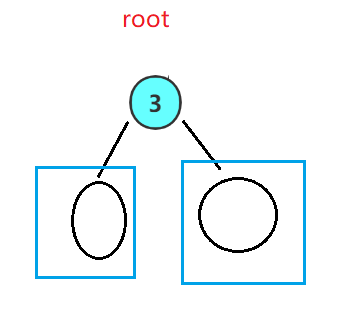
然后嘞我们再去遍历该二叉树的左子树：

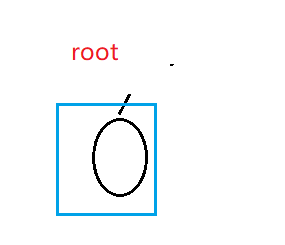
这时候我们已经到达了空树，我们已经无法再分了，我们直接返回即可；
然后嘞我们就会来到上一层，我们开始遍历上一层的右子树，右子树也是一颗树啊！！又可以分为根、左子树、右子树，就这样不断分下去……，最后会分到空树，我们就不在往下分，直接返回就好了！！！
代码方面：

// 二叉树前序遍历 
void BinaryTreePrevOrder(BTNode* root)
{
	if (!root)//如果是空树直接返回，不要再分了！！
	{
    printf("NULL ");
	return;
	}
	printf("%d ",root->val);
	BinaryTreePrevOrder(root->left);//去遍历左子树
	BinaryTreePrevOrder(root->right);//左子树遍历完，我们再去遍历右子树
}
1
2
3
4
5
6
7
8
9
10
11
12

为了便于理解这个过程，我们来画一画这个递归展开图：

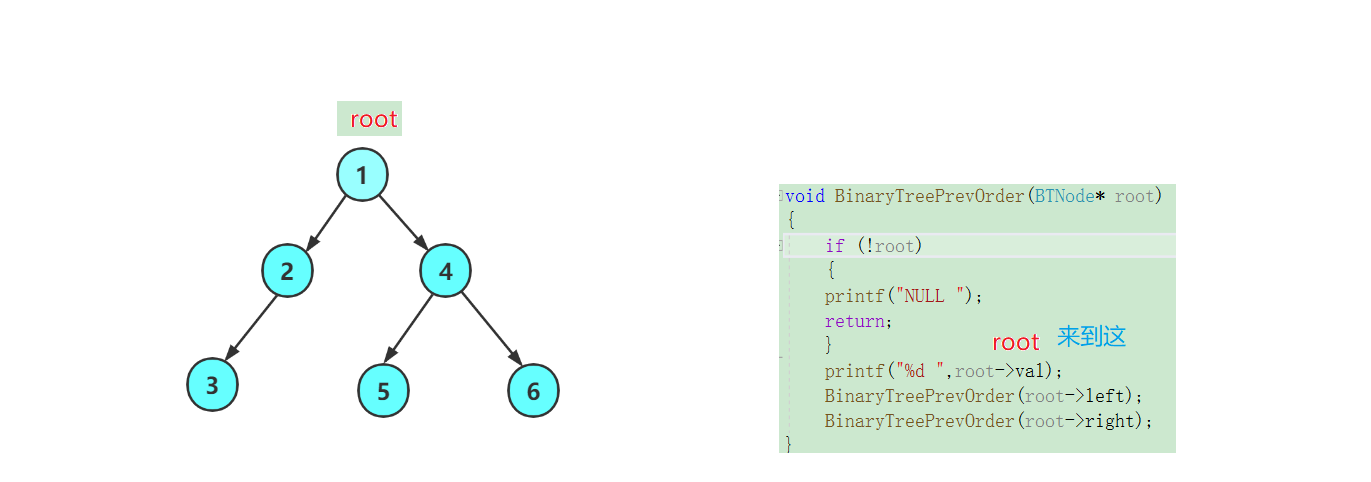
我们打印一下root指向的节点的值：1，然后我们去访问该二叉树的左子树！

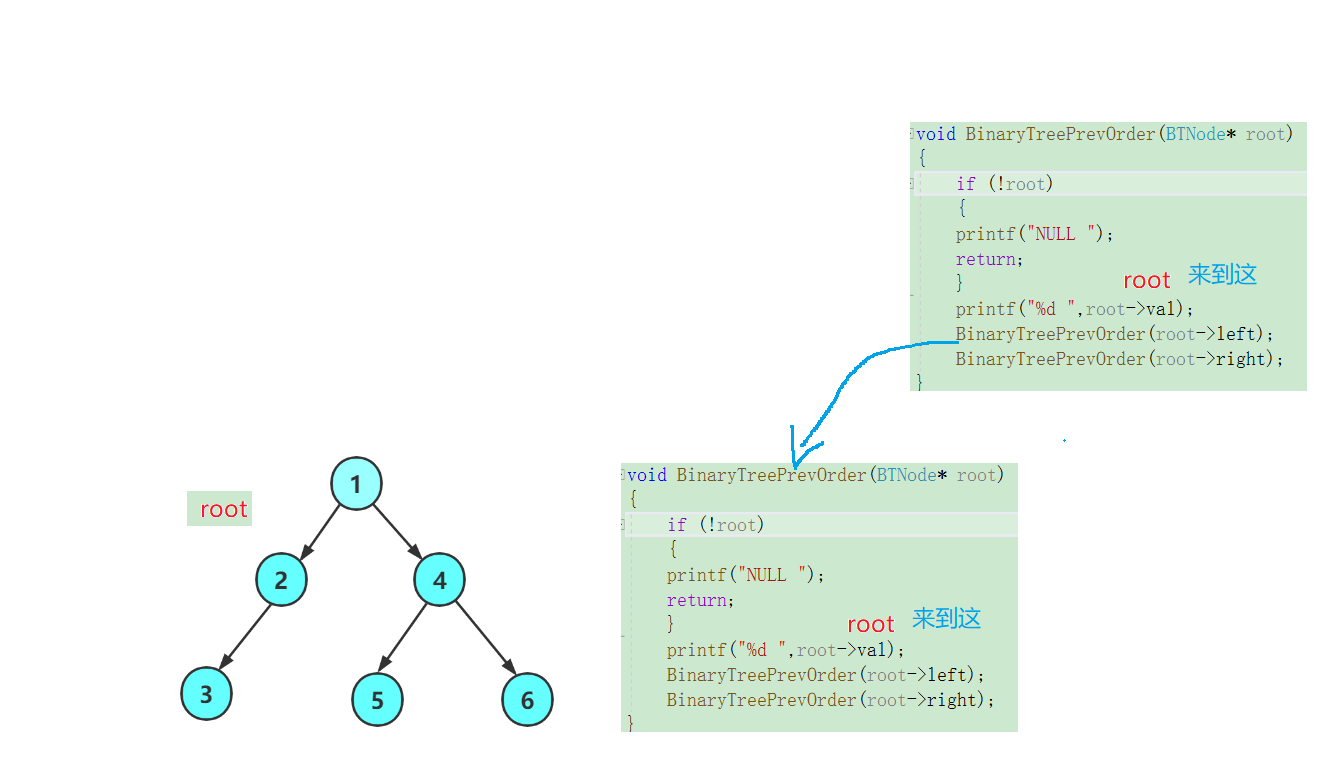
我们打印一下：2，然后我们去访问该二叉树的左子树！

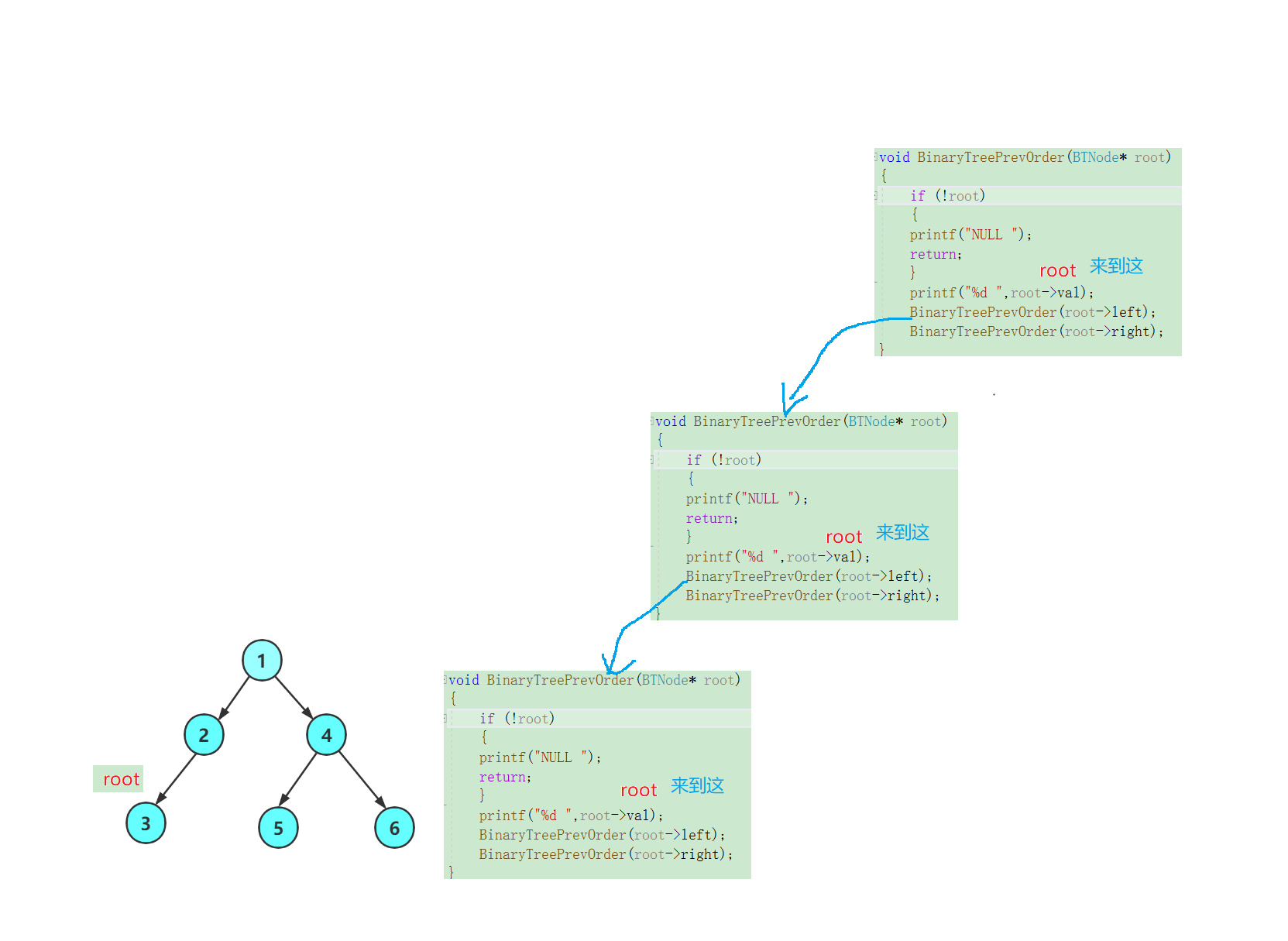
我们打印一些根节点，然后访问其左子树：

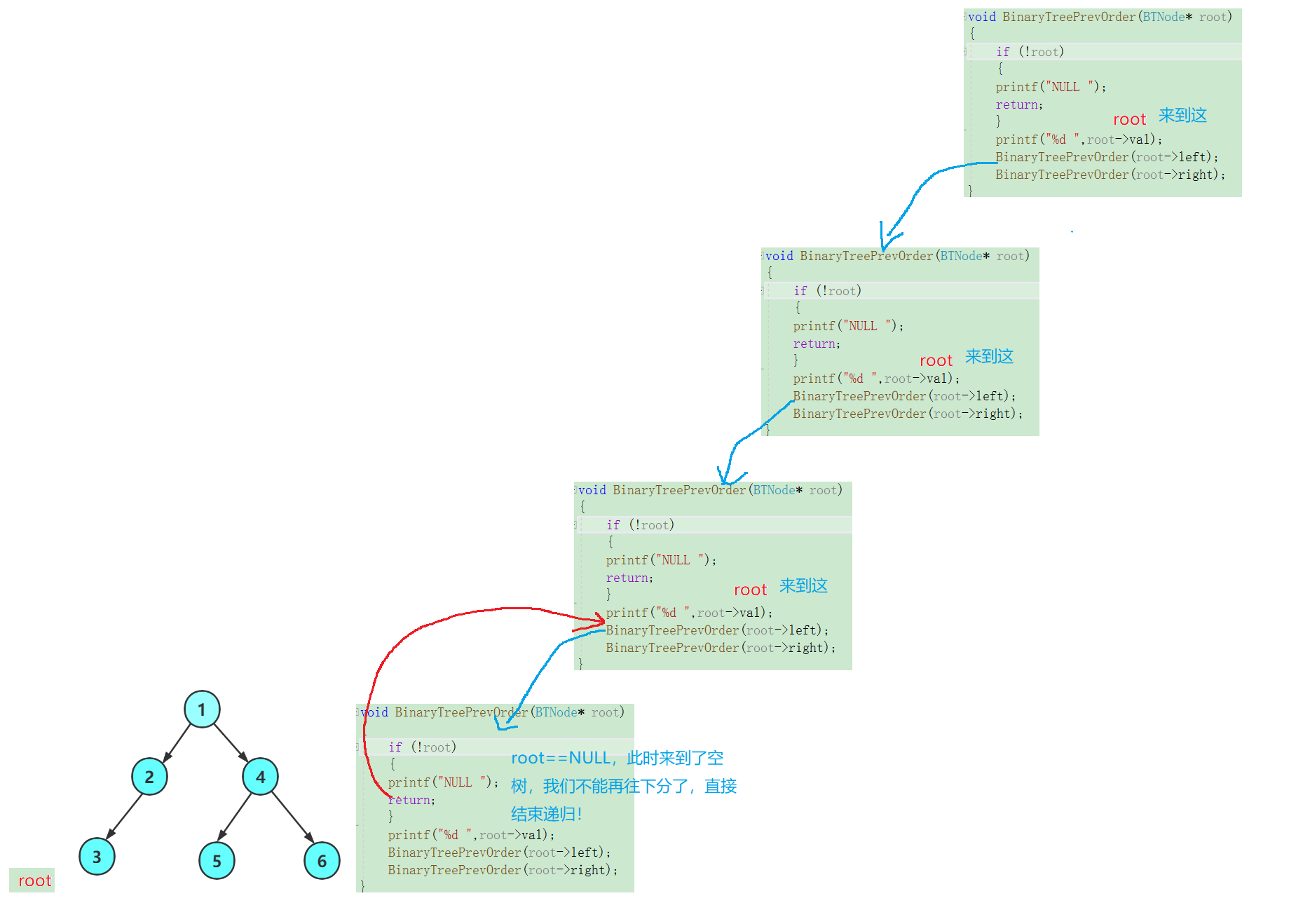
来到空树我们就返回上一层，并且开始遍历上一层的右子树：

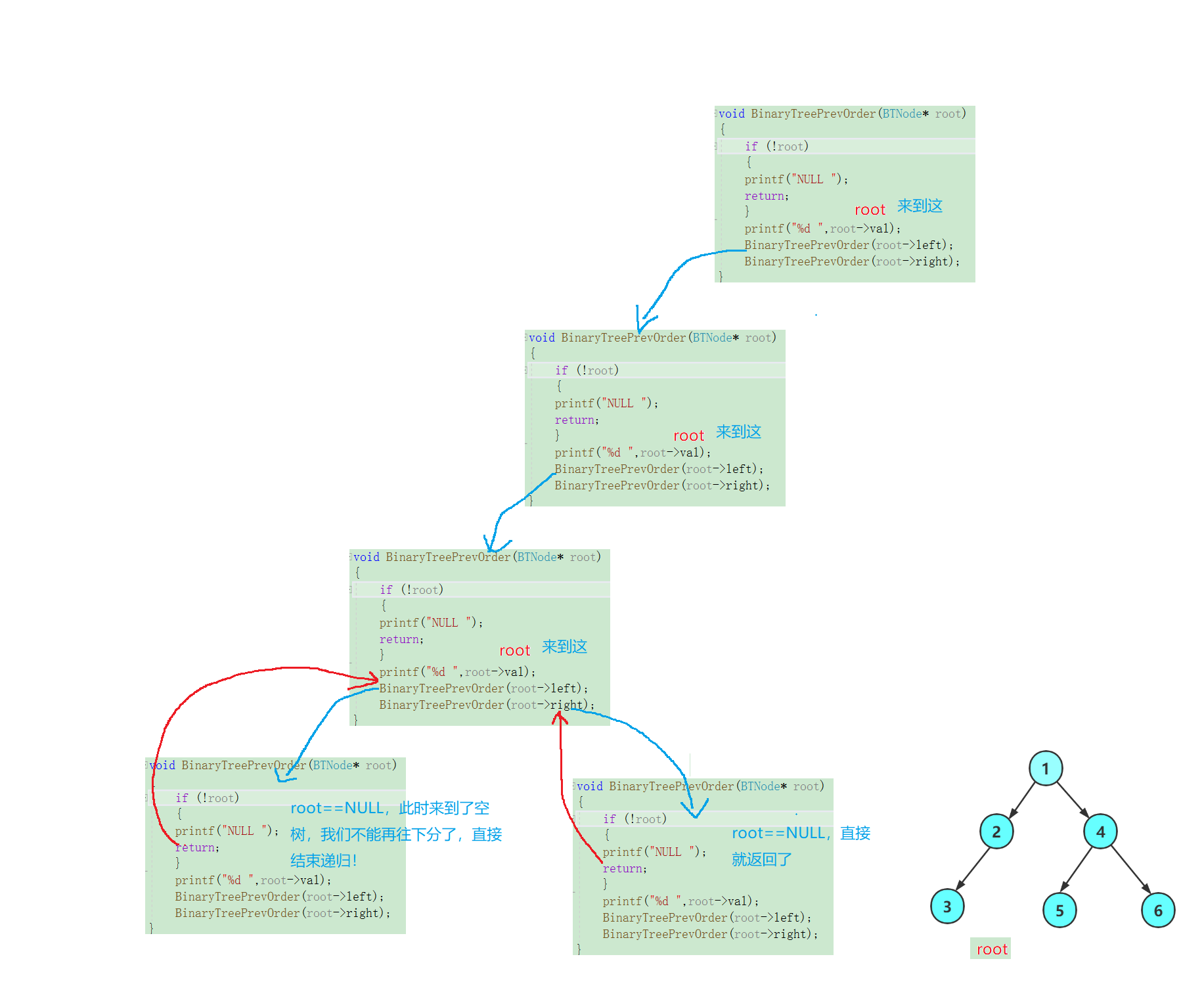
这时，3的右子树也为NULL，不能再分了，直接返回！！，这是2的左子树就已经遍历完了，我们该开始遍历2的右子树了！

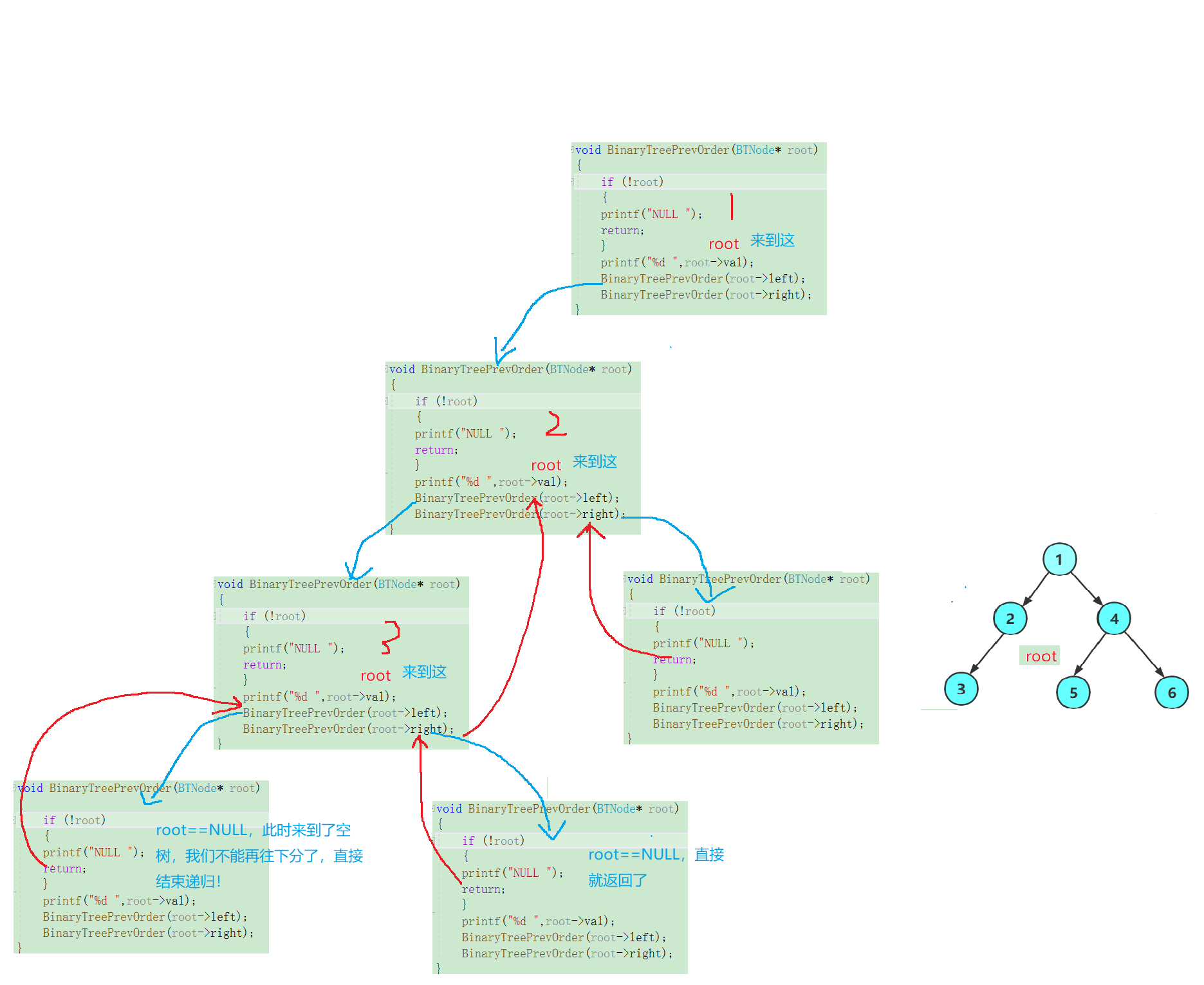
2的右子树为空，不可再分，直接返回，这是1的左子树被遍历完了，我们再来访问1的右子树：

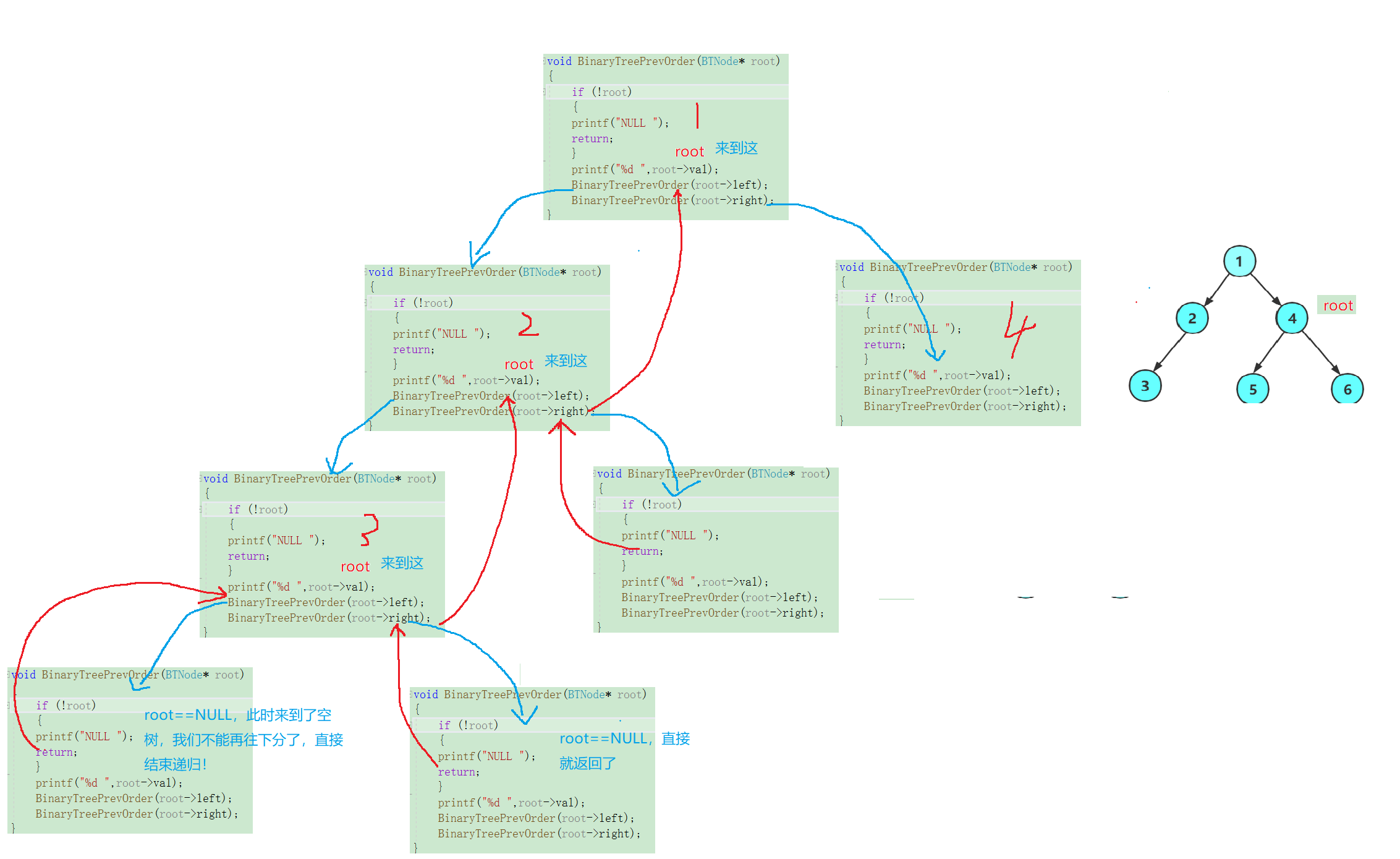
这时进来4又可以分为根、左子树、右子树，我们来访问4的左子树：

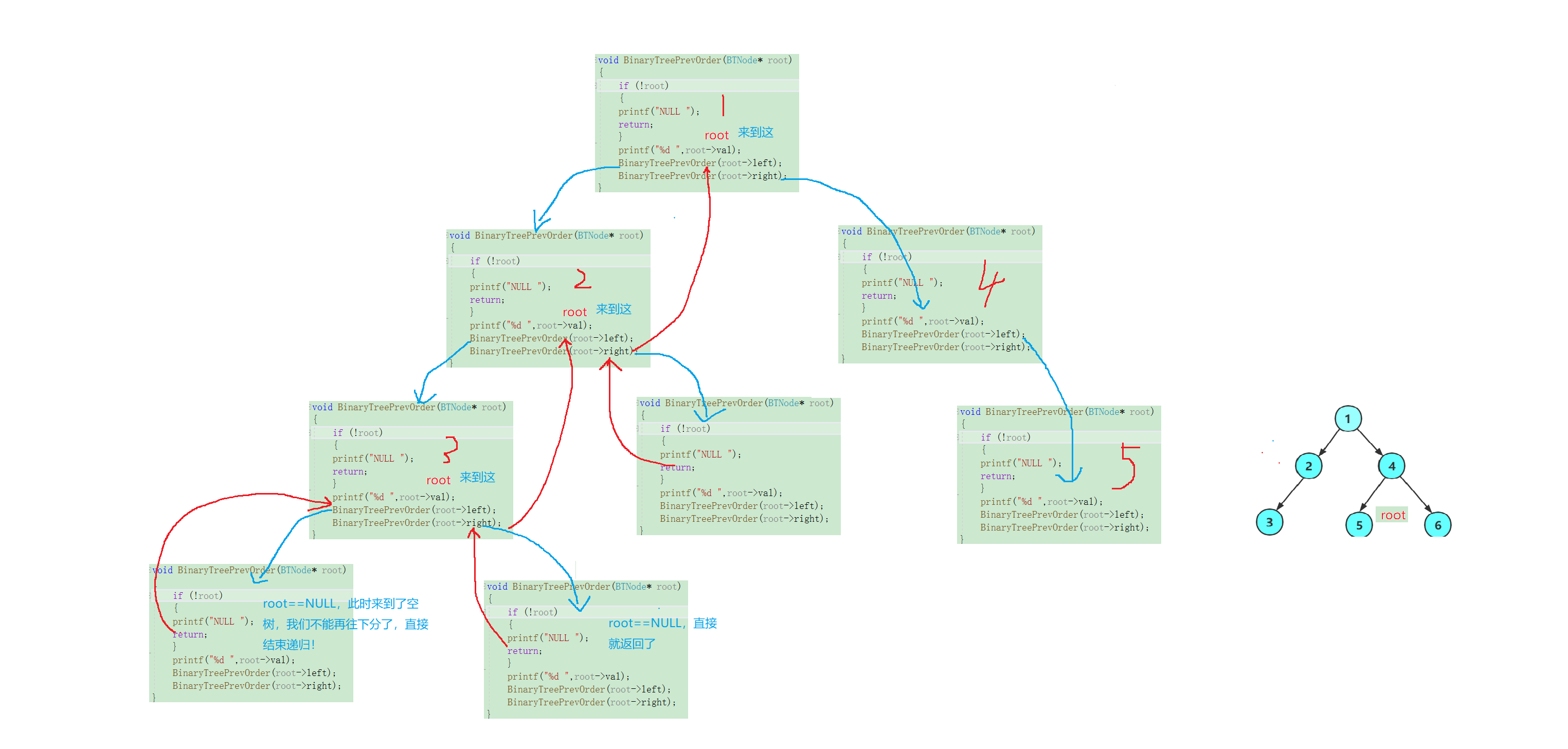
这时我们进来，又是一颗以5为根的树，又可以分为：根、左子树、右子树：
我们按照前序遍历的规则，根被访问完了，我们立马去访问左子树：

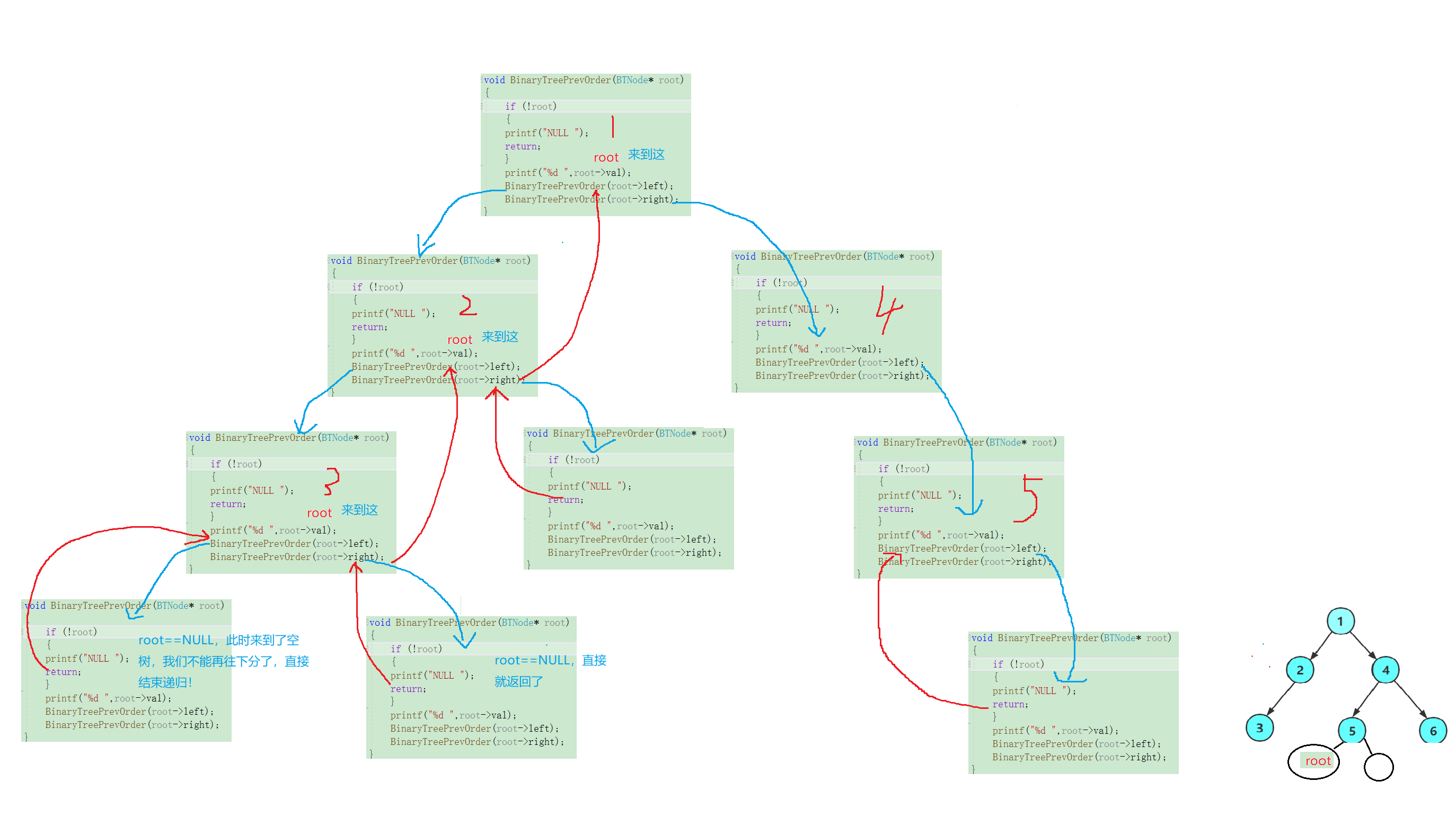
这时遇到了空树，直接返回就好，那么这时候回到上一层过后，就代表着5的左子树已经访问完毕了，接下来改访问5的右子树了：

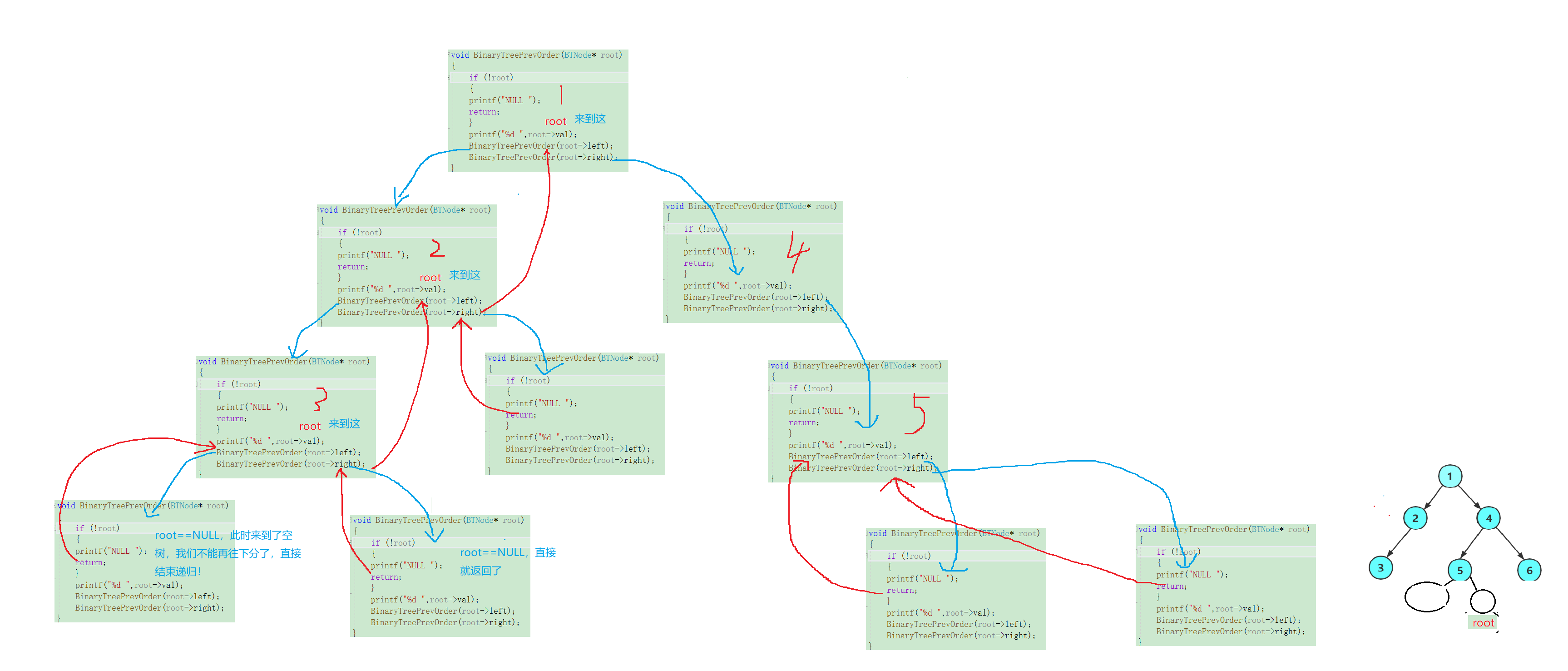
很好，此时5的右数也为空，我们直接返回就好，至此，代表着5的左右子树都已经遍历完毕（也可以了理解为4的左子树遍历完毕！），那么这时候我们就会返回5的上一层，开始遍历4的右子树：

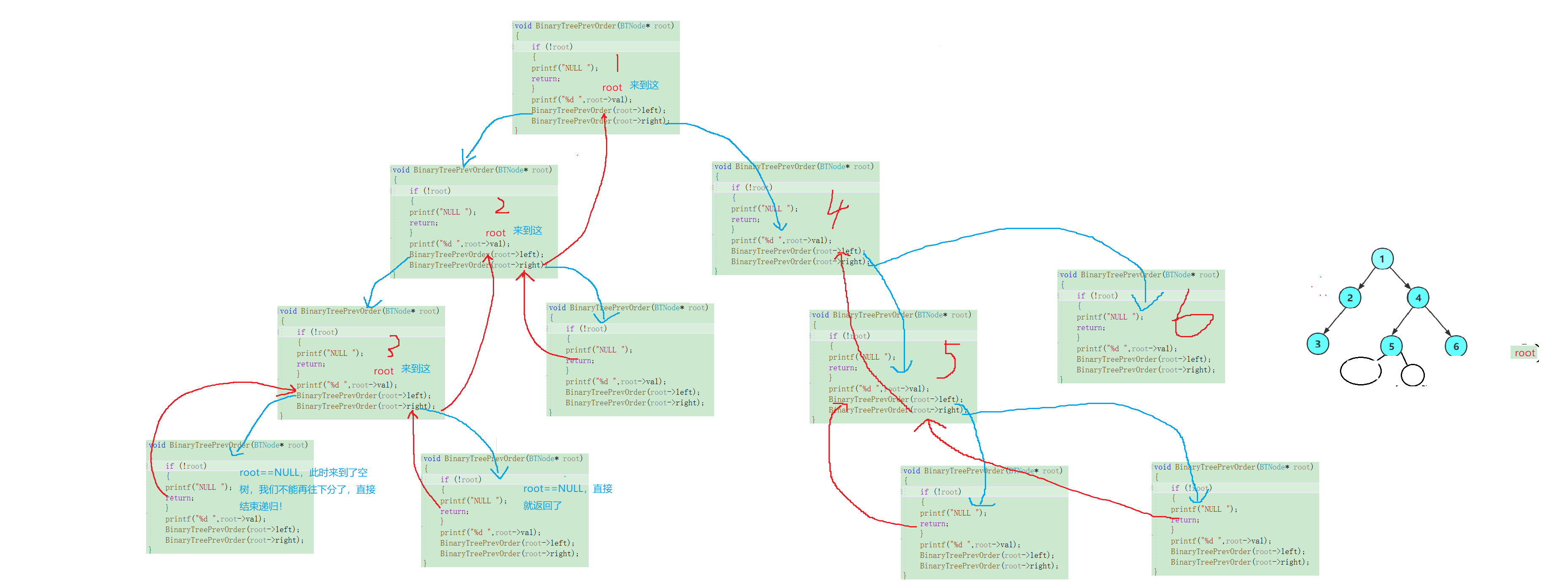
这时候我们就来到了以6为根节点的二叉树，我们此时按照规则，先访问根节点、再访问左子树、右子树，现在我们开始访问6的左子树：

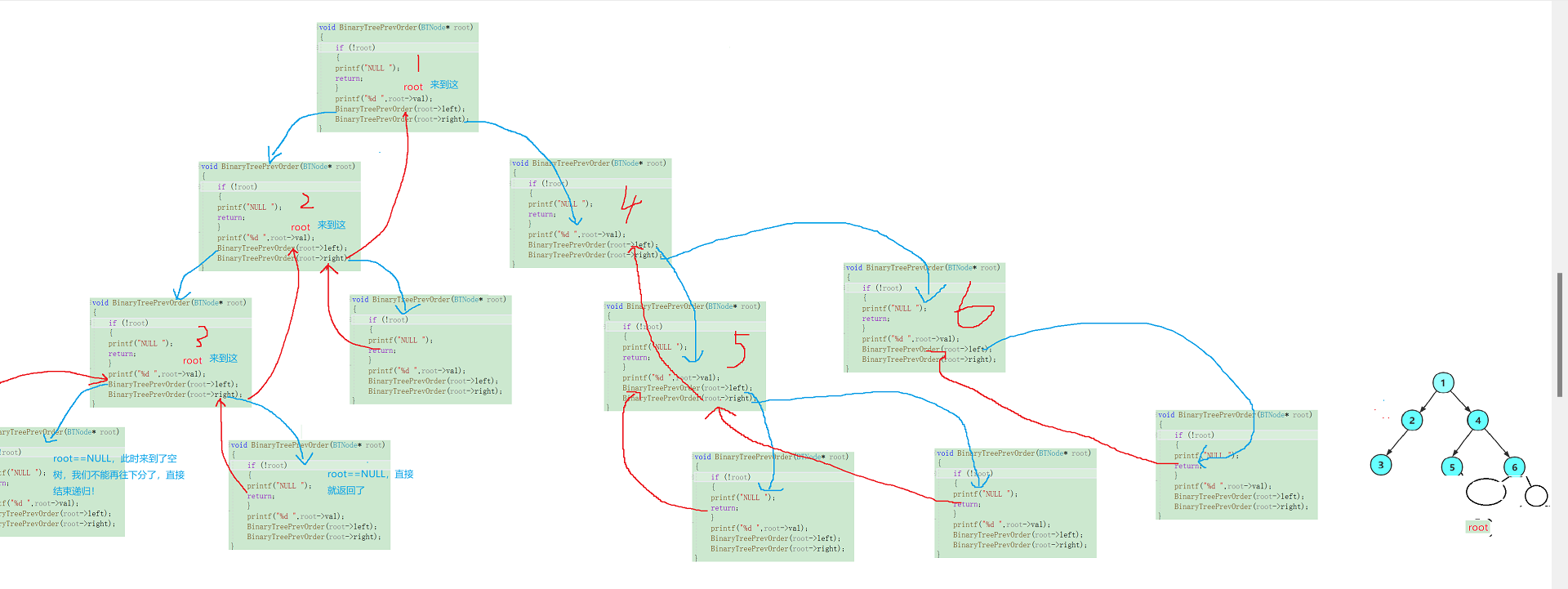
我们发现6的左子树是空树，直接返回到上一层，此时6的左子树数被遍历完毕！，接下来改变了6的右子树：

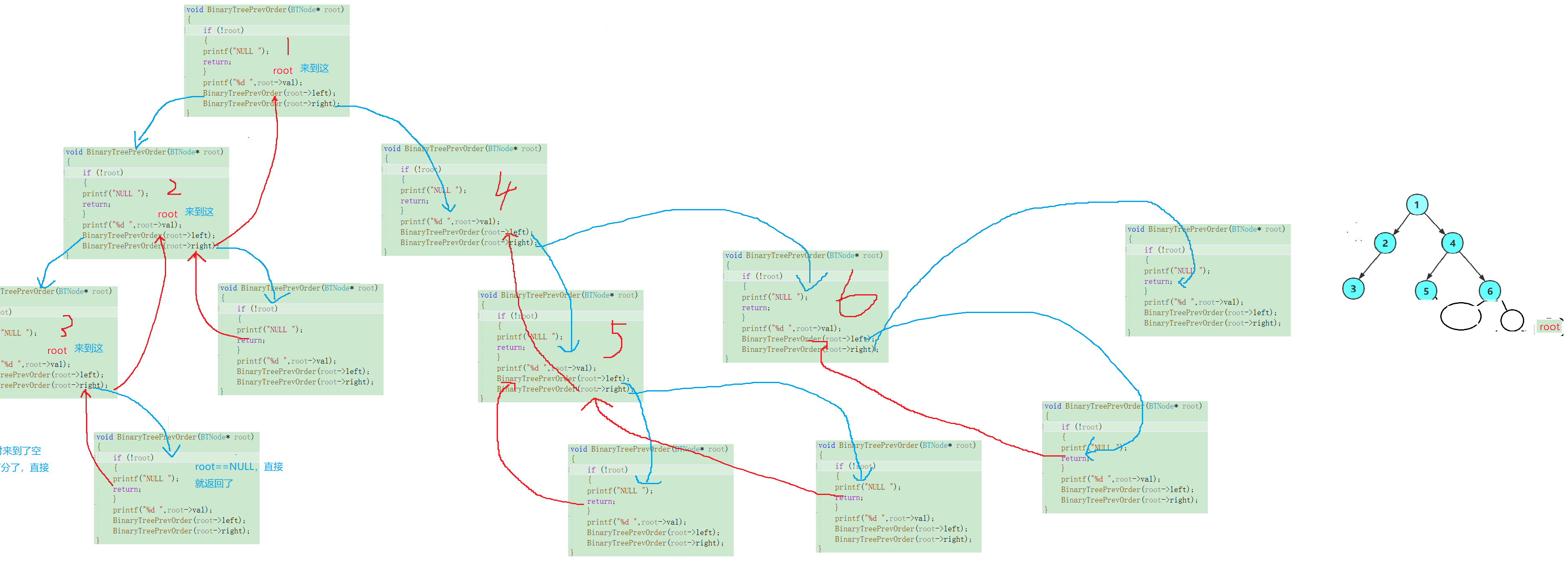
6的右子树也是空树，我们直接返回，至此6的左子树右子树被遍历完毕，也可以说6这颗二叉树被遍历完毕，也可以说是4的右子树遍历完毕，那么附带一些列的连锁反应，4这整颗数也被访问完毕，1的右子树被访问完毕！，1这整颗树被访问完毕！，整颗二叉树被访问完毕！，至此整个递归过程结束：
全家福：

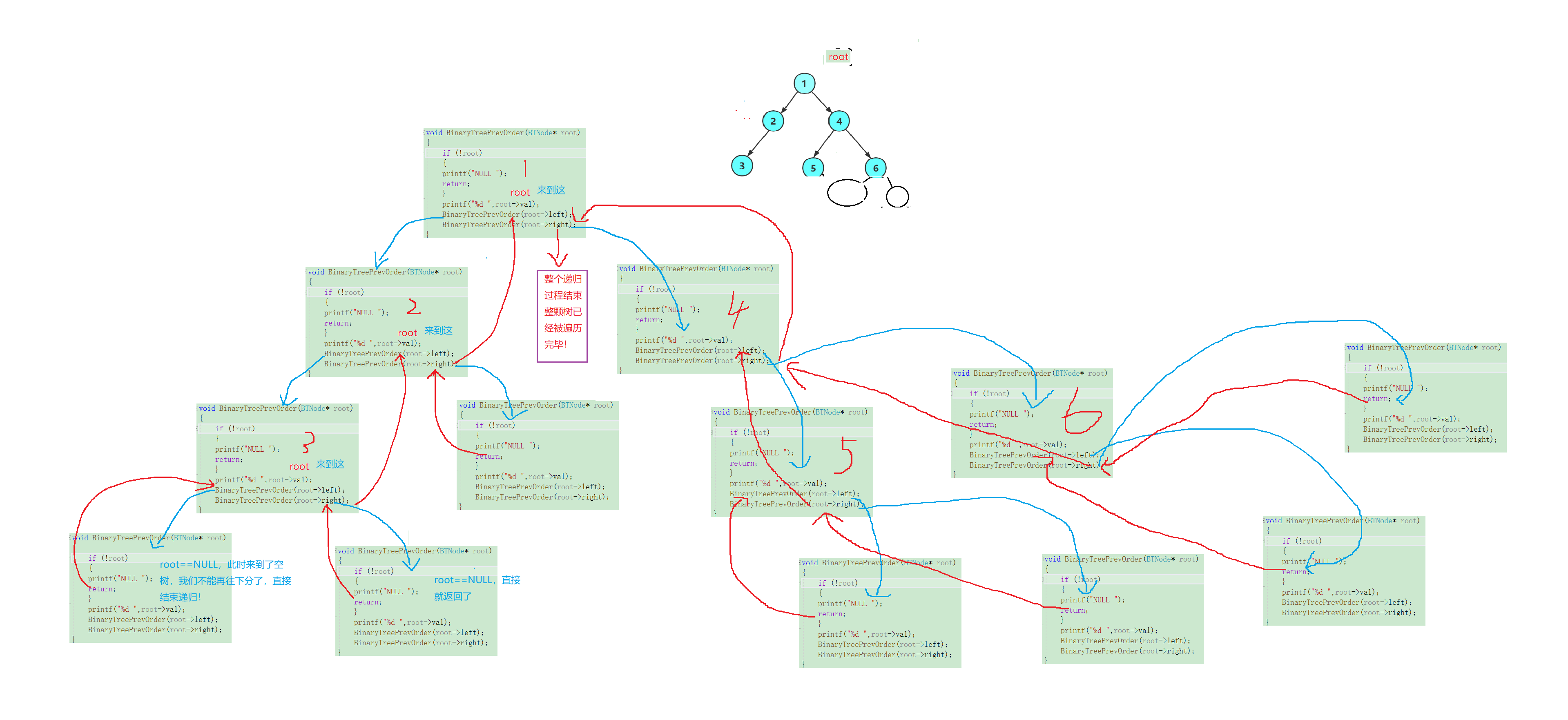
画的可能有点乱，但是我们整体看起来这个递归过程也是像一颗二叉树！！
（要注意其中箭头指向的位置和开始位置！！）

其实递归嘞，就是先将这个函数当作已知条件，先假设我们递归了自己会得到一个什么样的结果，然后再根据这个结果去做后面的操作就行了，我们再设计算法的时候，不必在意函数递归调用的细节，你就认为我只要将参数交给这个函数，就能得到想要的结果，然后根据结果再设计接下来的操作就可以了！！，比如前序遍历：我们知道这个函数的功能是遍历真个二叉树，那么我们先访问根节点，然后我们再去前序遍历左子树，我们只需将参数交给递归调用的函数就可以，不必关系它具体是怎末实现的！！然后假设交给它过后我们已经遍历完左子树了，然后同理将右子树的参数传给它，我们就完成了前序遍历！

中序遍历

中序遍历：左子树、根、右子树
我们只要弄懂前、中、后中随意一个遍历，那么另外两个就是手到擒来的事了：
还是跟上面一样我们已经知道这个函数的功能了，以中序遍历二叉树，那么我们先将左子树的参数给他，默认他已经帮我们完成了，我们紧接着打印根节点，然后同样的道理让其帮我遍历右节点：

// 二叉树中序遍历
void BinaryTreeInOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	BinaryTreeInOrder(root->left);
	printf("%d ",root->val);
	BinaryTreeInOrder(root->right);
}
1
2
3
4
5
6
7
8
9
10
11
12

后序遍历

后序遍历：左子树、右子树、根

// 二叉树后序遍历
void BinaryTreePostOrder(BTNode* root)
{
	if (!root)
	{
		printf("NULL ");
		return;
	}
	BinaryTreePostOrder(root->left);
	BinaryTreePostOrder(root->right);
	printf("%d ", root->val);

}
1
2
3
4
5
6
7
8
9
10
11
12
13

层序遍历

层序遍历不同前面的遍历，层序遍历再有些地方也叫做广度优先遍历，那么这个遍历是个啥意思嘞：

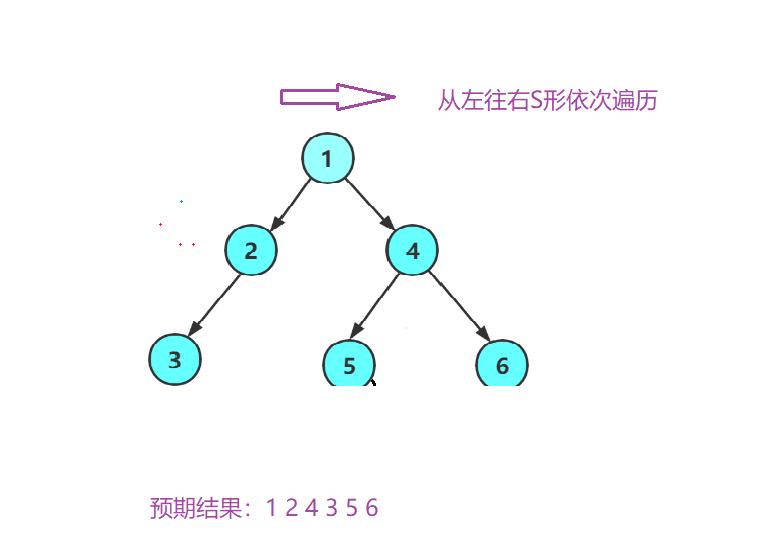
在这里呢我们需要借助一下队列来实现：
大致思路：

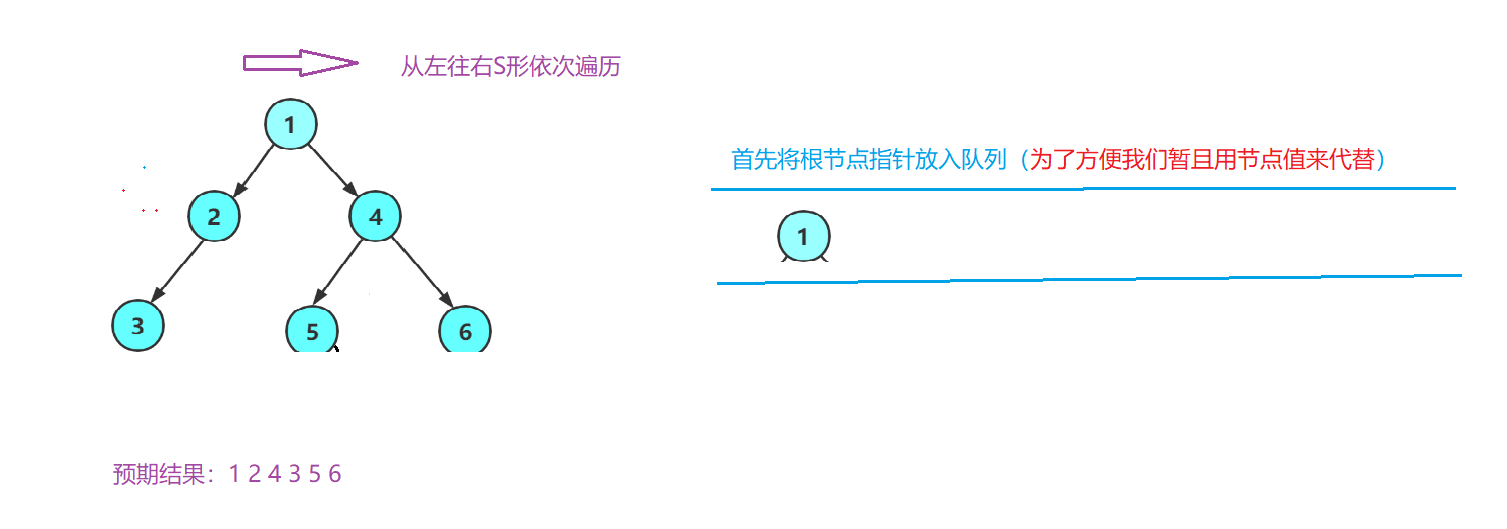
然后呢，我们取出队头，并且删掉队头数据！然后打印一下取出来的节点数据，然后呢我们再将该节点的所有孩子节点全部入队（有就入，没有就不入）

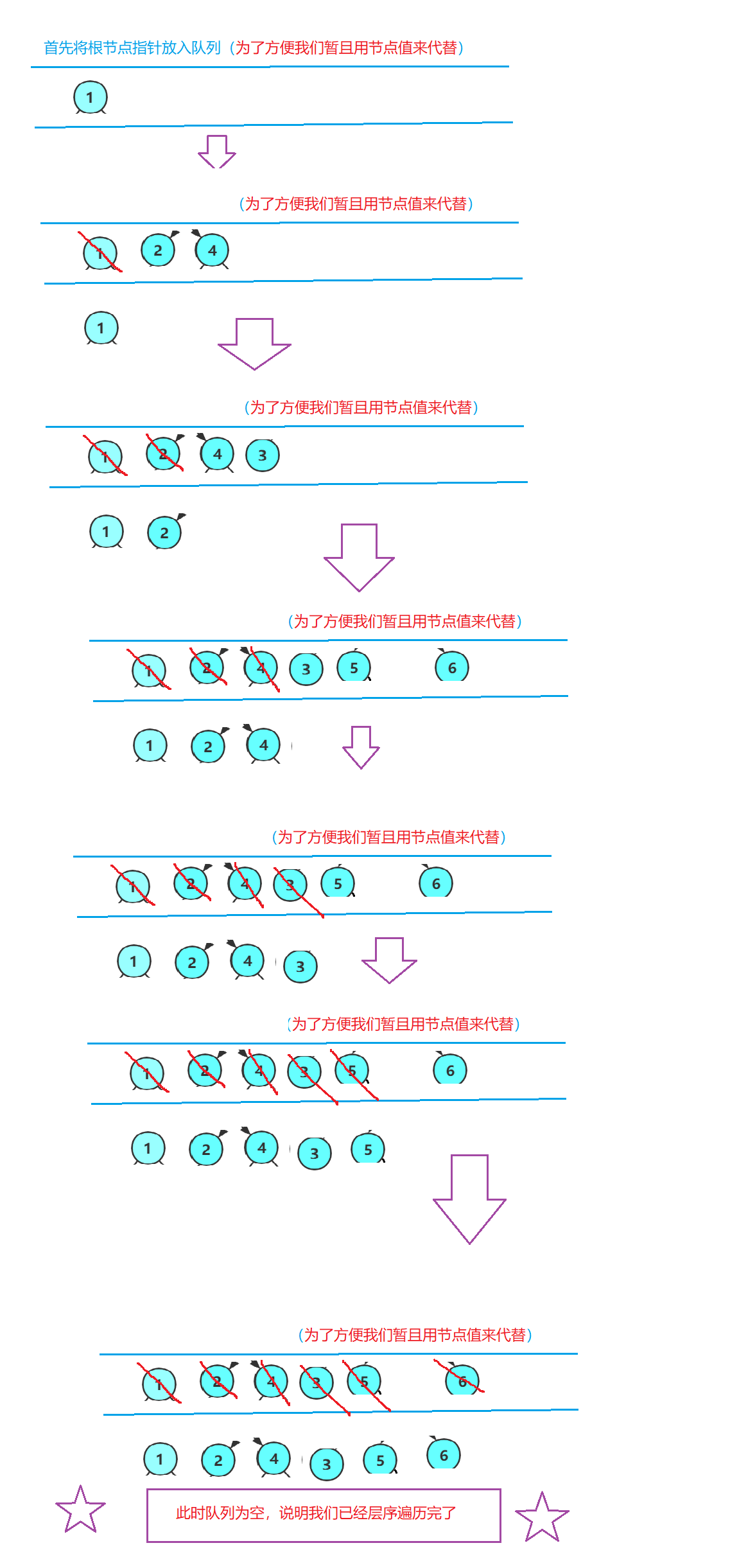
代码方面：

// 层序遍历
void BinaryTreeLevelOrder(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q,root);
	while (QueueEmpty(&q)==false)
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		printf("%d ",front->val);
		if (front->left)
			QueuePush(&q,front->left);
		if (front->right)
			QueuePush(&q,front->right);
	}
	QueueDestroy(&q);
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18

如何判断一颗二叉树是完全二叉树

首先我们得知道完全二叉树的概念：

完全二叉树是效率很高的数据结构，完全二叉树是由满二叉树而引出来的。对于深度为K
的，有n个结点的二叉树，当且仅当其每一个结点都与深度为K的满二叉树中编号从1至n的结点一一对
应时称之为完全二叉树。

其中完全二叉树有一个很重要的概念！连续！！！
只要不是完全二叉树，那么一定不是连续的比如：

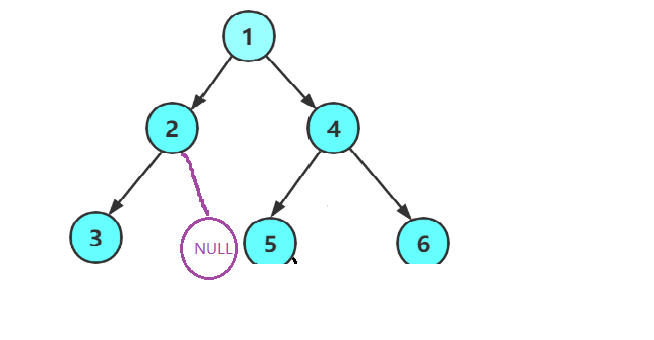
上面就不是一颗完全二叉树！
那么如果我们每一个节点，每一个节点的去验证，当我们遇到NULL指针节点时，我们验证一下其后面还有没有有效节点，如果没有则说明这是一颗完全二叉树；若有，则说明这不是一颗完全二叉树；
这里遍历每一个节点和判断NULL节点后面有没有有效值，我们需要借助层序遍历的思想：

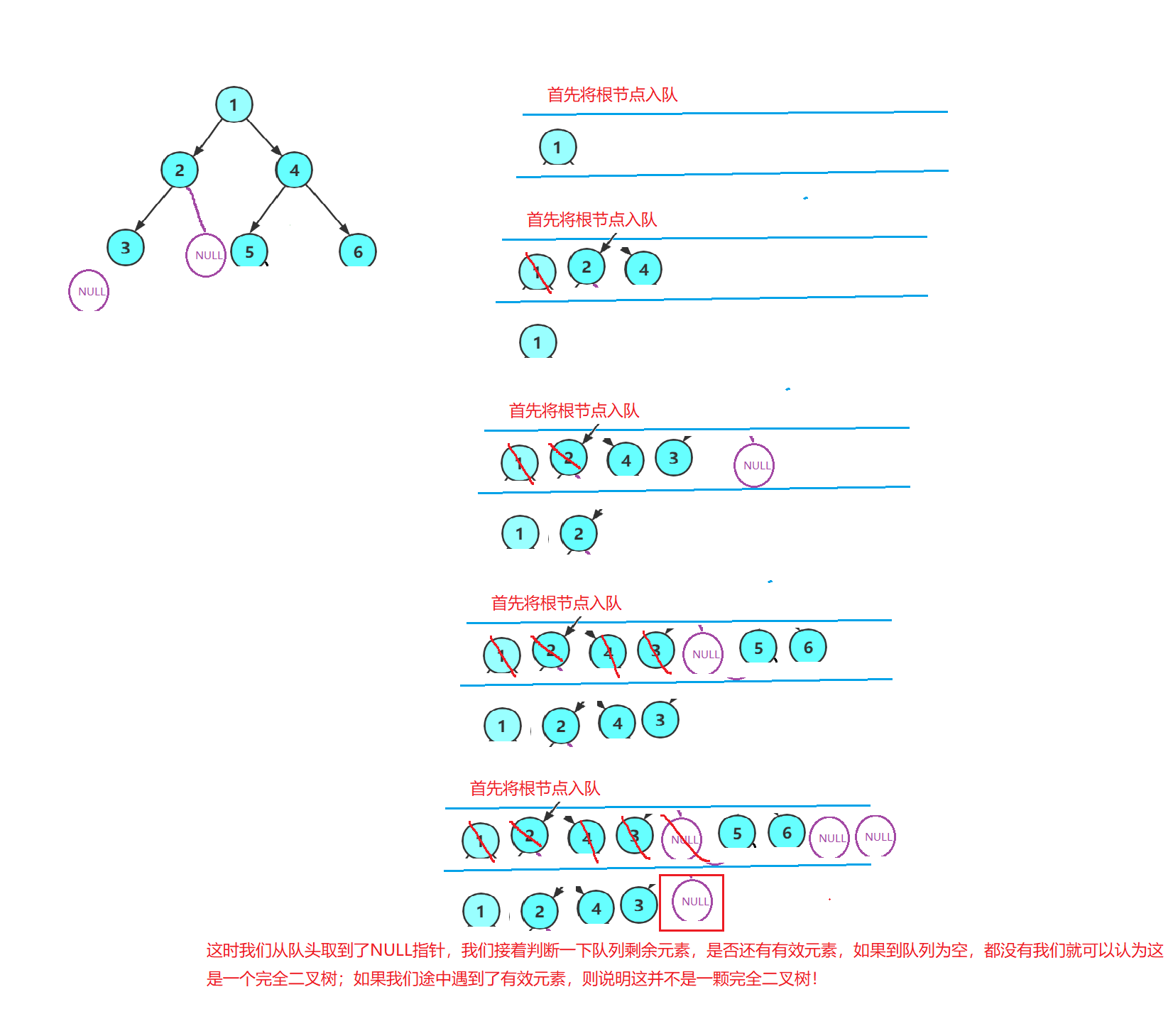
代码实现：

// 判断二叉树是否是完全二叉树
bool BinaryTreeComplete(BTNode* root)
{
	Queue q;
	QueueInit(&q);
	QueuePush(&q,root);
	while (1)
	{
		BTNode* front = QueueFront(&q);
		QueuePop(&q);
		if (front)
		{
			QueuePush(&q,front->left);
			QueuePush(&q,front->right);
		}
		else
		{
			while (QueueEmpty(&q) == false)
			{
				if (QueueFront(&q))
					return false;
				else
					QueuePop(&q);
			}
			return true;
		}
	}
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

现在我们来解释一下，为什么只要NULL指针之后如果没有有效元素的话，他就是一颗完全二叉树！万一后面还有元素只是还没来到及入队嘞，我们的判断是不是过早了？
首先我们将每个节点的孩子节点都画出来（包括空孩子）

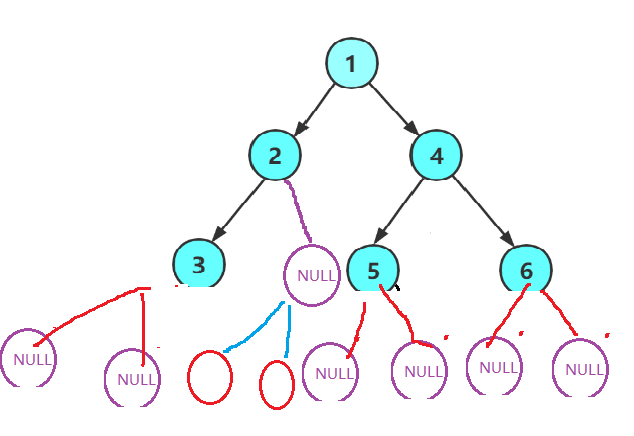
从图中我们可以知道再队列中的元素一定是队头元素的兄弟节点和它（比它大的兄弟节点的孩子节点），就比如图中，假设现在我队头元素就是第3层的空指针，那么此时队列中存在元素依次是5、6
、NULL、NULL此时不会有队头元素的孩子节点（因为我队头元素都还没有出队，自然也就不可能让孩子进队）！！那么这时候你在仔细品一品，假设我这事颗完全二叉树，那么我停下来判断的话，一定是在如下位置：

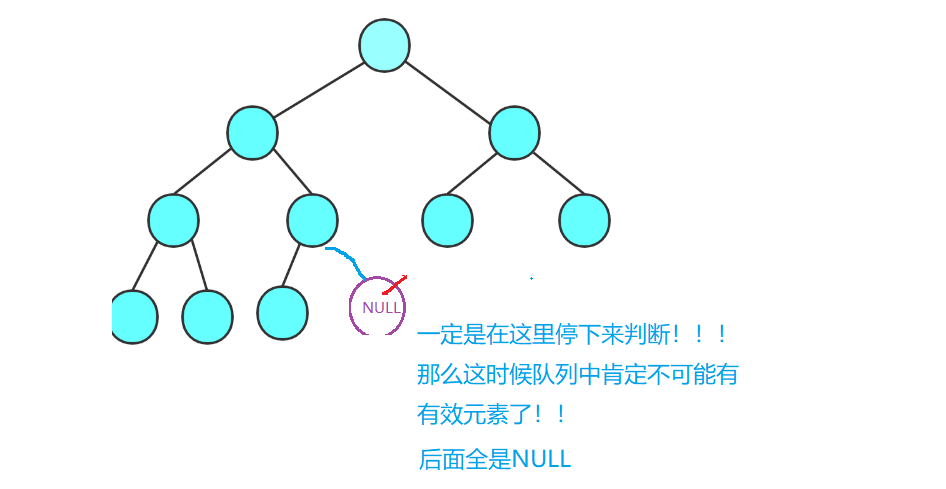
但是如果不是一颗完全二叉树的话，那么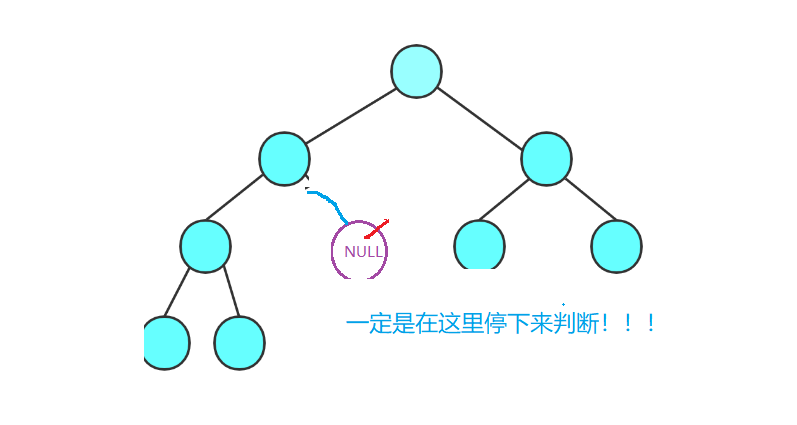
我们刚才上面分析了，队列中一定存的是，队头元素以后的兄弟节点和队头元素以前的兄弟节点的孩子节点！这两部份！！现在我们是遇到NULL指针才队列中的元素，如果队列中不存在队头节点以后的兄弟节点的话，同时也不存在队头节点以前的兄弟节点的孩子节点的话，那么队列中存的就全是NULL，那么这时候判断出来就是一颗完全二叉树；如果队列中存在两部分中任意一部分的有效节点，那么对不起，这不是一颗完全二叉树！！
---------------------------------------------------------------------------------------------------------
以上便是博主对于如何判断完全二叉树的愚见！欢迎大家指正！

通过前序遍历的数组构建二叉树

就比如：
“ABD##E#H##CF##G##”
#:代表NULL
是通过前序遍历出来的结果，我们现在想要通过这个结果，逆推回二叉树：
这道题还是递归：
根据我们上面书写前序遍历算法的经验：
我们假设一个函数是通过前序遍历创建二叉树的：
那么根据前序遍历的规则我们首先建立一个根节点，现在接下来就是构建左子树和右子树了，我们将数据交给这个函数，让它帮我们完成即可，我们无需关系其中细节：
画图再理解一下：

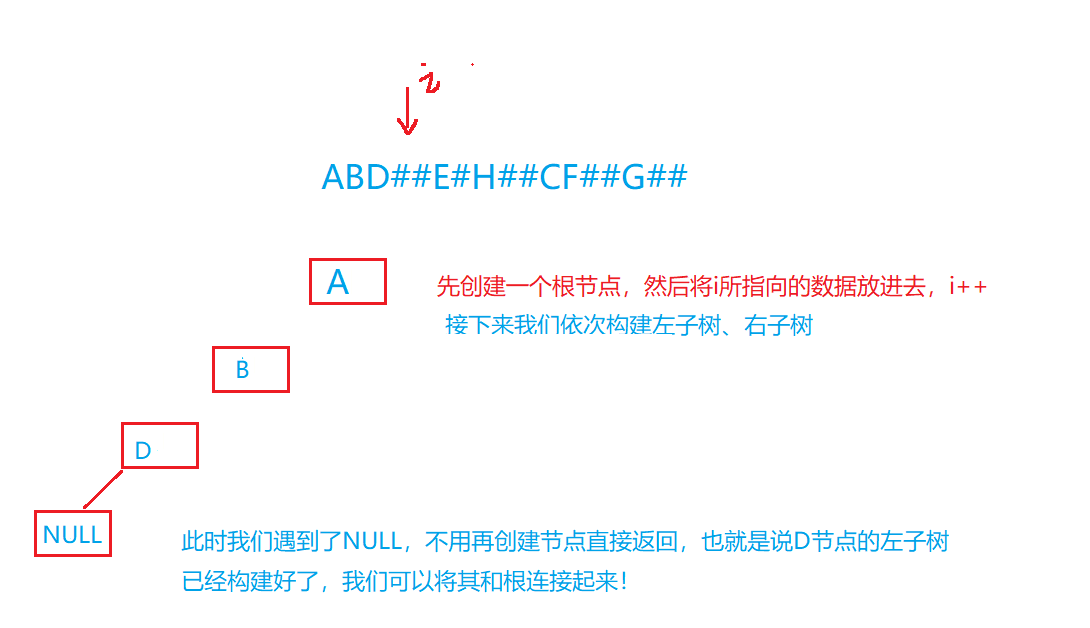
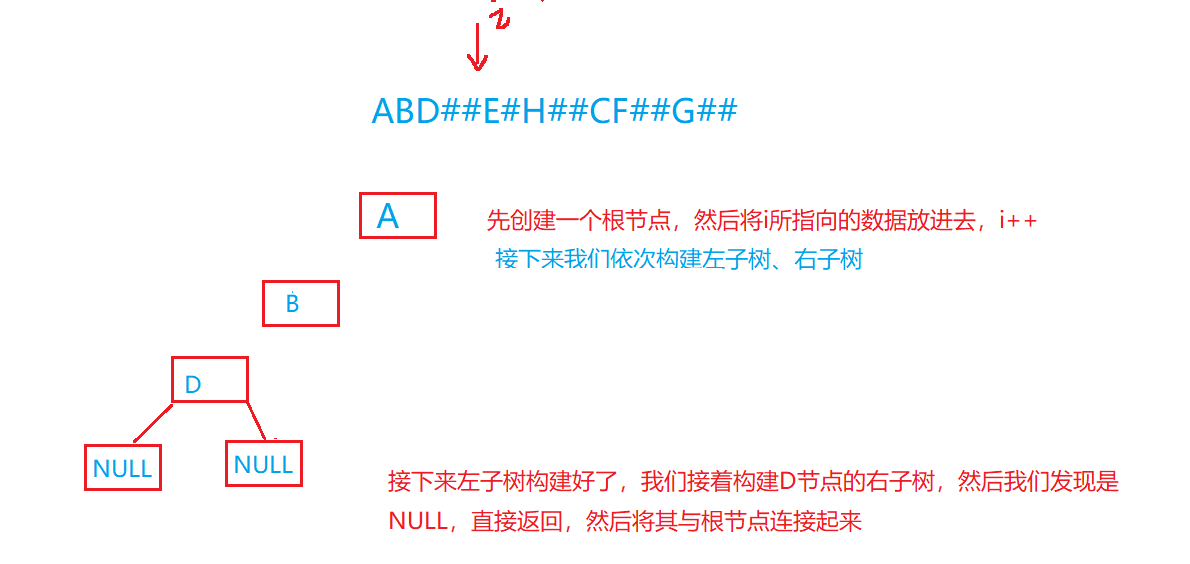
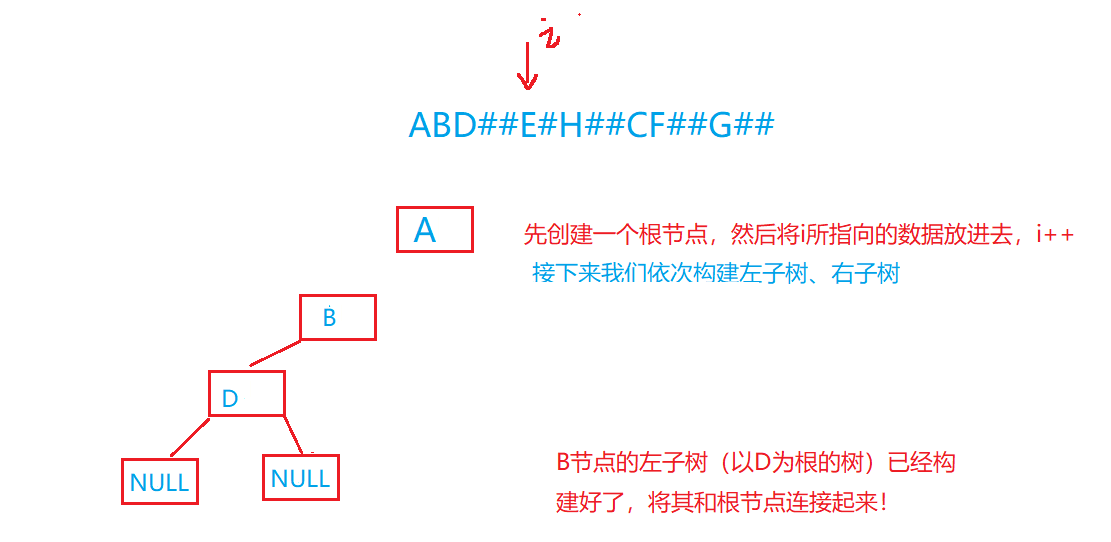
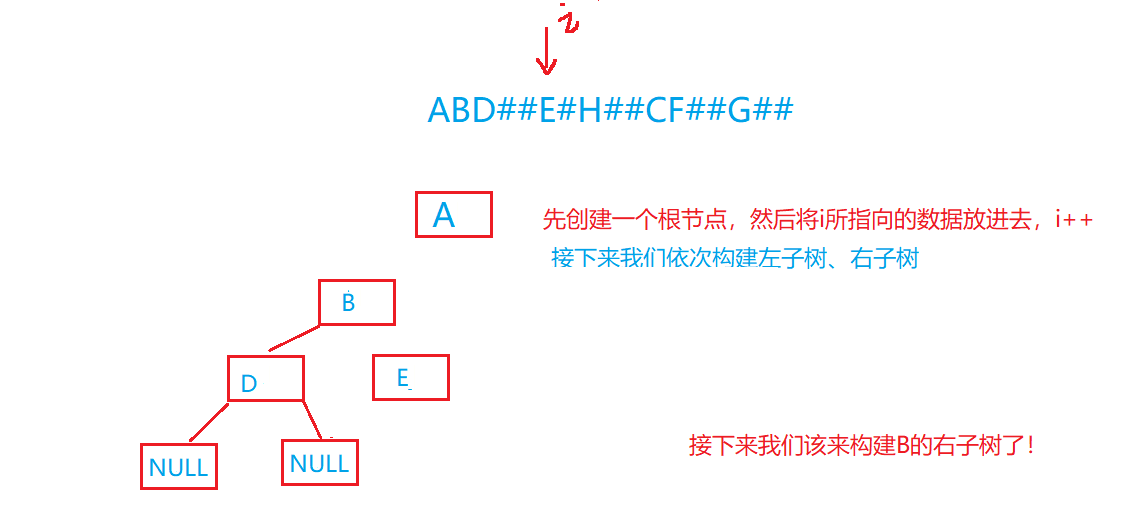
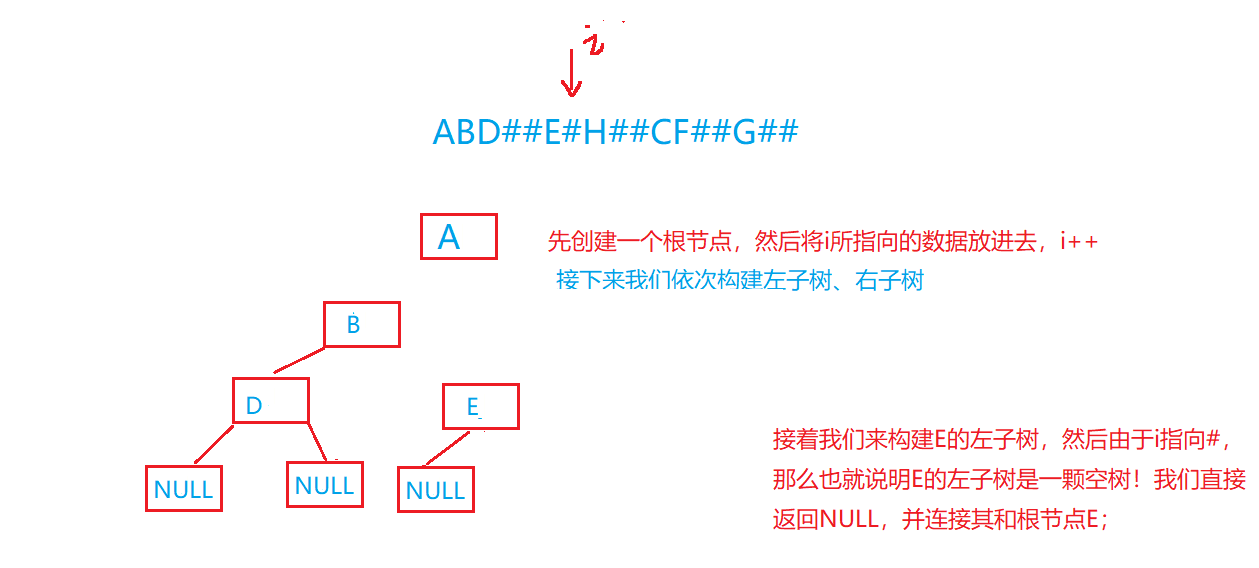
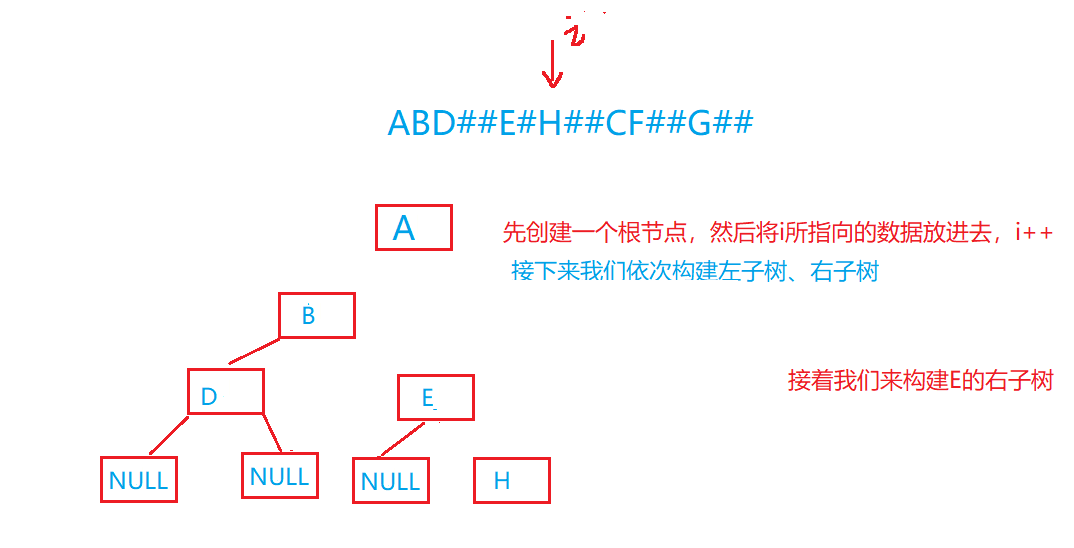
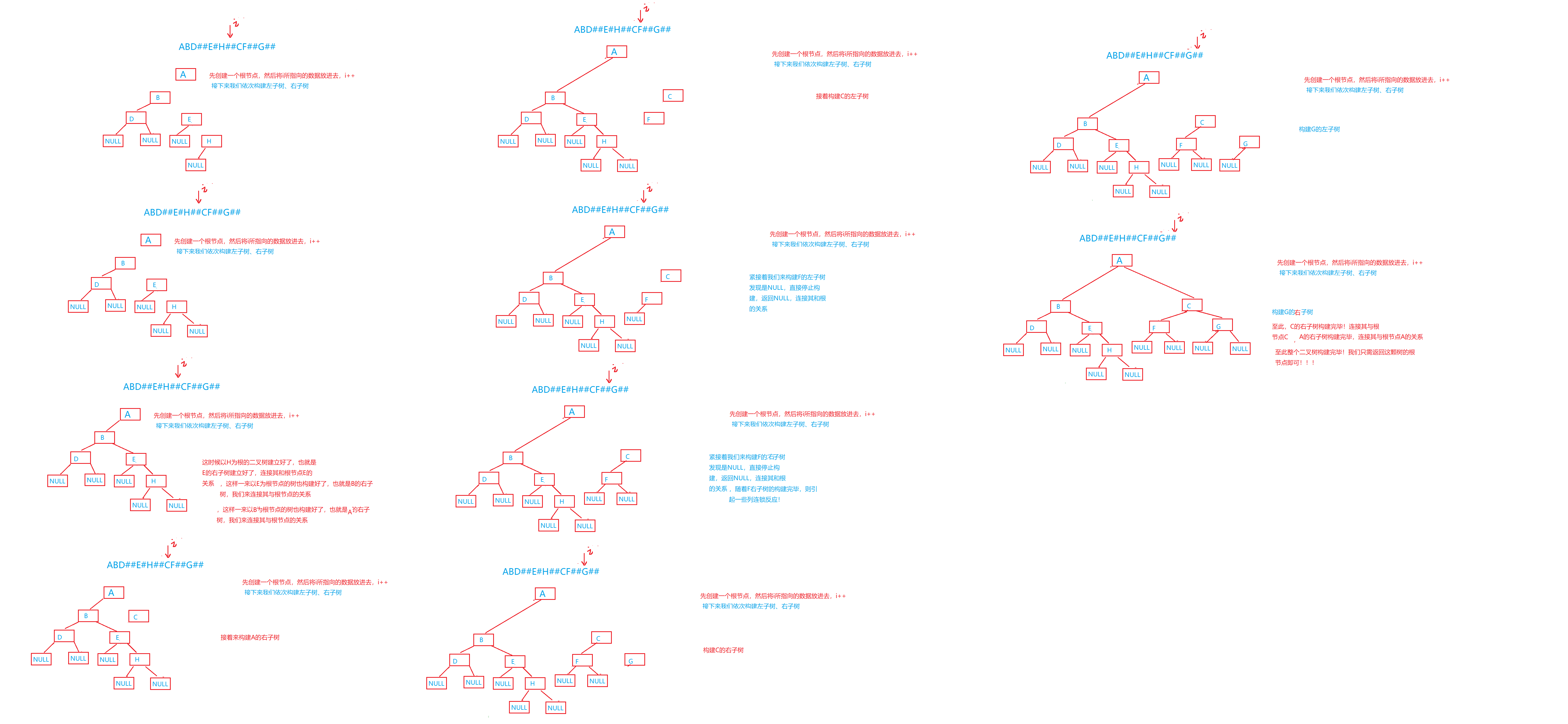
代码实现：

BTNode* BuyBTNode(BTDataType x)
{
	BTNode* ret = (BTNode*)malloc(sizeof(BTNode));
	if (!ret)
		exit(EXIT_FAILURE);
	ret->val = x;
	ret->left = NULL;
	ret->right = NULL;
	return ret;
}
BTNode* BinaryTreeCreate(BTDataType* a,int* pi)
{
	if (a[*pi]=='#')
	{
		*pi += 1;
		return NULL;
	}
	BTNode* root = BuyBTNode(a[*pi]);
	*pi += 1;
	root->left=BinaryTreeCreate(a, pi);//构建左子树；
	root->right=BinaryTreeCreate(a,pi);//构建右子树
	return root;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

当然利用中序、后序遍历建立二叉树也是同样的道理！

相关题目连接：题目链接

销毁二叉树

刚才我们利用前序遍历的方法建立了一个二叉树，我们建立了，不用了就得销毁啊！
为此销毁也是分3种方式！
1、利用前序遍历销毁：根、左子树、右子树
只不过我们需要注意，我们是先销毁的根，为了避免根被销毁过后找不到左子树、右子树，我们需要先保留一下左子树的根节点和右子树的根节点!

void PrevDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTNode* Left = root->left;//
	BTNode* Right = root->right;//需要提前保存避免找不到左右子树
	free(root);
	PrevDestroy(Left);//销毁左子树
	PrevDestroy(Right);//销毁右子树
}

void BinaryTreeDestory(BTNode** root)
{
	BTNode* head = *root;
	PrevDestroy(head);
	*root = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

2、利用中序遍历销毁二叉树：左子树、根、右子树

//利用中序销毁二叉树
void InDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTNode* Left = root->left;//
	BTNode* Right = root->right;//需要提前保存避免找不到左右子树
	InDestroy(Left);//先销毁左子树
	free(root);
	InDestroy(Right);//在销毁右子树
}
void BinaryTreeDestory(BTNode** root)
{
	BTNode* head = *root;
	InDestroy(head);
	*root = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

3、利用后序遍历销毁二叉树：左子树、右子树、根
这时候我们就可以不用保存左右子树的根节点了，因为我们是最后才销毁根节点，可以放心的删除！

//利用后序销毁二叉树
void PostDestroy(BTNode* root)
{
	if (root == NULL)
		return;
	BTNode* Left = root->left;//
	BTNode* Right = root->right;//
	PostDestroy(Right);//先销毁右子树
	PostDestroy(Left);//在销毁左子树
	free(root);
}
void BinaryTreeDestory(BTNode** root)
{
	BTNode* head = *root;
	PostDestroy(head);
	*root = NULL;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17

当然我们还可以利用层序遍历来销毁二叉树，这里就不写了，读者可以自己写一下！

总结

当然以上便是二叉树的一些常见操作；
如果向进一步加强对于二叉树和递归的理解；
建议刷一刷下面的题：

1. 单值二叉树。Oj链接
2. 检查两颗树是否相同。OJ链接
3. 对称二叉树。OJ链接
4. 二叉树的前序遍历。 OJ链接
5. 二叉树中序遍历 。OJ链接
6. 二叉树的后序遍历 。OJ链接
7. 另一颗树的子树。OJ链接