数学建模学习之主成分分析与因子分析_主成分pc1和pc2占比的意义

数学建模学习 day01

主成分分析与因子分析

常用的降维方法

具体的方法可以自行搜索或者阅读 ‘‘西瓜书’’,这里便不详细展开了

正文:主成分分析(PrincipalComponentAnalysis,简称PCA)

对于正交属性空间中的样本点，如何用一个超平面对所有样本进行恰当的表达？
容易想到，若存在这样的超平面，那么它大概应具有这样的性质：

• 最近重构性：样本点到这个超平面的距离都足够近；
• 最大可分性：样本点在这个超平面上的投影能尽可能分开。
  基于最近重构性和最大可分性，能分别得到主成分分析的两种等价推导

光看概念的话也许半懂不懂,我们结合抽象的例子来理解一下什么是主成分分析
注:下图来自简书

主成分分析的抽象理解

如下图所示，样本有2个特征(特征1,特征2)
现在我们需要对该样本进行降维处理
首先考虑的方法是直接降维(也就是简单粗暴的删除一个特征)
如,直接选择特征1或者特征2降维，经过降维后的样本由2维降到1维，如图所示

下图为只保留特征2

下图为只保留特征1

可以看出剔除特征2降维比剔除特征1降维的样本间的间距更大，即样本可区分度更大。
那么是否还有其他的映射方式，使得映射后样本的间距更大，事实上还可以选择某个轴线，例如下图所示，样本映射到该轴线之后，有更大的间距。

 PCA降维的思想就是寻找某个轴线，使得样本映射到该轴线上后使得样本区分度更大。
结合上图再想想之前所提到的两个概念是不是清晰了许多

• 最近重构性：样本点到这个超平面的距离都足够近；
• 最大可分性：样本点在这个超平面上的投影能尽可能分开。
  接下里的问题就是如何得到这个轴线
  (注意,为了方便举例画图说明,所以举的例子大多数都是二维的,但是PCA降维不仅仅局限于这么低的维度)

PCA降维步骤

下图是一组二维的数据

步骤一:中心化

$\sum x_i=0$
先求出数据的均值,再把均值的点移到圆心的位置
我们可以理解为每个数据减去均值

步骤二:找最优拟合直线PC1

重新选择投影方向: 方差最大

• 计算方法1 : 投影点到均值距离最大
• 计算方法2: 等价于点到直线距离最小
  最后得出了最优解
  
  下图是我们计算后得出的最优只写(具体的计算过程代码已经封装好,详细的推导这里暂不介绍)
  比方说我们得到的最优直线的斜率为0.25
  那么这个0.25可以看作 Gene1轴的影响力与Gene2轴的影响力之比 = 4:1
  这种也叫线性组合
  

步骤三:找最优拟合直线PC2

之前我们找到的PC1是第一个主成分,现在来分析第二个主成分,因为我们之前的数据是二维数据,所以只需要两个主成分之间线性无关即可,也就是第二个主成分PC2 垂直于PC1

步骤四:坐标变换

这一步没什么好说的

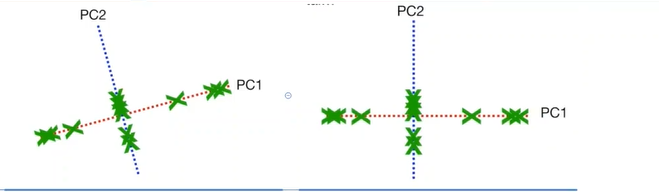
步骤5:方差之比的计算

之前的二维数据,得到的两个主成分之间,我们计算出他们各自的方差和
PC1 = 15
**PC2 = 3 **
所以PC1所占的比为83% PC2为17%
这里的方差代表的信息量的大小,我们的目标就是在降维的同时保留尽可能多的数据

比如我们可以删除纵向的轴,来保留横向的PC1,这样就保留了83%的信息

有时候,我们对保留的信息量有自己的要求,这在高维数据中体现的更多
比如对一个三维的数据我们经过PCA之后得出了PC1,PC2,PC3
如果我们最后想保留90%以上的信息量,就需要保留PC1,PC2维度的信息,可以删除PC3的信息

正文:因子分析

因子分析是指研究从变量群中提取共性因子的统计技术。最早由英国心理学家C.E.斯皮尔曼提出。他发现学生的各科成绩之间存在着一定的相关性，一科成绩好的学生，往往其他各科成绩也比较好，从而推想是否存在某些潜在的共性因子，或称某些一般智力条件影响着学生的学习成绩。因子分析可在许多变量中找出隐藏的具有代表性的因子。将相同本质的变量归入一个因子，可减少变量的数目，还可检验变量间关系的假设。
——《百度百科–因子分析》
友情链接:因子分析概念详解

什么是因子分析

因子分析的步骤

1.根据问题选取原始变量;
2. 求其相关阵R，探讨其相关性;
3.从R求解初始公共因子F及因子载荷矩阵A(主成分法);
4.因子旋转， 分析因子的含义;
5.计算因子得分函数;
6.根据因子得分值进行进一步分析(例如综合评价)

因子分析与主成分分析的区别与联系：

1.因子分析、主成分分析都是重要的降维方法(数据简化技术)， 因子分析可以看作是主成分分析的推广和发展。
2.主成分分析不能作为一个模型来描述， 它只能作为一般的变量变换，主成分是可观测的原始变量的线性组合; 因子分析需要构造因子模型，公共因子是潜在的不可观测的变量，一般不能表示为原始变量的线性组合。
3.因子分析是用潜在的不可观测的变量和随机影响变量的线性组合来表示原始变量，即通过这样的分解来分析原始变量的协方差结构(相依关系)