pytorch学习——多层感知机_利用pytnon探究多层感知机数据集大小隐含层层数隐含层节点数影响因素实验报告

一.感知机

        感知机——神经网络基本单元，最简单的深度网络称为多层感知机。多层感知机由多层神经元组成，每一层与它上一层相连，从中接收输入， 同时每一层也与它的下一层相连，影响当前层的神经元。

 

 解释：如果正确分类，-y<W,X>小于0，即该分类点对应的损失函数的值为0；如果错误分类，则-y<W,X>大于等于0，并进入梯度下降算法的计算。

 示例：以下图中猫狗分类为例，其中黑线表示区分猫和狗的轴

 当输入一直新的狗时，原来的线会导致分类错误，得更新

 

 收敛定理：什么时候能够停止？

 r指数据大小

感知机存在的问题：不能拟合异或问题——不能通过线性完成此问题的分类

 感知机的局限性就在于它只能表示由一条直线分割的空间。图8这样弯曲的曲线无法用感知机表示。另外，由下图这样的曲线分割而成的空间称为非线性空间。

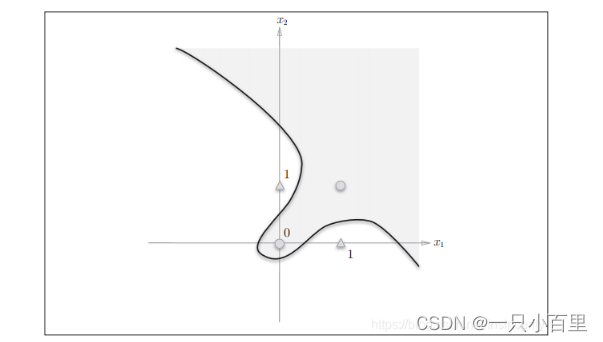
 总结：

1.感知机是一个二分类模型，是最早的AI模型之一

2.它的求解算法等价于使用批量大小为1的梯度下降

3.不能拟合异或函数（XOR）函数

二、感知机的实现

2.1简单感知机的实现

        先定义一个接收参数x1和x2的AND函数。（实现与门）

def AND(x1, x2):
	w1, w2, theta = 0.5, 0.5, 0.7
	tmp = x1*w1 + x2*w2
	if tmp <= theta:
		return 0
	elif tmp > theta:
		return 1

        在函数内初始化参数w1、 w2、 theta，当输入的加权总和超过阈值时返回1，否则返回0。我们来确认一下输出结果是否如图2 与门真值表所示。测试结果如下所示：

AND(0, 0) # 输出0
AND(1, 0) # 输出0
AND(0, 1) # 输出0
AND(1, 1) # 输出1

2.2导入权重和偏置

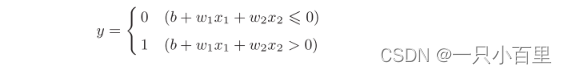
     b称为偏置， w1和w2称为权重

 实现与门

def AND(x1, x2):
	x = np.array([x1, x2])
	w = np.array([0.5, 0.5])
	b = -0.7
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1

类似，可以继续实现或门和非门

def NAND(x1, x2):
	x = np.array([x1, x2])
	w = np.array([-0.5, -0.5]) # 仅权重和偏置与AND不同！
	b = 0.7
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1
		
def OR(x1, x2):
	x = np.array([x1, x2])
	w = np.array([0.5, 0.5]) # 仅权重和偏置与AND不同！
	b = -0.2
	tmp = np.sum(w*x) + b
	if tmp <= 0:
		return 0
	else:
		return 1

三.多层感知机

        可以解决单层感知机不能实现异或的问题，例如，可以通过蓝色线分类的结果乘以黄色线分类结果来实现异或

 

 输入输出都是固定的，唯一能做的就是设置隐藏层大小

 这个多层感知机有4个输入，3个输出，其隐藏层包含5个隐藏单元。 输入层不涉及任何计算，因此使用此网络产生输出只需要实现隐藏层和输出层的计算。 因此，这个多层感知机中的层数为2。 注意，这两个层都是全连接的。 每个输入都会影响隐藏层中的每个神经元， 而隐藏层中的每个神经元又会影响输出层中的每个神经元。

 因为不加非线性层的话，输出还是线性函数（仍然不能解决XOR），还是相当于单层

四.激活函数

        激活函数（activation function）通过计算加权和并加上偏置来确定神经元是否应该被激活， 它们将输入信号转换为输出的可微运算。 大多数激活函数都是非线性的。 由于激活函数是深度学习的基础，下面简要介绍一些常见的激活函数。

4.1Relu函数

 

x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))

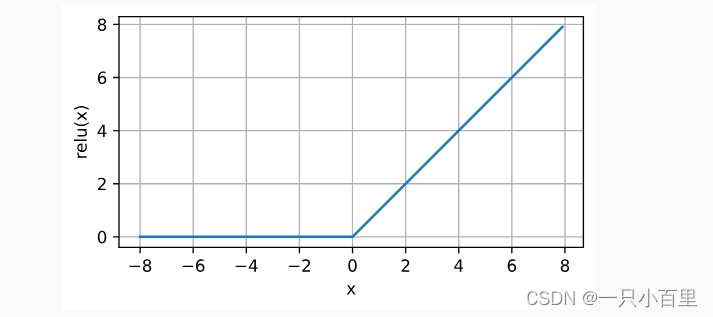
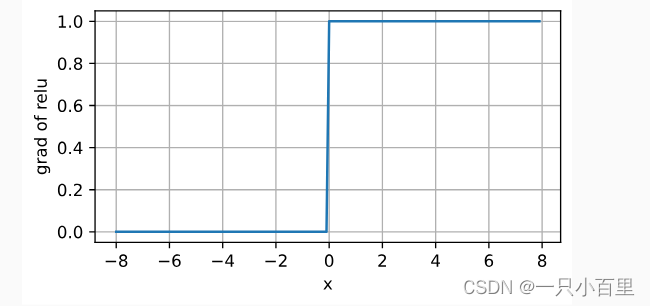
         当输入为负时，ReLU函数的导数为0，而当输入为正时，ReLU函数的导数为1。 注意，当输入值精确等于0时，ReLU函数不可导。 在此时，我们默认使用左侧的导数，即当输入为0时导数为0。 我们可以忽略这种情况，因为输入可能永远都不会是0。  下面我们绘制ReLU函数的导数。

y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))

 4.2sigmoid函数

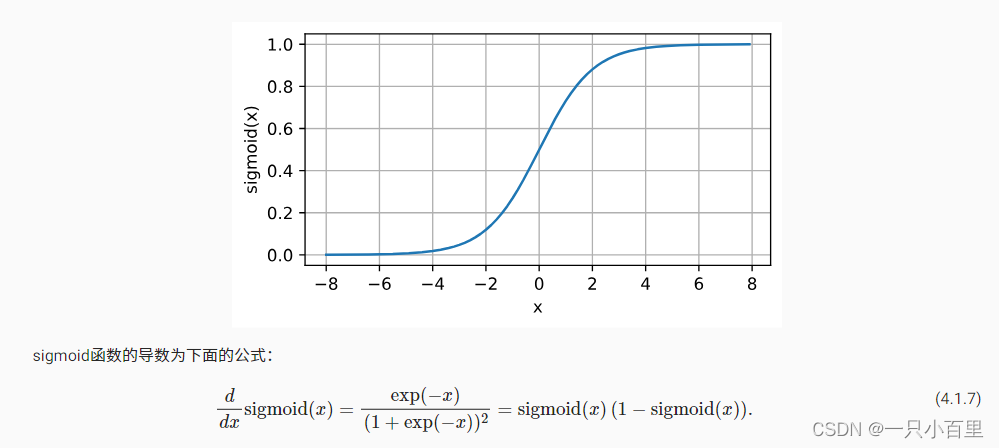
 下面，我们绘制sigmoid函数。 注意，当输入接近0时，sigmoid函数接近线性变换。

y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))

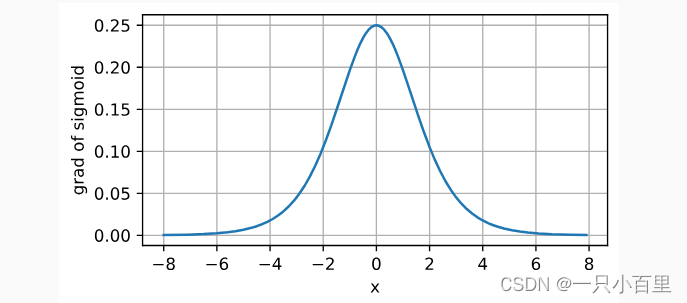
 sigmoid函数的导数图像如下所示。 注意，当输入为0时，sigmoid函数的导数达到最大值0.25； 而输入在任一方向上越远离0点时，导数越接近0。

# 清除以前的梯度
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))

多层感知机和softmax的区别就是加一个非线性层 

 五.总结

1.多层感知机使用隐藏层和激活函数来得到非线性模型

2.常用激活函数——sigmoid，Relu，Tanh

3.使用softmax来处理多类分类

4.超参数为隐藏层数，和各个隐藏层的大小