热门标签
热门文章
- 1用 NodeJS 10分钟快速实现基于 ChatGPT 的简历智能解析 Agent_nodejs llm
- 2gcc中的环境变量_gcc环境变量
- 3Android系统Framework定制默认值预置修改
- 4thingsboard3.2导入测试数据失败_thingsboard db installation failed!
- 5十部值得一看的电影
- 6PHP调用API接口的方法及实现_php测试api接口
- 7迁移学习相关资料_transformer 迁移 王晋东
- 8tp中如何防止mysql注入_ThinkPHP5漏洞分析之SQL注入(一)
- 9C++控制台光标控制与进度条绘制_c++进度条
- 10MyBatis动态SQL中if、where、trim、choose、when、otherwise、foreach标签及sql标签范例_mybatis otherwise
当前位置: article > 正文
Leetcode:96. 不同的二叉搜索树(C++)
作者:Monodyee | 2024-03-08 11:20:59
赞
踩
Leetcode:96. 不同的二叉搜索树(C++)
目录
问题描述:
给你一个整数 n ,求恰由 n 个节点组成且节点值从 1 到 n 互不相同的 二叉搜索树 有多少种?返回满足题意的二叉搜索树的种数。
示例 1:
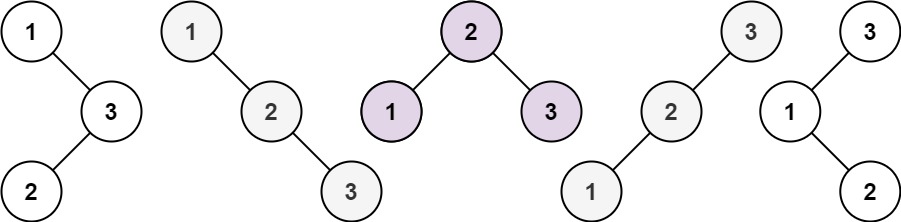
输入:n = 3 输出:5
示例 2:
输入:n = 1 输出:1
实现代码与解析:
动态规划:
- class Solution {
- public:
- int numTrees(int n)
- {
- vector<int> dp(n+1,0);
- dp[0] = 1;
- dp[1] = 1;
- for(int i = 2; i < n + 1; i++)
- {
- for(int j = 1; j < i + 1; j++)
- {
- dp[i] += dp[i - j] * dp[j - 1];//各种情况加起来
- }
- }
- return dp[n];
- }
- };

原理思路:
代码很好写,但是用动态规划来解题其实是很难想到的,而且动态规划的递推公式也不太容易找出,如果没有提前写过,其实是很难做出来的。
主要讲讲递推公式怎么来的,首先dp数组就是表示 i 个结点的二叉搜索树的种树,头节点为 1 ~ i 的树,因为头结点已经占了一个结点,我们就把 i - 1 的结点分割在左右子树上,左右子树当然也有不同种类但结点个数相同的树,所以一种分割方式求出来的结果是相乘求出来的,最后不同分割方式相加就得到了最终结果。
其实仅仅文字这样解释依旧还是挺难想到和理解到的,画了个图,大家可以理解一下,注意不要在意结点里的值,只要符合二叉搜索树的规则就行,这里的种类仅仅是指的结构,结点值不同但结构相同的是一种。
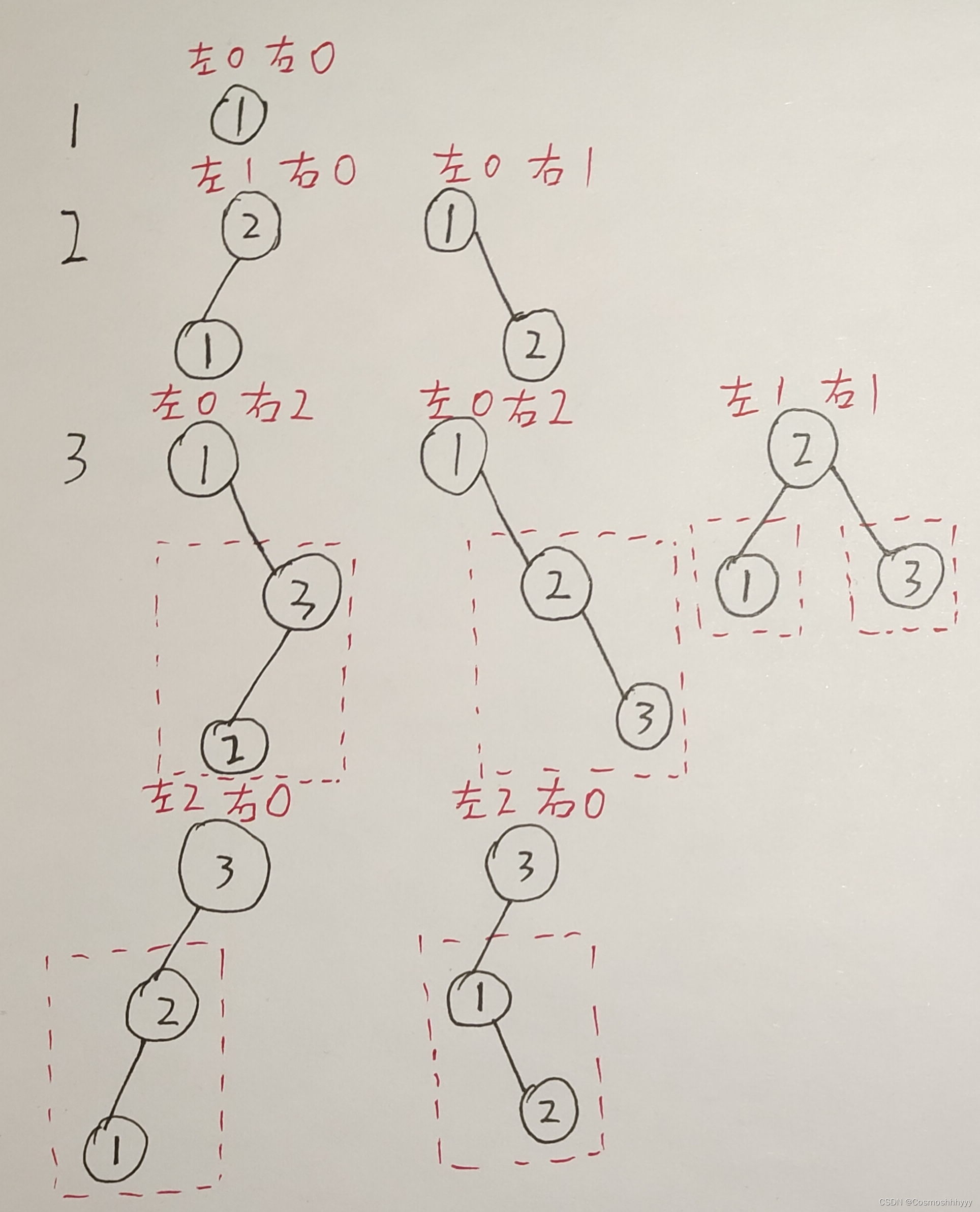
大家可以发现画红框的是不是就是我们已经推导过的种类啊,用代码写出就是:
dp[i] += dp[i - j] * dp[j - 1];//各种情况加起来大家可以带入数字验证,顺便再次理解一下。
数学法:
- class Solution {
- public:
- int numTrees(int n) {
- long long C = 1;
- for (int i = 0; i < n; ++i)
- {
- C = C * 2 * (2 * i + 1) / (i + 2);
- }
- return (int)C;
- }
- };
-
原理思路:
用的数学中的卡塔兰数,大家可以自己网上查一下。
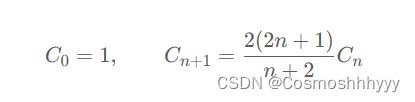
声明:本文内容由网友自发贡献,版权归原作者所有,本站不承担相应法律责任。如您发现有侵权的内容,请联系我们。转载请注明出处:【wpsshop博客】
推荐阅读
相关标签


