【数字信号处理】定点数的表示之二进制数的原码与补码_数字信号如何用二进制表示

作者：Li_阴宅 | 2024-08-16 03:32:45

踩

数字信号如何用二进制表示

为什么要讲这个简单的问题，就是因为看到了一些比较玄乎的表达方式，归根到底也能得到二进制的原码和补码表示，但就是看着难受，为此，为了让自己不被同化，记录下最简单的求二进制原码和补码的方式。

数字信号处理涉及大量的数学运算，既然是数学运算，就涉及一个根本的问题，数字的表示方法。

数字的表示方法分为定点数的表示和浮点数的表示。就FPGA而言，其胜任定点运算的能力更为显著。

定点数所涉及的内容之一，就是二进制数的表示，因为计算机都是以二进制数表示数字，所以对这方面深入理解还是很有必要的。

对于无符号数而言，使用二进制数的原码来表示；

对于有符号数而言，则使用二进制数的补码来表示。

如何求解有符号数的补码呢？

规则是，正数的原码和补码一致，负数的补码是原码的符号位不变，其他位取反加1（或直接取绝对值，之后求反加1）.

N为二进制数能表示的无符号整数范围是 $\left [ 0,2^{N}-1 \right ]$ ，所能表示的有符号整数范围是 $[-2^{N-1},2^{N-1}-1]$ .

我们不妨试一下，以4位二进制数为例:

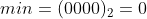
表示无符号数时，最大数 $max=(1111)_{2}=(2^4-1)_{10}=15$ , $min=(0000)_{2}=0$

表示有符号数时，由于我们采用的是补码的形式，所以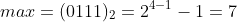 $max=(0111)_{2}=2^{4-1}-1=7$ ,

$min=(1000)_{2}=-8$

这个最小值，我需要提出来讲，因为它比较难以理解。

我们列一个表格，来看看4位二进制有符号整数的补码和原码表示：

从这张表中可以看出，-8不存在原码，那-8的补码是怎么求的呢？或者-8的补码有什么来历？

根据前面的规则：

对于无符号数而言，使用二进制数的原码来表示；

对于有符号数而言，则使用二进制数的补码来表示。

如何求解有符号数的补码呢？

规则是，正数的原码和补码一致，负数的补码是原码的符号位不变，其他位取反加1.

求解负数的补码，一般而言，我们需要得到该数的原码，然后根据规则来求补码，可是我们看到，-8根本就不存在原码，如何有补码呢？

这里是一个规定，规定-8的补码是1000。

别急，我们这里说说来历：

先说说原码的缺陷，为什么有符号数不用原码来表示呢？非要搞出一个补码来？

对于有符号数而言，0的表示有两种：+0和-0，二者是相等的，都是0，如果用原码来表示0，如何表示呢？（以4位2进制数为例）

+0 => 0000

-0 => 1000

这就麻烦了，0有两种表示方法，所以呢？这就是原码表示有符号数的缺陷，我们取0的原码表示为0000，剩下一个1000没用到，后面有用。

既然原码有缺陷，我们设计了补码的表示方法，并设计了求补码的规则，上面已经说了好几遍了。

从-1到-7都可以用这个规则来求解补码，就是-8由于没有原码，无法使用规则求解，这里就将-0的原码1000作为-8的补码表示。

这样，从-1到-8都有相应的二进制码表示了，岂不快哉！

下面的一个话题是符号位扩展：

我们都知道-4的补码表示是1100，这是用4为二进制数表示的，如果我要求用5位二进制数表示，我们同样使用规则来求：

-4的原码是10100，之后符号位不变，其他位取反加1，得到11100.

可见，11100是将1100的符号位扩展1位得到的。

所谓的符号位扩展，是指将符号位向高位复制。这说明符号位扩展是不改变数值大小的。

最后一个话题：

有符号数X补码表示的最小位宽，直接给出公式：

$w_{s}=ceil[log_{2}( \left | X \right | + 1 )]+1$

对于无符号整数，因为不需要符号位，所以二进制原码表示时的最小位宽为：

$w_{s}=ceil[log_{2}(X + 1 )]$

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Li_阴宅/article/detail/986477

【 数字信号处理 】定点数的表示之二进制数的原码与补码_数字信号如何用二进制表示