深度学习二 —— 手撕激活函数(阶跃函数、sigmoid、tanh、ReLu、Leaky ReLu)_深度学习经典公式sigmod与tanh

手撕激活函数

1. 阶跃函数

公式

$$step(x)=\{\begin{array}{l}1ifx>0\\ 0ifx\le 0\end{array}$$

代码

import numpy as np
def step_function(x):
    return np.array(x > 0, dtype=np.int)
1
2
3

2. sigmoid

公式

$$sigmoid(x)=\frac{1}{1+e^{-x}}$$

y的取值范围 $(0,1)$

代码

import numpy as np
def sigmoid(x):
    return 1. / (1 + np.exp(-x))
1
2
3

3. 阶跃函数 与 sigmoid函数比较

相同点

• 输入小的时候，输出接近0，或者为0；随着输入增大，输出会向1靠近，或者为1
• 不管输入信号的大小，输出均在$[0,1]$

不同点

• 平滑性不同，sigmoid可以返回$[0,1]$之间的所有实数，阶跃函数只能返回0或1的信号值。
• 由上可知，感知机中神经元之间流动的是0或1的信号值，而神经网络之间流动的是连续的实数值信号。

4. tanh 函数

公式

$$tanh(x)=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

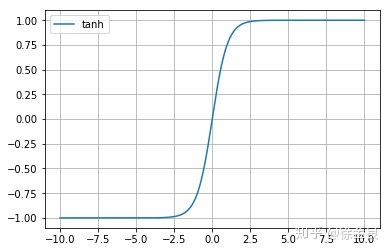
代码

import numpy as np
def tanh(x):
    return (np.exp(x) - np.exp(-x)) / (np.exp(x) + np.exp(-x))
1
2
3

5. sigmoid 和 tanh的缺陷

sigmoid和tanh具有共同的缺陷，即：在x很大或者很小时，梯度几乎为0，因此使用梯度下降的优化算法更新网络会很慢。

也正因为这个缺陷，ReLu成为目前大多数神经网络的默认选择。

6. ReLu 函数

公式

$$ReLu(x)=\{\begin{array}{l}xifx>0\\ 0ifx\le 0\end{array}$$

代码

import numpy as np
def relu(x):
    return np.maximum(0, x)
1
2
3

ReLu的缺点

ReLu的缺点：当$x<0$时，斜率即导数为0，因此引申出leaky relu函数，但是实际上leaky relu使用的并不多。

7. leaky ReLu 函数

公式

$$LReLu(x)=\{\begin{array}{l}0.01xifx<0\\ xifx\le 0\end{array}$$

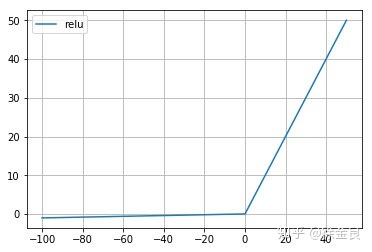
代码

import numpy as np
def LReLu(x):
    return maximum(0.01 * x, x)
1
2
3