三角函数和解三角形的考向收集整理【三轮总结】

一、考查三角函数的基本变换

• 此时最常用的公式为二倍角的正弦、余弦公式的逆用，辅助角公式，转化化归为正弦型$f(x)=Asin(\omega x+\phi)+k$

例1 已知函数$f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1$ $f(x)=sin2x+\sqrt{3}(2cos^2x-1)+1$ $=sin2x+\sqrt{3}cos2x+1$ $=2sin(2x+\cfrac{\pi}{3})+1$ 解后反思： 1、熟练掌握这样的变形是非常必要的。 2、当然，此时还可能有一个变形方向，即转化为二次型。比如某个题目可以转化为$f(x)=(sinx-1)^2+2$，当然这样的变形后，下一步能考查的方向很窄。

二、考查三角函数的基本性质

• 此时常常类比模板函数$f(x)=sinx$的性质求解正弦型$f(x)=Asin(\omega x+\phi)+k$的性质

例2 已知函数$f(x)=2sinx\cdot cosx+2\sqrt{3}\cdot cos^2x-\sqrt{3}+1=2sin(2x+\cfrac{\pi}{3})+1$ * 考向：求周期； 由$T=\cfrac{2\pi}{2}$，得到$T=\pi$ * 考向：求值域$(x\in R 或 x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}])$；最值(和最值点)； 若$x\in R$，则 当$sin(2x+\cfrac{\pi}{3})=1$时，即$2x+\cfrac{\pi}{3}=2k\pi+\cfrac{\pi}{2}(k\in Z)$，即$x=k\pi+\cfrac{\pi}{12}(k\in Z)$时，$f(x)_{max}=2\times1+1=3$； 当$sin(2x+\cfrac{\pi}{3})=-1$时，即$2x+\cfrac{\pi}{3}=2k\pi-\cfrac{\pi}{2}(k\in Z)$，即$x=k\pi-\cfrac{5\pi}{12}(k\in Z)$时，$f(x)_{max}=2\times(-1)+1=-1$； 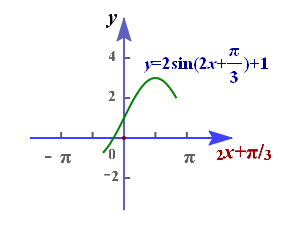若$x\in [-\cfrac{\pi}{3}，\cfrac{\pi}{4}]$，则可得 $-\cfrac{2\pi}{3}\leq 2x\leq \cfrac{\pi}{2}$，则$-\cfrac{\pi}{3}\leq 2x+\cfrac{\pi}{3}\leq \cfrac{5\pi}{6}$， 故当$2x+\cfrac{\pi}{3}=-\cfrac{\pi}{3}$，即$x=-\cfrac{\pi}{3}$时，$f(x)_{min}=f(-\cfrac{\pi}{3})=2\times (-\cfrac{\sqrt{3}}{2})+1=-\sqrt{3}+1$； 故当$2x+\cfrac{\pi}{3}=\cfrac{\pi}{2}$，即$x=\cfrac{\pi}{12}$时，$f(x)_{max}=f(\cfrac{\pi}{12})=2\times 1+1=3$； * 考向：求函数$f(x)$对称轴方程和对称中心坐标； 令$2x+\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}(k\in Z)$，得到$f(x)$对称轴方程为$x=\cfrac{k\pi}{2}+\cfrac{\pi}{12}(k\in Z)$； 令$2x+\cfrac{\pi}{3}=k\pi(k\in Z)$，得到$f(x)$的对称中心坐标为$(\cfrac{k\pi}{2}-\cfrac{\pi}{6}，1)(k\in Z)$ * 考向：求奇偶性$\left(奇函数利用f(0)=0；偶函数利用f(0)=f(x)_{max}或f(x)_{min}\right)$ 比如，函数$g(x)=2sin(2x+\phi+\cfrac{\pi}{3})(\phi\in (0，\pi))$是偶函数，求$\phi$的值。 分析：由于函数$g(x)$是偶函数，则在$x=0$处必然取到最值， 故有$2\times 0+\phi+\cfrac{\pi}{3}=k\pi+\cfrac{\pi}{2}(k\in Z)$， 则$\phi=k\pi+\cfrac{\pi}{6}(k\in Z)$ 令$k=0$，则$\phi=\cfrac{\pi}{6}\in (0，\pi)$，满足题意，故所求$\phi=\cfrac{\pi}{6}$时，函数$g(x)$是偶函数。 解后反思： 1、当然，求值域还可能有这样的变形，即转化为二次型。 高考题(2017高考真题 理科全国卷2的第14题) 函数$f(x)=sin^2x+\sqrt{3}cosx-\cfrac{3}{4}(x\in[0，\cfrac{\pi}{2}])$的最大值为_______。 分析：由于$x\in[0，\cfrac{\pi}{2}]$，则$cosx\in [0，1]$， 令$cosx=t\in [0，1]$，$f(x)=1-cos^2x+\sqrt{3}cosx-\cfrac{3}{4}=1-t^2+\sqrt{3}t-\cfrac{3}{4}=-(t-\cfrac{\sqrt{3}}{2})^2+1=g(t)$， 故当$t=\cfrac{\sqrt{3}}{2}$时，$g(t)_{max}=f(x)_{max}=1$。

三、考查常用的三角变换和解三角形(求角或求边)

• 此时最常用的公式有三角形中的诱导公式、正弦定理、余弦定理，方程理论

例3(2017高考真题 理科全国卷2的第17题) $\Delta ABC$ 的内角$A，B，C$的对边分别是$a，b，c$，已知$sin(A+C)=8sin^2\cfrac{B}{2}$。 (1)求$cosB$. 分析：$sin(A+C)=sinB=8\cdot \cfrac{1-cosB}{2}$，得到$sinB=4(1-cosB)$， 即$\sqrt{1-cos^2B}=4(1-cosB)$，平方得到$17cos^2B-32cosB+15=0$。 由十字相乘法得到 $(17cosB-15)(cosB-1)=0$， 得到$cosB=\cfrac{15}{17}$或$cosB=1(舍去)$，故$cosB=\cfrac{15}{17}$； (2)若$a+c=6$，$S_{\Delta ABC}=2$，求$b$. 分析：由$cosB=\cfrac{15}{17}$得到$sinB=\cfrac{8}{17}$， 由$S_{\Delta ABC}=\cfrac{1}{2}acsinB=2$得到，$ac=\cfrac{17}{2}$， 故$b^2=a^2+c^2-2accosB=(a+c)^2-2ac-2accosB=6^2-2\cdot \cfrac{17}{2}-2\cdot \cfrac{17}{2}\cdot\cfrac{15}{17}=4$， 故$b=2$。

四、考查常用的三角变换和三角函数的单调性

• 此时最常用的公式为二倍角的正弦、余弦公式的逆用，辅助角公式，以及整体思想和赋值法；2018年首次出现和导数结合的题型。

例4(2016.天津高考) 已知函数$f(x)=4tanx\cdot sin(\cfrac{\pi}{2}-x)\cdot cos(x-\cfrac{\pi}{3})-\sqrt{3}$， 试讨论$f(x)$在区间$[-\cfrac{\pi}{4}，\cfrac{\pi}{4}]$上的单调性。 解析：先将所给函数化简为正弦型或者余弦型， $f(x)=4tan\cdot cosx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}$ $=4sinx(cosx\cdot \cfrac{1}{2}+sinx\cdot \cfrac{\sqrt{3}}{2})-\sqrt{3}=2sinxcosx+2\sqrt{3}sin^2x-\sqrt{3}$ $=sin2x+\sqrt{3}(1-cos2x)-\sqrt{3}=sin2x-\sqrt{3}cos2x$ $=2sin(2x-\cfrac{\pi}{3})$ 法1：先求解函数在$x\in R$上的单调区间， 令$2k\pi-\cfrac{\pi}{2}\leq 2x-\cfrac{\pi}{3}\leq 2k\pi+\cfrac{\pi}{2}(k\in Z)$， 得到单调递增区间为$[k\pi-\cfrac{\pi}{12}，k\pi+\cfrac{5\pi}{12}](k\in Z)$， 又因为$x\in [-\cfrac{\pi}{4}，\cfrac{\pi}{4}]$ 然后给$k$赋值，令$k=0$， 得到函数在区间$[-\cfrac{\pi}{12}，\cfrac{\pi}{4}]$上单调递增，在区间$[-\cfrac{\pi}{4}，-\cfrac{\pi}{12}]$上单调递减。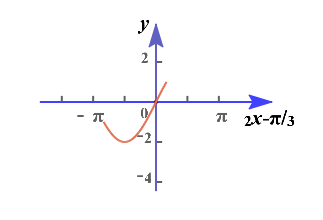 法2：由$-\cfrac{\pi}{4}\leq x\leq \cfrac{\pi}{4}$，求得$-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}$， 结合横轴为$2x-\cfrac{\pi}{3}$的图像可知， 当$-\cfrac{5\pi}{6}\leq 2x-\cfrac{\pi}{3}\leq -\cfrac{\pi}{2}$时，求得函数在区间$[-\cfrac{\pi}{4}，-\cfrac{\pi}{12}]$单调递减； 当$-\cfrac{\pi}{2}\leq 2x-\cfrac{\pi}{3}\leq \cfrac{\pi}{6}$时，求得函数在区间$[-\cfrac{\pi}{12}，\cfrac{\pi}{4}]$单调递增； 例5+新考向【2018高考一卷第16题】
求$f(x)=2sinx+sin2x$的最小值。【最值和导数相结合的题型】
法1：$f'(x)=2cosx+2cos2x=2cosx+2(2cos^2x-1)$
$=4cos^2x+2cosx-2=(2cosx+2)(2cosx-1)$
$=4(cosx+1)(cosx-\cfrac{1}{2})$
注意到$cosx+1\ge 0$恒成立，故
令$f'(x)>0$得到，$cosx>\cfrac{1}{2}$，令$f'(x)<0$得到，$cosx 则$x\in [2k\pi-\cfrac{5\pi}{3}，2k\pi-\cfrac{\pi}{3}](k\in Z)$时，函数$f(x)$单调递减；
$x\in [2k\pi-\cfrac{\pi}{3}，2k\pi+\cfrac{\pi}{3}](k\in Z)$时，函数$f(x)$单调递增；
故当$x=2k\pi-\cfrac{\pi}{3}(k\in Z)$时，$f(x)_{min}=f(2k\pi-\cfrac{\pi}{3})=-\cfrac{3\sqrt{3}}{2}$。

五、考查三角形的周长和面积

• 此时往往已经知道三角形的一条边和其对角，使用面积公式求面积，由余弦定理求得另外两边长之和，从而求得周长。

例6(2017$\cdot$全国卷I) 已知$\Delta ABC$的内角$A，B，C$的对边分别是$a，b，c$，$S_{\Delta ABC}=\cfrac{a^2}{3sinA}$； (1)求$sinBsinC$的值； (2)若$6cosBcosC=1$，$a=3$，求$\Delta ABC$的周长； 分析：(1)由$S_{\Delta ABC}=\cfrac{1}{2}acsinB=\cfrac{a^2}{3sinA}$， 变形得到$\cfrac{1}{2}csinB=\cfrac{a}{3sinA}$， 边化角，得到$\cfrac{1}{2}sinCsinB=\cfrac{sinA}{3sinA}$， 故$sinBsinC=\cfrac{2}{3}$。 (2)由于求三角形周长的题目，一般都会知道一条边和其对角，现在知道了边$a$，故猜想应该能求得$A$， 这样想，我们一般就会将条件作差而不是作商， 由$cosBcosC-sinBsinC=-\cfrac{1}{2}$， 即$cos(B+C)=-cosA=-\cfrac{1}{2}$，得到$A=\cfrac{\pi}{3}$； 由题意$\cfrac{1}{2}bcsinA=\cfrac{a^2}{3sinA}$，$a=3$ 得到$bc=8$； 再由余弦定理得到$a^2=b^2+c^2-2bccosA$， 得到$3^2=(b+c)^2-2bc-2bccosA$，即$b+c=\sqrt{33}$； 故周长为$3+\sqrt{33}$。

六、考查三角形的面积的最大值，或某一边的最小值

• 此时往往可以利用均值不等式求最值或者利用三角函数求最值

例7【三轮模拟考试理科用题】 在$\Delta ABC$中，已知$4cos^2\cfrac{A}{2}-cos2(B+C)=\cfrac{7}{2}，a=2$，则$\Delta ABC$的面积的最大值为________. 分析：由$cos2(B+C)=cos(2B+2C)=cos(2\pi-2A)=cos2A$， 将已知等式变形为$2\cdot 2cos^2\cfrac{A}{2}-cos2A=\cfrac{7}{2}$， 即$2(1+cosA)-cos2A=\cfrac{7}{2}$， 即$2(1+cosA)-(2cos^2A-1)=\cfrac{7}{2}$， 化简为$4cos^2A-4cosA+1=(2cosA-1)^2=0$， 解得$cosA=\cfrac{1}{2}，A\in(0，\pi)$，故$A=\cfrac{\pi}{3}$， 到此题目转化为已知$A=\cfrac{\pi}{3}，a=2$，求$\Delta ABC$的面积的最大值。 接下来有两个思路途径： 思路一：使用均值不等式，由余弦定理$a^2=b^2+c^2-2bccosA，A=\cfrac{\pi}{3}，a=2$ 得到$b^2+c^2=4+bc\ge 2bc$，解得$bc\leq 4(当且仅当b=c=2时取到等号)$， 则$S_{\Delta ABC}=\cfrac{1}{2}bcsinA \leq \cfrac{\sqrt{3}}{4}\times 4=\sqrt{3}$。 即三角形面积的最大值是$\sqrt{3}$。 法2：由于题目已知$A=\cfrac{\pi}{3}，a=2$，则$B+C=\cfrac{2\pi}{3}$，故$B，C\in (0，\cfrac{2\pi}{3})$， 则由正弦定理得$\cfrac{b}{sinB}=\cfrac{c}{sinC} =\cfrac{a}{sinA} =\cfrac{2}{\frac{\sqrt{3}}{2}} =\cfrac{4\sqrt{3}}{3}$， 则$b=\cfrac{4\sqrt{3}}{3}sinB$，$c=\cfrac{4\sqrt{3}}{3}sinC$， 则$bc=(\cfrac{4\sqrt{3}}{3})^2\cdot sinB\cdot sinC=\cfrac{16}{3}sinB\cdot sin(\cfrac{2\pi}{3}-B)$ $=\cfrac{16}{3}sinB\cdot (\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)$ $=\cfrac{16}{3}[\cfrac{\sqrt{3}}{2}sinB\cdot cosB+\cfrac{1}{2}sin^2B]$ $=\cfrac{16}{3}[\cfrac{\sqrt{3}}{4}sin2B+\cfrac{1}{4}(1-cos2B)]$ $=\cfrac{16}{3}(\cfrac{\sqrt{3}}{4}sin2B-\cfrac{1}{4}cos2B+\cfrac{1}{4})$ $=\cfrac{8}{3}(sin2B\cdot \cfrac{\sqrt{3}}{2}-cos2B\cdot \cfrac{1}{2})+\cfrac{4}{3}$ $=\cfrac{8}{3}sin(2B-\cfrac{\pi}{6})+\cfrac{4}{3}$ 当$2B-\cfrac{\pi}{6}=\cfrac{\pi}{2}$，即$B=\cfrac{5\pi}{12} \in(0，\cfrac{2\pi}{3})$时，$sin(2B-\cfrac{\pi}{6})=1$， 即$bc_{max}=\cfrac{8}{3}+\cfrac{4}{3}=4$ 故$[S_{\Delta}]_{max}=\cfrac{1}{2}bcsinA\leq \cfrac{\sqrt{3}}{4}\times 4=\sqrt{3}$。 解后反思：求某边的最小值，比如已知$ac=4$，$B=\cfrac{\pi}{3}$， 则$b^2=a^2+c^2-2accosB=a^2+c^2-ac\ge 2ac-ac=ac=4$，即$b^2\ge 4$，即$b_{min}=2$

七、考查三角形的周长的最大值

• 此时常利用均值不等式或三角函数求最大值

例8【三角函数图像性质和解三角形结合】【2017•福州模拟】 在$\Delta ABC$中，角$A，B，C$的对边分别为$a，b，c$，满足$(2b-c)\cdot cosA=a\cdot cosC$。　 (1)求角$A$的大小；(考查角度：解三角形) (2)若$a=3$，求$\Delta ABC$的周长的最大值。(考查角度：三角函数图像性质) 分析：(1)由$(2b-c)\cdot cosA=a\cdot cosC$及正弦定理，边化角得到， 得$(2sinB-sinC)cosA=sinAcosC$， 所以$2sinBcosA=sinCcosA+sinAcosC$， 所以$2sinBcosA=sin(C+A)=sinB$， 因为$B\in (0，π)$，所以$sinB\neq 0$， 因为$A\in (0，π)$，$cosA=\cfrac{1}{2}$，所以$A=\cfrac{\pi}{3} $。 (2)由(1)得$A=\cfrac{\pi}{3} $， 由正弦定理得$\cfrac{b}{sinB}=\cfrac{c}{sinC} =\cfrac{a}{sinA} =\cfrac{3}{\frac{\sqrt{3}}{2}} =2\sqrt{3}$， 所以$b=2\sqrt{3}\cdot sinB$； $c=2\sqrt{3}\cdot sinC$， $\Delta ABC$的周长：$l=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot sinC$ $=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot sin(\cfrac{2\pi}{3}-B)$ $=3+2\sqrt{3}\cdot sinB+2\sqrt{3}\cdot (\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)$ $=3+3\sqrt{3}sinB+3cosB=3+6sin(B+\cfrac{\pi}{6})$ 因为$B\in(0，\cfrac{2\pi}{3})$，所以当$B=\cfrac{\pi}{3}$ 时，$\Delta ABC$的周长取得最大值，最大值为9。

八、考查数学表达式的取值范围

• 此时常利用三角函数求最大值

例9(2016宝鸡市第二次质量检测第17题) 在$\Delta ABC$中，已知$sin^2A+sin^2B+sinAsinB=sin^2C$，其中角$A、B、C$的对边分别为$a、b、c$， (1).求角$C$的大小。 (2).求$\cfrac{a+b}{c}$的取值范围。 分析：(1)角化边，由$\cfrac{a}{2R}=sinA，\cfrac{b}{2R}=sinB，\cfrac{c}{2R}=sinC$ 得到$a^2+b^2+ab=c^2$，即$a^2+b^2-c^2=-ab$， 故由余弦定理得到$cosC=\cfrac{a^2+b^2-c^2}{2ab}=-\cfrac{1}{2}$， 又$C\in (0，\pi)$，故$C=\cfrac{2\pi}{3}$。 (2)由(1)可知，$A+B=\cfrac{\pi}{3}$，即$A=\cfrac{\pi}{3}-B$ 边化角，由$a=2RsinA，b=2RsinB，c=2RsinC$ $\cfrac{a+b}{c}=\cfrac{sinA+sinB}{sinC}=\cfrac{2\sqrt{3}}{3}(sinA+sinB)$ $=\cfrac{2\sqrt{3}}{3}[sin(\cfrac{\pi}{3}-B)+sinB]=\cfrac{2\sqrt{3}}{3}[\cfrac{\sqrt{3}}{2}cosB-\cfrac{1}{2}sinB+sinB]$ $=\cfrac{2\sqrt{3}}{3}(\cfrac{1}{2}sinB+\cfrac{\sqrt{3}}{2}cosB)=\cfrac{2\sqrt{3}}{3}sin(B+\cfrac{\pi}{3})$， 又由$ $$\begin{cases}B >0\\ \cfrac{\pi}{3}-B >0\end{cases}$$ $得到$0< B 故$\cfrac{\pi}{3}< B+\cfrac{\pi}{3} 则$\cfrac{\sqrt{3}}{2} < sin(B+\cfrac{\pi}{3})\leq 1$ 则有$1 即$\cfrac{a+b}{c}$的取值范围为$(1，\cfrac{2\sqrt{3}}{3}]$。 引申：上述思路可以求解$msinB+nsinC$的取值范围($m、n$是实数)。 引申例9 在锐角三角形$ABC$中，$C=2B$,则$\cfrac{c}{b}$的取值范围是$(\sqrt{2}，\sqrt{3}）$ 分析：本题先将$\cfrac{c}{b}=\cfrac{sinC}{sinB}=2cosB$， 接下来的难点是求$B$的范围，注意列不等式的角度，锐角三角形的三个角都是锐角，要同时限制 由$\begin{cases}&0< A $\begin{cases} &0 < \pi-3B 解得$B \in (\cfrac{\pi}{6}，\cfrac{\pi}{4})$，故$\cfrac{c}{b}=2cosB \in (\sqrt{2}，\sqrt{3}）$。 例10在锐角$\Delta ABC$中，内角$A、B、C$的对边分别是$a、b、c$，且满足$(a-b)(sinA+sinB)=(c-b)sinC$， 若$a=\sqrt{3}$，则$b^2+c^2$的取值范围是【】 $A.(3，6]$. $\hspace{4em}$ $B.(3，5)$. $\hspace{4em}$ $C.(5，6]$. $\hspace{4em}$ $D.[5，6]$. 分析：由已知和正弦定理可知， $(a-b)(a+b)=(c-b)c$，即$bc=b^2+c^2-a^2$， 故$cosA=\cfrac{1}{2}$，由$A\in (0，\pi)$，可知$A=\cfrac{\pi}{3}$。 则$B+C=\cfrac{2\pi}{3}$，又由于是锐角$\Delta ABC$， 则$\left\{\begin{array}{l}{0< B < \cfrac{\pi}{2}}\\{0 则得到$\cfrac{\pi}{6}< B < \cfrac{\pi}{2}$； 又$a=\sqrt{3}$，则$2R=\cfrac{a}{sinA}=2$， 所以$b^2+c^2=(2RsinB)^2+(2RsinC)^2$ $=(2R)^2(sin^2B+sin^2C)$ $=4(sin^2B+sin^2(\cfrac{2\pi}{3}-B))$ $=4[sin^2B+(\cfrac{\sqrt{3}}{2}cosB+\cfrac{1}{2}sinB)^2]$ $=4(sin^2B+\cfrac{3}{4}cos^2B+\cfrac{1}{4}sin^2B+2\cdot \cfrac{\sqrt{3}}{2}cosB\cdot \cfrac{1}{2}sinB)$ $=4(\cfrac{3}{4}+\cfrac{1}{2}sin^2B+\cfrac{\sqrt{3}}{4}sin2B)$ $=4[\cfrac{1}{4}(1-cos2B)+\cfrac{\sqrt{3}}{4}sin2B+\cfrac{3}{4}]$ $=\sqrt{3}sin2B-cos2B+4$ $=2sin(2B-\cfrac{\pi}{6})+4$， 由上可知，$\cfrac{\pi}{6}< B < \cfrac{\pi}{2}$， 则$\cfrac{\pi}{3}< 2B $\cfrac{\pi}{6}< 2B-\cfrac{\pi}{6} < \cfrac{5\pi}{6}$ 则$\cfrac{1}{2}< sin(2B-\cfrac{\pi}{6})\leq 1$ 则$5<2sin(2B-\cfrac{\pi}{6})+4\leq 6$，故选C。

九、考查三角函数和向量的融合

• 此时常考查向量的坐标运算和三角变换，转化为正弦型后再考察其性质

例11【三角函数和解三角形和向量结合】 已知函数$f(x)=cosxsinx-\sqrt{3}cos^2x+\cfrac{\sqrt{3}}{2}$， (1)求函数$f(x)$的单调递增区间 分析：函数化简为$f(x)=sin(2x-\cfrac{\pi}{3})$，过程略，$[k\pi-\cfrac{\pi}{12}，k\pi+\cfrac{5\pi}{12}](k\in Z)$ (2)在$\Delta ABC$中，$A$为锐角且$f(A)=\cfrac{\sqrt{3}}{2}$，$\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD}$，$AB=\sqrt{3}$，$AD=2$，求$sin\angle BAD$。 分析：由$f(A)=sin(2A-\cfrac{\pi}{3})=\cfrac{\sqrt{3}}{2}$， 解得$A=\cfrac{\pi}{3}$或$A=\cfrac{\pi}{2}$(舍去)。 又由于$\overrightarrow{AB}+\overrightarrow{AC}=3\overrightarrow{AD}$， 如上图所示，$\overrightarrow{AB}+\overrightarrow{AC}=\overrightarrow{AE}=2\overrightarrow{AF}=2\cdot \cfrac{3}{2}\overrightarrow{AD}=3\overrightarrow{AD}$， 故点$D$为$\triangle ABC$的重心，以$AB$、$AC$为邻边做平行四边形$ABEC$， 由于$AD=2$，则$AE=6$， 在$\Delta ABE$中，$AB=3$，$\angle ABE=120^{\circ}$， 由正弦定理可得，$\cfrac{\sqrt{3}}{sin\angle AEB}=\cfrac{6}{\cfrac{\sqrt{3}}{2}}$， 可得$sin\angle AEB=\cfrac{1}{4}$ ，$cos\angle AEB=\cfrac{\sqrt{15}}{4}$， 故$sin\angle BAD=sin(\cfrac{\pi}{3}-\angle AEB)$ $=\cfrac{\sqrt{3}}{2}\times \cfrac{\sqrt{15}}{4}-\cfrac{1}{2}\times \cfrac{1}{4}=\cfrac{3\sqrt{5}-1}{8}$。 解后反思：利用已知的向量三角形，巧妙的构造了一个三角形，这样就能利用正弦定理和两角差的正弦公式求解了。

十、考查四边形的某条边的取值范围，动态变化

• 将四边形动态变化为三角形，从而求解四边形的某条边的取值范围

例12【2015$\cdot$全国卷Ⅰ】

在平面四边形$ABCD$中，$\angle A=\angle B=\angle C=75^{\circ}$，$BC=2$，则$AB$的取值范围是___________。

分析：本题目非常特别，依据题意我们做出的图形是平面四边形，

当我们将边$AD$平行移动时，题目的已知条件都没有改变，故想到将此静态图变化为动态图，

平行移动$AD$时，我们看到了两个临界位置，即四边形变化为三角形的两个状态，

其一是四边形变化为三角形$ABF$，此时应该有$BF<AB$；

其二是四边形变化为三角形$ABE$，此时应该有$BE>AB$；

故动态的边$AB$的范围是$BF<AB<BE$，从而求解。

解答：如图所示，延长$BA$与$CD$交于$E$，过$C$做$CF//AD$交$AB$于$F$，则$BF<AB<BE$；

在等腰三角形$CFB$中，$\angle FCB=30^{\circ}$，$CF=BC=2$，由余弦定理得到$BF=\sqrt{6}-\sqrt{2}$；

在等腰三角形$ECB$中，$\angle CEB=30^{\circ}$，$\angle ECB=75^{\circ}$，$BE=CE，BC=2$，

由正弦定理得到$BE=\sqrt{6}+\sqrt{2}$；

故$\sqrt{6}-\sqrt{2}<AB<\sqrt{6}+\sqrt{2}$

解后反思引申：

1、求$CD$的取值范围；

分析：由上述的动态图可知，$0<CD<CE=BE=\sqrt{6}+\sqrt{2}$；

2、求$AD$的取值范围；

分析：由上述的动态图可知，$0<AD<CF=BC=2$；

3、求四边形$ABCD$的周长的取值范围；

分析：四边形$ABCD$的周长介于$\Delta BCF$的周长和$\Delta BCE$的周长之间，

故其取值范围是$(4+\sqrt{6}-\sqrt{2}，2(\sqrt{6}+\sqrt{2})+2)$；

4、求四边形$ABCD$的面积的取值范围；

分析：四边形$ABCD$的面积介于$\Delta BCF$的面积和$\Delta BCE$的面积之间，

$S_{\Delta BCF}=\cfrac{1}{2}\times 2\times 2\times sin30^{\circ}=1$；

$S_{\Delta BCE}=\cfrac{1}{2}\times (\sqrt{6}+\sqrt{2})\times (\sqrt{6}+\sqrt{2})\times sin30^{\circ}=2+\sqrt{3}$；

故其取值范围是$(1，2+\sqrt{3})$；

十一、考查三角函数和恒成立命题的结合

• 先将恒成立问题转化为最值，这样原问题就转化为三角函数的问题了

例13(宝鸡市二检文科理科第17题) 已知函数$f(x)=4sinxsin(x+\cfrac{\pi}{3})$，在$\Delta ABC$中，角$A、B、C$的对边分别是$a、b、c$， (1)、当$x\in [0，\cfrac{\pi}{2}]$时，求函数$f(x)$的取值范围。 分析：先将函数变形为正弦型函数$f(x)=2sin(2x-\cfrac{\pi}{6})+1$，其中$x\in [0，\cfrac{\pi}{2}]$， 题目转化为正弦型函数在限定区间上的值域问题，常规题目，$f(x)\in [0，3]$ (2)、若对任意的$x\in R$，都有$f(x)\leq f(A)$，$b=2$，$c=4$，点$D$是边$BC$的中点，求$AD$的长。 【解答的共有部分】对任意的$x\in R$，都有$f(x)\leq f(A)$，则$f(A)=f(x)_{max}$； $f(x)=2sin(2x-\cfrac{\pi}{6})+1，x\in R$，则$f(x)_{max}=3$， 即$f(A)=3$又$f(A)=2sin(2A-\cfrac{\pi}{6})+1$ 故有$=2sin(2A-\cfrac{\pi}{6})+1=3$，即$sin(2A-\cfrac{\pi}{6})=1$， 即$2A-\cfrac{\pi}{6}=\cfrac{\pi}{2}$，故$A=\cfrac{\pi}{3}$。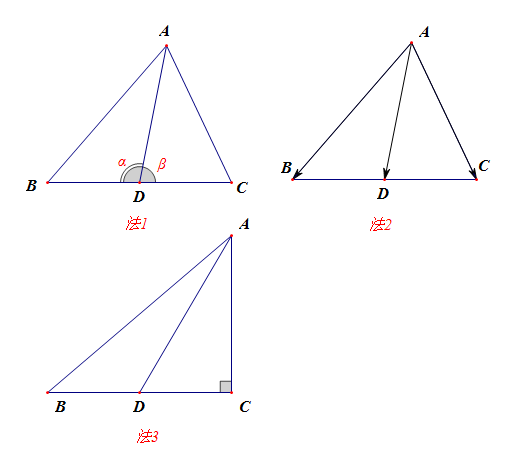 【法1】：余弦定理法，先由余弦定理得到$BC=2\sqrt{3}$，则$BD=CD=\sqrt{3}$， 设$\angle ADB=\alpha$，$\angle ADC=\beta$，则有$cos\alpha+cos\beta=0$。 再设$AD=x$，又$cos\alpha=\cfrac{x^2+(\sqrt{3})^2-4^2}{2\cdot\sqrt{3}\cdot x}$； $cos\beta=\cfrac{x^2+(\sqrt{3})^2-2^2}{2\cdot\sqrt{3}\cdot x}$； 代入方程$cos\alpha+cos\beta=0$得到，$x=AD=\sqrt{7}$。 【法2】：要求$AD$，由$AD=|\overrightarrow{AD}|$，而$|\overrightarrow{AD}|=\sqrt{\overrightarrow{AD}^2}$， $\overrightarrow{AD}=\cfrac{1}{2}(\overrightarrow{AB}+\overrightarrow{AC})$ 则$\overrightarrow{AD}^2=\cfrac{1}{4}(\overrightarrow{AB}+\overrightarrow{AC})^2$ 则$|\overrightarrow{AD}|^2=\cfrac{1}{4}(|\overrightarrow{AB}|^2+|\overrightarrow{AC}|^2+2|\overrightarrow{AB}||\overrightarrow{AC}|cos60^{\circ})$ $=\cfrac{1}{4}(4^2+2^2+2\times4\times2\times\cfrac{1}{2})=7$ 故$AD=|\overrightarrow{AD}|=\sqrt{7}$； 【法3】由题目可知，先由余弦定理得到$BC=2\sqrt{3}$，则由$AB=4，AC=2$， 可知$\Delta ABC$为$Rt\Delta$， 则有$AC=2$，$CD=\sqrt{3}$，故由勾股定理可知，$AD=\sqrt{7}$。 解后反思： 1、向量法和余弦定理法都是大家应该掌握的常见的思路方法， 其中向量法这个思路，对学生和老师而言，都不是那样的自如应用。

十二、考查解三角形的实际应用

• 此时常先建立解三角形的数学模型，然后利用正余弦定理求解，需要注意立体问题平面化，不同三角形中的要素统一化到同一个三角形中。

例14 解三角形的实际应用