线代——求逆矩阵的快捷方法_分块矩阵abcd求逆口诀

通常，求逆矩阵有两种方法：
方法一：

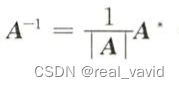
方法二：

但是，对于特殊矩阵，如:

1、二阶矩阵

A = [ a b c d ] A =

$$\begin{bmatrix} a & b\\ c & d \end{bmatrix}$$ A=[ac​bd​]，其逆矩阵 $A^{-1}=\frac{1}{ad-bc}\left[\begin{array}{cc}d& -b\\ -c& a\end{array}\right]$

2、分块矩阵

---

分块矩阵在主对角位置，直接对分块矩阵取逆矩阵：

A = [ X Y ] A =

$$\begin{bmatrix} X & \\ & Y \end{bmatrix}$$ A=[X​Y​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}{X}^{-1}& \\ & Y^{-1}\end{array}\right]$

---

分块矩阵在副对角位置，副对调，再取逆：

A = [ X Y ] A =

$$\begin{bmatrix} & X \\ Y & \end{bmatrix}$$ A=[Y​X​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}& Y^{-1}\\ X^{-1}& \end{array}\right]$

---

分块矩阵为右上三角形状，首先主对角直接取逆，然后再对右上角子矩阵左乘其行，右乘其列，再添符号：

A = [ X W Y ] A =

$$\begin{bmatrix} X & W\\ & Y \end{bmatrix}$$ A=[X​WY​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}{X}^{-1}& -X^{-1}W{Y}^{-1}\\ & Y^{-1}\end{array}\right]$

同理，对于左下三角形状，首先主对角直接取逆，然后再对左下角子矩阵左乘其行，右乘其列，再添符号：

A = [ X W Y ] A =

$$\begin{bmatrix} X & \\ W & Y \end{bmatrix}$$ A=[XW​Y​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}{X}^{-1}& \\ -Y^{-1}W{X}^{-1}& Y^{-1}\end{array}\right]$

它们相同之处，都是分块三角矩阵占据主对角位置。

---

分块矩阵为左上三角形状，首先副对调，再取逆，然后将左上角子矩阵换到右下角，最后再对该子矩阵左乘其行，右乘其列，再添符号：

A = [ W X Y ] A =

$$\begin{bmatrix} W & X \\ Y & \end{bmatrix}$$ A=[WY​X​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}& Y^{-1}\\ X^{-1}& -X^{-1}W{Y}^{-1}\end{array}\right]$

同理，对于右下三角形状，首先副对调，再取逆，然后将右下角子矩阵换到左上角，最后再对该子矩阵左乘其行，右乘其列，再添符号：

A = [ X Y W ] A =

$$\begin{bmatrix} & X \\ Y & W \end{bmatrix}$$ A=[Y​XW​]，其逆矩阵 $A^{-1}=\left[\begin{array}{cc}-Y^{-1}W{X}^{-1}& Y^{-1}\\ X^{-1}& \end{array}\right]$

它们相同之处，都是分块三角矩阵占据副对角位置。

---

综上，对于形状是上、下三角的分块矩阵求逆，如果分块子矩阵占据主对角位置，不需要对调位置；如果分块子矩阵占据副对角位置，都需要对调位置。