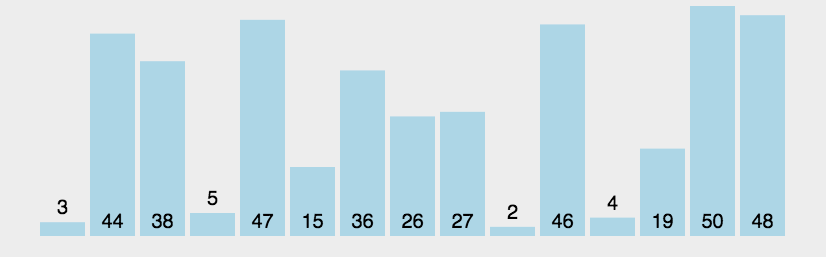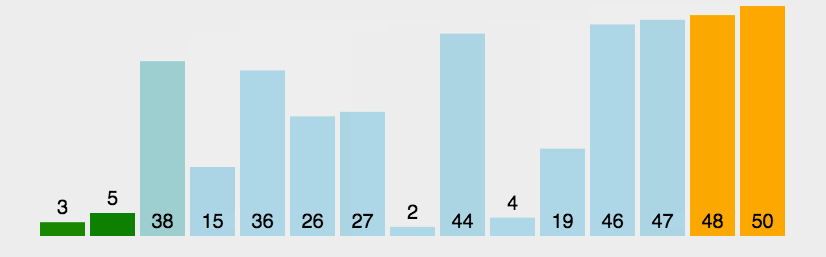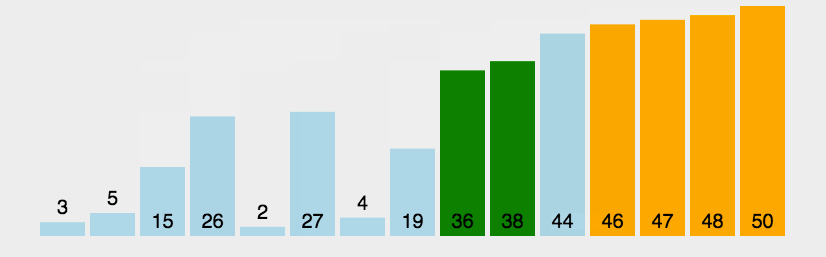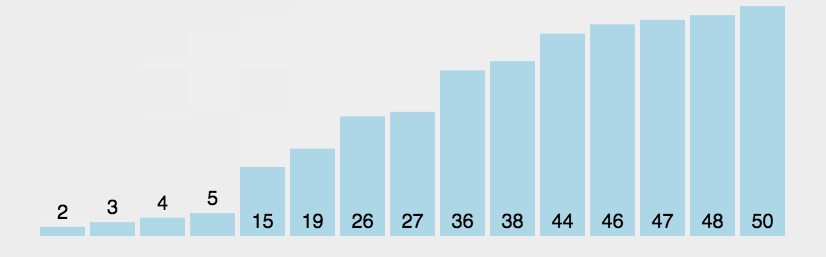冒泡排序是一种很好理解的排序，冒泡排序的整体原则就是将数组进行遍历，从下标为0的地方开始，让相邻的两个元素之间进行比较，如果你要从小到大进行排序，就让相邻的两个元素中较大的值放在较小的值的后面，从待排元素的位置开始，一直遍历到未排序的末尾，每次都比较两个元素，把大的元素放在后面，等到遍历完成数组，放在最后的那个元素就是最大的。

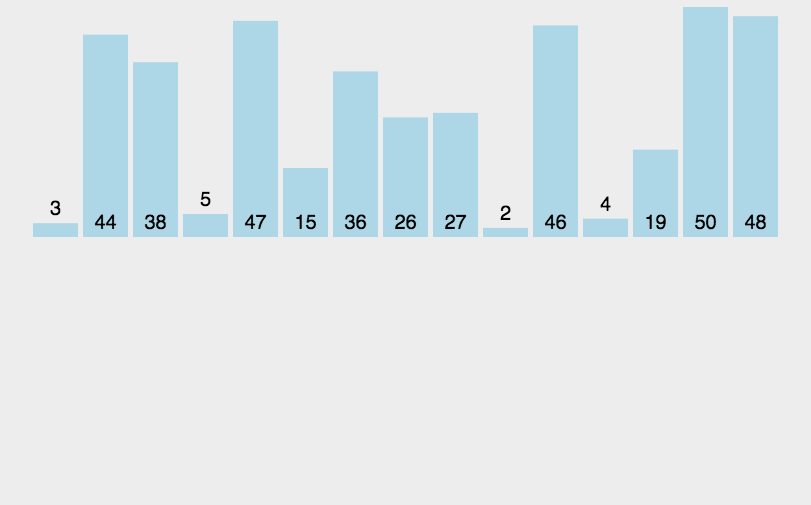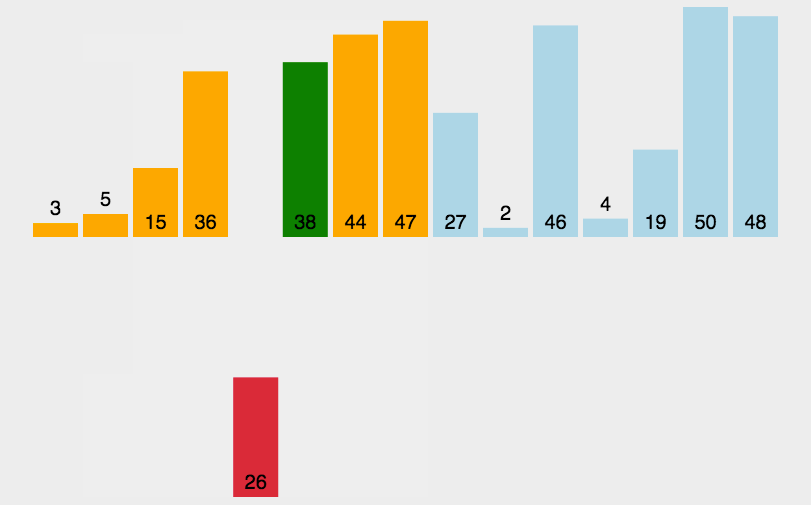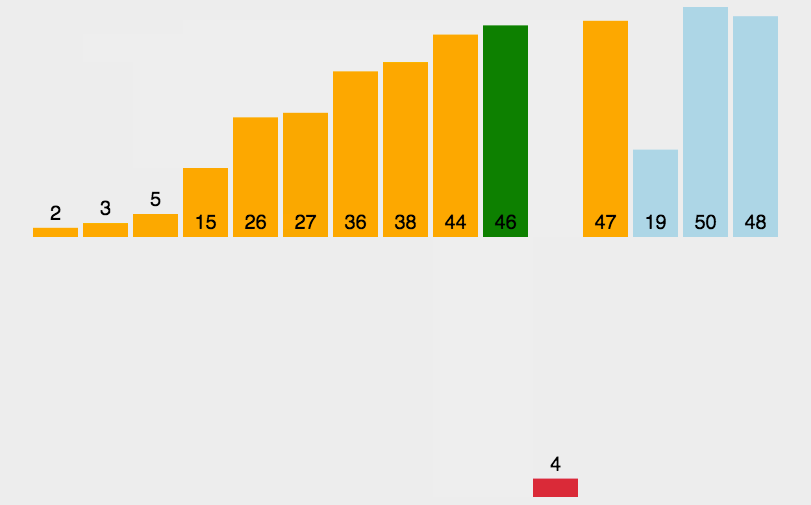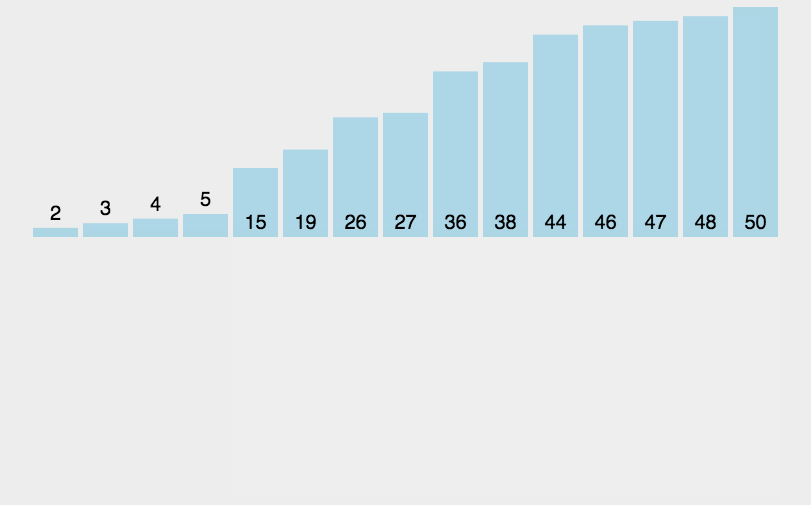
参见下图：

我们根据思路进行冒泡排序的时间复杂度的分析：

因为确定一个元素的位置的时候我们需要进行一次数组的遍历，而整个数组的每个元素我们都需要为他单独的进行一次数组的遍历，所以整个过程的时间复杂度就是O(N^2)，空间复杂度是O(1).

代码实现：
public class BubbleSort {
    public static void bubbleSort(int[] array){
        boolean flag = false;
        for(int i = 0; i < array.length -1; i++){
            for(int j = 0; j < array.length - 1 - i; j++){
                if(array[j] > array[j + 1]){
                    flag = true;
                    int temp = array[j];
                    array[j] = array[j + 1];
                    array[j + 1] = temp;
                }
            }
            if(!flag){
                break;
            }
        }
    }
}
因为不管数组是否有序，我们都要进行循环两次的遍历，那么我们的带牌数组如果本来就有序，会白白浪费很多时间，所以我们进行了优化，flag如果在第一次比较的过程中没有改变，说明这个数组已经有序，直接break就行。

选择排序：

选择排序的思路：

选择排序采用的方法也很巧妙，顾名思义，选择排序就是选择数字然后填数。

我们定义一个指针可以遍历整个数组，先从 0下标的位置开始，从0的后面选一个最小的数字（或者最大的数字），让这个最小的数字与0下标的数字交换位置，完成0下标上位置的确定。然后指针定位到1下标，重复上述的过程就能把整个数组排完序。

选择排序的复杂度分析：

选择排序每一个元素都要和整个数组剩下未排序的元素比较一次，因此时间复杂度就是O(N^2),空间复杂度是O(1);

代码实现：


public class SlectSort {
    public static void slectSort(int[] array){
        slect(array);
    }
    private static void slect(int[] array){
 
        for(int i = 0; i < array.length; i++){
            int minindex = i;
            for(int j = i + 1; j <array.length; j++){
                if(array[minindex] > array[j]){
                    minindex = j;
                }
            }
            if(i != minindex){
                swap(array,i,minindex);
            }
        }
    }
    private static void swap(int[] array,int i,int minindex){
        int temp = array[i];
        array[i] = array[minindex];
        array[minindex] = temp;
    }
}

插入排序：

想必大家都玩过扑克牌，我们抓拍后插牌的操作就是插入排序，具体的操作是怎么实现的？想一想玩牌的时候是不是找到了一个前面比待插入牌小的数，后面比待插入牌大的数，然后在这中间进行插入？

按照这样的思路，我们首先把数组中的第一个元素看成有序的，从第二个元素开始，往前找，如果前面的元素小于待排序的数，那么让前面的元素移动到后面，直到前面的元素小于

待排序的元素，然后把待排序的元素插入到两个元素之间就行。

插入排序的复杂度分析：

针对数组的每一个元素，都需要与前面已排序的元素进行比较，最坏的情况下每次每个元素都要进行比较，时间复杂度就是O(n^2),值得注意的是，插入排序对于趋近于有序的数据排序的速度要大于趋近于无序的数据的排序速度，换句话来说，数据越有序，使用插入排序排序的速度就越快。这一特点会在后续的希尔排序中使用到。

代码实现：
public class InsertSort {
    public static void insertSort(int[] array){
        for(int i = 1; i < array.length; i++){
            int j = i -1;
            int temp = array[i];
            for(; j >= 0; j--){
                if(array[j] > temp){
                    array[j + 1] = array[j];
                }else{
                    break;
                }
            }
            array[j + 1] = temp;
        }
    }
}

希尔排序：

希尔排序原理也是插入排序的原理，他和插入排序的结构很相似，但是对插入排序的最坏情况，也就是趋近于无序的情况进行了改进。

希尔排序的整体思路与插入排序相同，不过每次互相比较的两个元素的步长发生了改变，

确定的步长通常使用数组整体的长度 / 2 ，直到步长等于1的时候就可以停止。

通过划分步长，每次的互相间隔为步长的元素之间进行插入排序，随着步长的减少，数组会越来越趋近于有序，我们就能在步长gap == 1 的时候获得一个趋近于有序的数组，这样在对整体进行插入排序，会杜绝插入排序的时候最坏的情况发生。

希尔排序的复杂度分析：

平均情况下，希尔排序的时间复杂度是O(Nlogn)，在最坏的情况下希尔排序的时间复杂度是O(N^2),由于没有开辟新的空间，所以空间复杂度就是O(1);

值得一提的是，对于小数组，数据量不是很大的时候，希尔排序的速度有的时候会比快速排序和堆排序要快，但是涉及到大量的数据的时候，就没有快速排序和堆排序快了。

代码实现：


public class ShellSort {
    public static void shellSort(int[] array){
        int gap = array.length;
        while(gap > 1){//希尔排序的步长
            gap /= 2;
            shell(array,gap);
        }
    }
    public static void shell(){
    }
    private static void shell(int[] array, int gap){
       for(int i = gap; i < array.length; i++){
           int j = i - gap;
           int temp = array[i];
           for(;j >= 0; j -= gap){
               if(array[j] > temp){
                   array[j + gap] = array[j];
               }else{
                   break;
               }
           }
           array[j + gap] = temp;
       }
    }
}

堆排序：

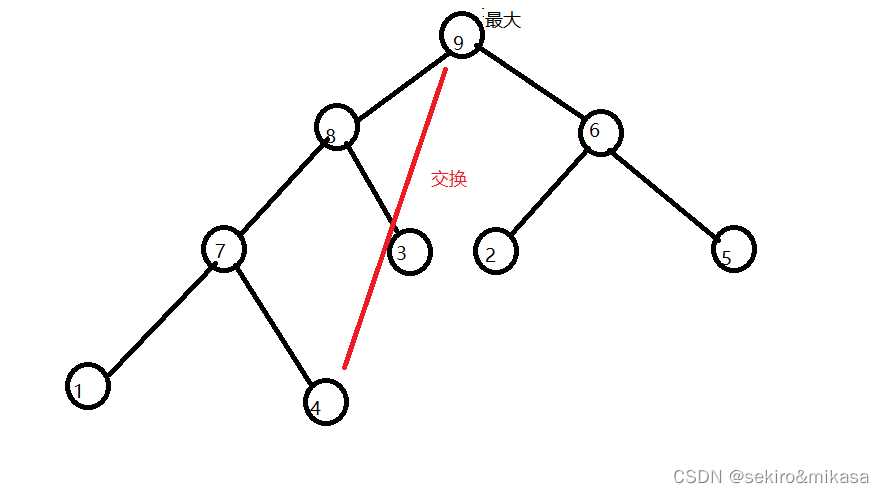
堆排序的思路非常简单，利用优先级队列就可以实现，以从大到小排列一个数组为例，首先建立一个大根堆，堆顶的元素一定是堆中最大的一个，我们只需要将栈顶的元素与栈尾的元素进行交换，然后让堆的长度减少一个，这样堆中的数组的最后一个元素就是整个数组中最大的值了，然后利用减少一个长度的堆继续维护最大值，直到长度减小到0为止。

如图，9 和 4 交换完成之后，长度减一，以减一以后的长度再维护一个大根堆，重复上述的操作，直到长度变为0；

堆排序的复杂度分析：

堆排序是一种选择排序，整体主要由构建初始堆+交换堆顶元素和末尾元素并重建堆两部分组成。其中构建初始堆经推导复杂度为O(n)，在交换并重建堆的过程中，需交换n-1次，而重建堆的过程中，根据完全二叉树的性质，[log2(n-1),log2(n-2)...1]逐步递减，近似为nlogn。所以堆排序时间复杂度一般认为就是O(nlogn)级。

代码实现：


import java.util.Arrays;
 
public class MyHeap {
    public int[] elem ;
    public int DEFAULTINT = 10;
    public int usizesize = 0;
 
    @Override
    public String toString() {
        return "MyHeap{" +
                "elem=" + Arrays.toString(elem) +
                '}';
    }
 
    public void SetHeap(){
        elem = new int[DEFAULTINT];
    }
    public void InitHeap(int[] array){
        for(int i = 0; i < array.length; i++){
            elem[i] = array[i];
            usizesize ++ ;
        }
    }
    public void creatHeap(){
        for(int parent = (usizesize - 1 - 1) / 2; parent >= 0; parent--){
            shift(parent,usizesize);
        }
    }
    public void offer(int val){
        if(isFull()){
            elem = Arrays.copyOf(this.elem, 2*elem.length);
        }
        elem[usizesize] = val;
        usizesize++;
        shilftUp(usizesize - 1);
 
    }
    public void pop(){
        if(isEmpty()){
            //异常
            return ;
        }
        int temp = elem[0];
        elem[0] = elem[usizesize - 1];
        elem[usizesize - 1] = temp;
        usizesize--;
        shilftDown(0,usizesize);
    }
    public void shilftDown(int parent,int len){
        int child = 2*parent + 1;
        while(child < len){
            if( child + 1  < len
                    && elem[child] < elem[child + 1]){
                child++;
            }
            if(elem[parent] < elem[child]){
                int temp = elem[child];
                elem[child] = elem[parent];
                elem[parent] = temp;
                parent = child;
                child = 2*parent + 1;
            }else{
                break;
            }
        }
    }
    public boolean isEmpty(){
        if(usizesize == 0){
            return true;
        }
        return false;
    }
    public void shilftUp(int child){
        int parent = (child - 1) / 2;
        while(child > 0){
            if(elem[parent]  < elem[child]){
                int temp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = temp;
                child = parent;
                parent = (child - 1) / 2;
            }else{
                break;
            }
        }
    }
    public boolean isFull(){
        if(usizesize == elem.length){
            return true;
        }else{
            return false;
        }
    }
    public void shift(int parent,int len){
        int child = 2*parent + 1;
        while(child < len){
            if(child + 1< len && elem[child] < elem[child + 1]) {
                child++;
            }
            if(elem[parent] < elem[child]){
                int temp = elem[parent];
                elem[parent] = elem[child];
                elem[child] = temp;
                parent =child;
                child = 2*parent + 1;
            }else{
                break;
            }
        }
    }
    public void heapSirt(){
        int end = usizesize - 1;
        while(end > 0){
            int temp = elem[0];
            elem[0] = elem[end];
            elem[end] = temp;
            shilftDown(0,end);
            end--;
        }
    }
}

快速排序：

快速排序作为一种在排序中运用非常普遍的排序，在整个排序的算法中占据着重要的地位，很多排序是作为快速排序的优化算法体现在快速排序中，所以快速排序的学习对我们至关重要。

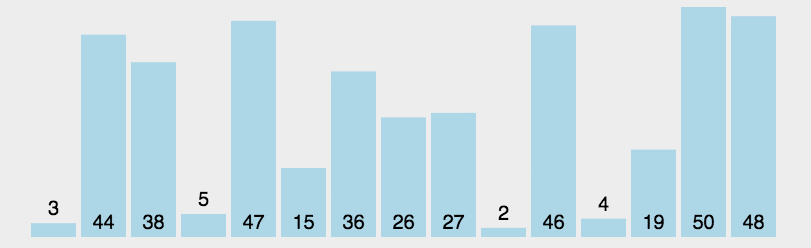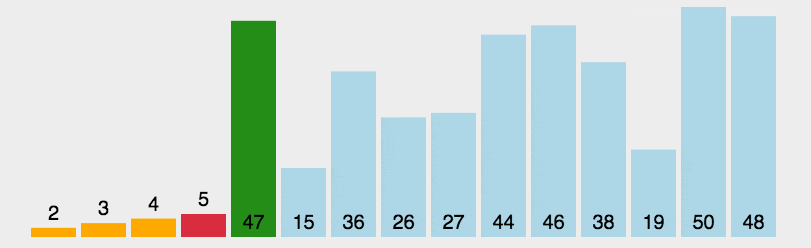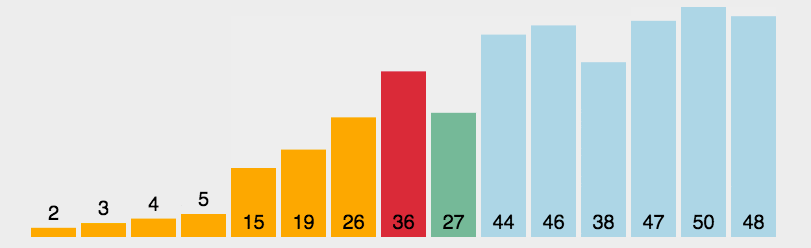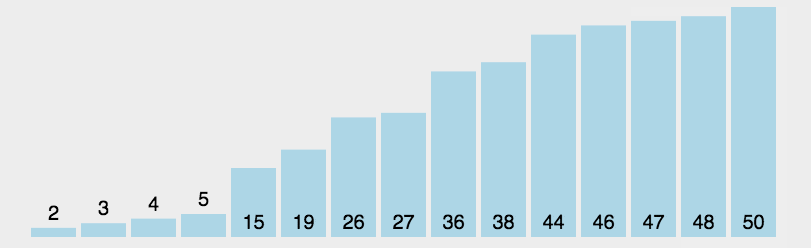
快速排序采用分治的方法进行排序，我们选择一个范围，在这个范围内，第一个数字当作key的值，在这个范围中，比key小的数字放在key的左边，比key大的数放在key的右边，这就完成了一个元素的排序，然后再对key左边和key右边进行这个操作。

快速排序对一个区间的排序有三种不同的方法：

1、hoare法

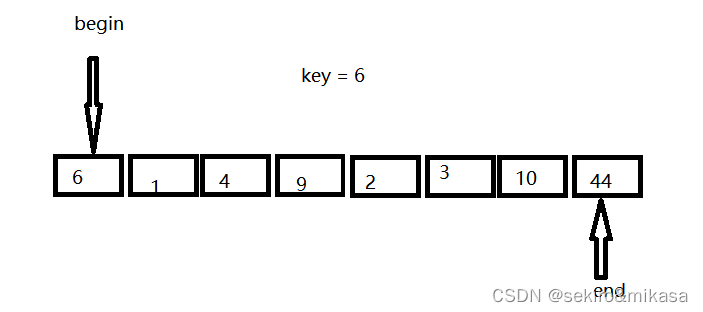
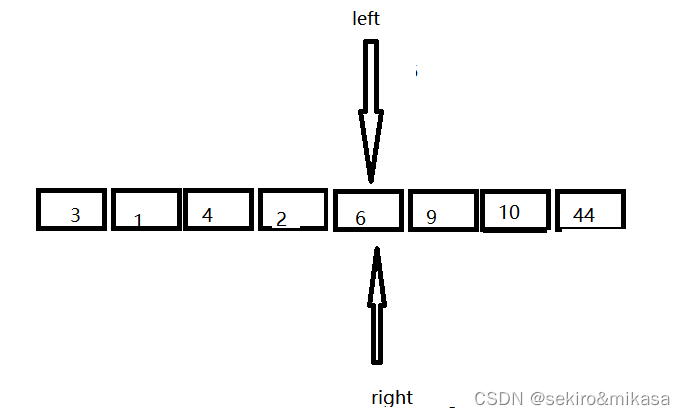
此方法在区间的前后定义两个指针，先从右边的指针进行查询，当遇到一个小key值的时候，就让左边和右边指针所对应的值进行交换，再从左边开始查询，当遇到一个比key大的值的时候就让左边和右边的值进行交换，重复上述操作，直到左边的指针与右边的指针相遇的时候结束，我们把key的值放进两个下边所对应的地方就完成了key的排序的确认，然后进行分治即可。

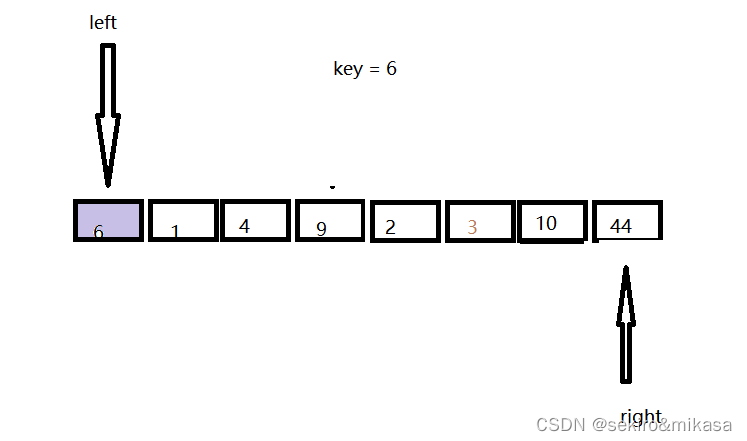
开始时定义两个指针：

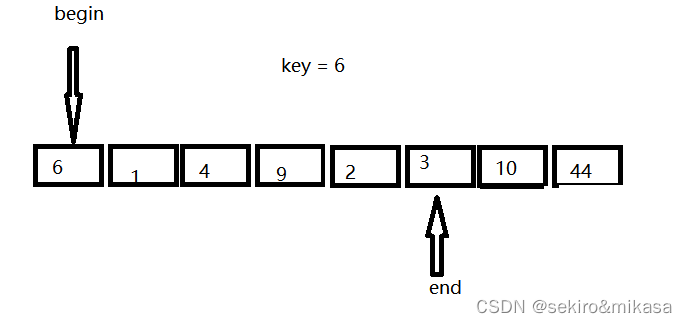
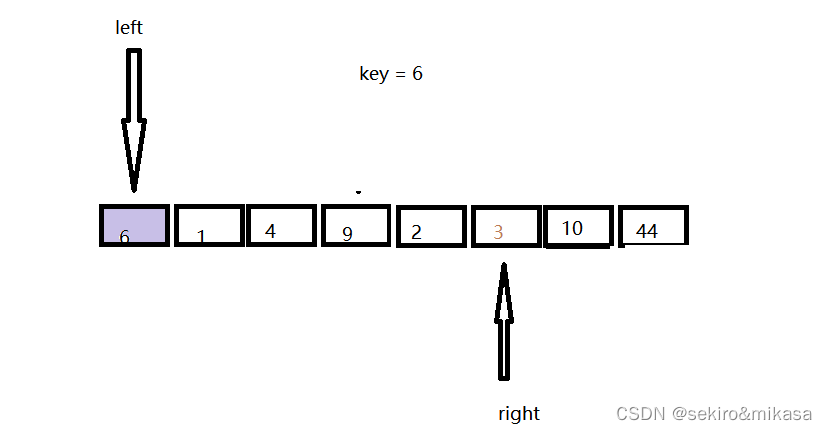
从右边开始找到第一个小于key的的值：

从左边找大于key的值：

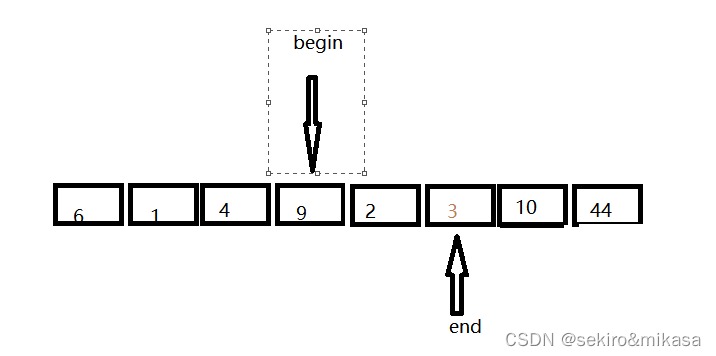
然后交换两个数：

继续移动指针，当指针相同的时候，交换key值和指针所指向的值：

到此第一次排序结束。

代码：
private static void swap(int[] array, int left, int right){
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;
    }
    public static int findindex2(int[] array, int left, int right){
        int i = left;
        int j = right;
        int key = array[left];
        while(i < j){
            while(i < j && array[j] >= key){
                j--;
            }
            while(i < j && array[i] <= key){
                i++;
            }
            swap(array,i,j);
        }
        swap(array,left,i);
        return i;
    }

2、挖坑法：

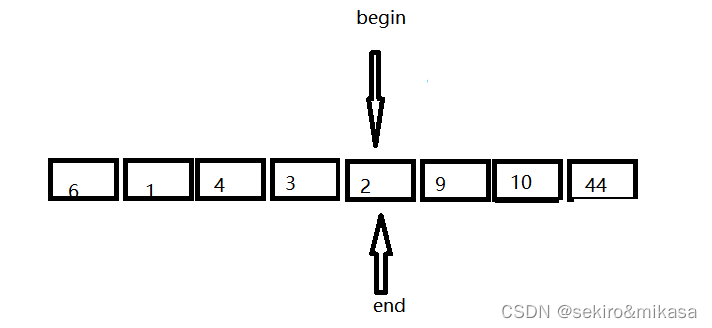
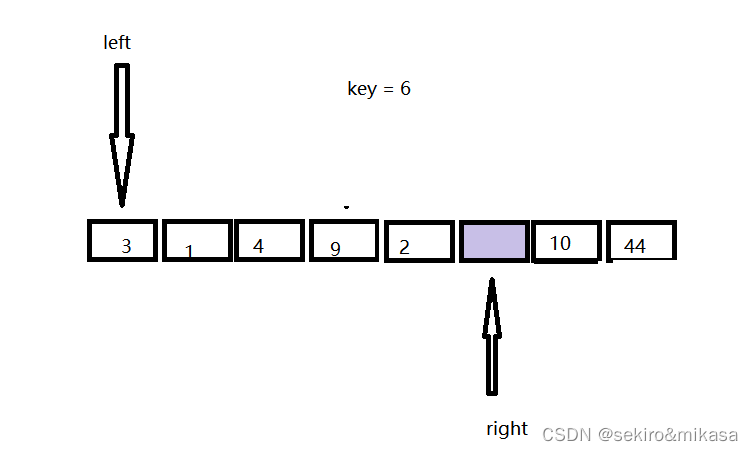
挖坑法是我们运用最普遍的一种方法，我们可以形象的把初始时key的值，也就是left下标的数值当作坑，先从右边开始进行遍历，当找到一个小于key的值的时候，将left下标的值替换成right下标的值，此时right下标的值就会变成坑，然后用left进行遍历，找到一个大于key的值，将此数填入right下面的值，重复此过程，到最后right和left下标重合的时候，我们将key填入下面，我们就完成了第一次的排序。

初始时刻，坑在left下标的位置：

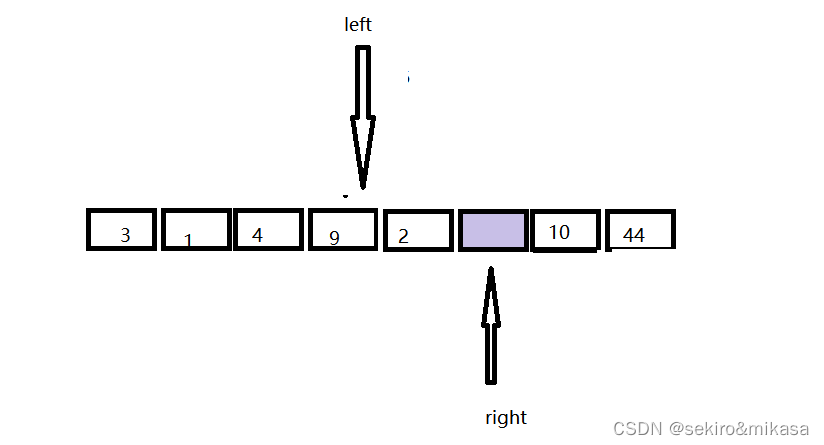
从右边开始找小于key的值：

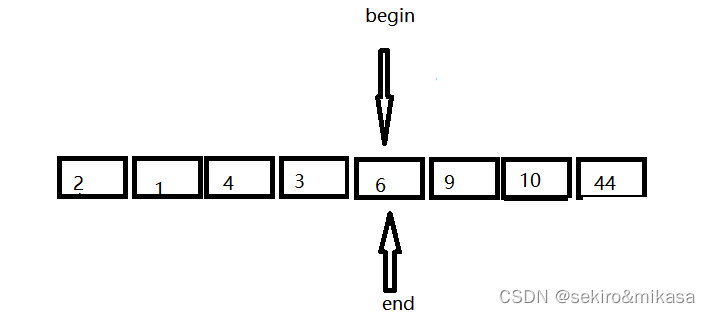
将这个值填入坑中，然后右边又变成了坑：

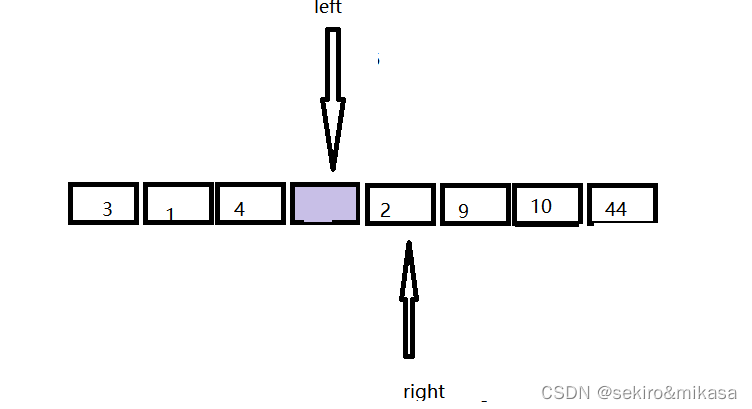
从左边找到一个大于key的值：

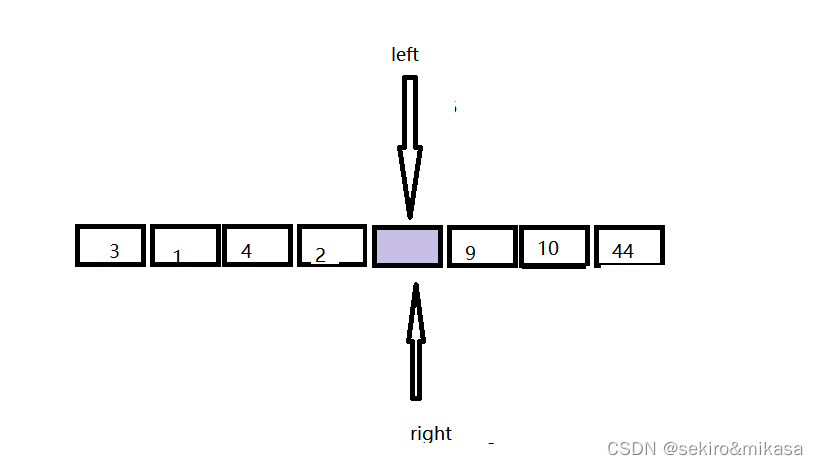
把次数字填入坑中，然后left变成坑：

最后一步将下标换成key，完成排序，之后进行递归：

代码：
 private static int findindex(int[] array, int left, int right){
        int key = array[left];
        while(left < right){
            while(left < right && array[right] >= key){
                right -- ;
            }
            array[left] = array[right];
            while(left < right && array[left] <= key){
                left ++;
            }
            array[right] = array[left];
        }
        array[left] = key;
        return left;
    }

前后指针法：

我们定义一个prev和cur，cur是prev的下一个值，我们让cur的值与key的值进行比较，如果cur的值大于key的值，我们就让cur++，prev不动，如果cur小于key，那么我们就让pre++，然后再判断pre与cur是否相等，如果相等就让cur++，然后在进行上述操作，如果不相等，就交换cur与prev的值。

代码：
    private static int partition(int[] array, int left, int right) {//前后指针法
        int prev = left ;
        int cur = left+1;
        while (cur <= right) {
            if(array[cur] < array[left] && array[++prev] != array[cur]) {
                swap(array,cur,prev);
            }
            cur++;
        }
        swap(array,prev,left);
        return prev;
    }

快速排序的复杂度分析：

时间复杂度：O(N*logN)。

最坏情况下能达到O(N^2)。

空间复杂度：O(logN) 。

快速排序的优化方案：

三位取中：

快速排序需要调整n个数字，每个数字调整的时间复杂度是logn，所以平均来说是O(logN),但是对于，我们是最坏的情况，我们需要用三位取中。三位取中它的思想是：选取数组开头，中间和结尾的元素，通过比较，选择中间的值作为快排的基准。


public static int findMid(int[] array,int left,int right){
        int i = left;
        int key = array[left];
        while(left < right){
            while (left < right && array[right] >= key){
                right--;
            }
            array[left]  =array[right];
            while (left < right && array[left] <= key){
                left++;
            }
            array[right] = array[left];
            }
            array[left] = key;
            return left;
        }
}

趋于有序时使用插入排序：


if(array.length < 7){
            //插入排序
            InsertSort.insertSort(array);
        }

快速排序完整代码：


 
import java.util.Arrays;
import java.util.HashMap;
 
public class Quck {
    public static int findMid(int[] array,int left,int right){
        int i = left;
        int key = array[left];
        while(left < right){
            while (left < right && array[right] >= key){
                right--;
            }
            array[left]  =array[right];
            while (left < right && array[left] <= key){
                left++;
            }
            array[right] = array[left];
            }
            array[left] = key;
            return left;
        }
        public static int findthreemid(int[] array,int start,int end){
            int mid = (start + end) / 2;
            if(array[start] < array[end]){
                if(array[mid] < array[start]){
                return start;
            }else if(array[mid] > array[end]){
                return end;
            }else{
                return mid;
            }
        }else{
            if(array[mid] < array[end]){
                return end;
            }else if(array[start] < array[mid]){
                return start;
            }else {
                return mid;
            }
        }
    }
    private static void swap(int[] array,int left,int right){
        int temp = array[left];
        array[left] = array[right];
        array[right] = temp;
    }
    public static void quickSort(int[] array,int start,int end){
        if(start >= end){
            return;
        }
        if(array.length < 7){
            //插入排序
            InsertSort.insertSort(array);
        }
        int index = findthreemid(array,start,end);
        swap(array,start,index);
        int position = findMid(array,start,end);
        quickSort(array,start,position - 1);
        quickSort(array,position + 1, end);
    }
    public static void quick_Sort(int[] arr) {
        quickSort(arr,0,arr.length - 1);
    }
}
 
public class InsertSort {
    public static void insertSort(int[] array){
        for(int i = 1; i < array.length; i++){
            int j = i -1;
            int temp = array[i];
            for(; j >= 0; j--){
                if(array[j] > temp){
                    array[j + 1] = array[j];
                }else{
                    break;
                }
            }
            array[j + 1] = temp;
        }
    }
    public static void insert(int[] nums){
        for(int i = 1; i < nums.length; i++){
            int j = i - 1;
            int temp = nums[i];
            for(; j >= 0; j--){
                if(temp < nums[j]){
                    nums[j + 1] =  nums[j];
                }else{
                    break;
                }
            }
            nums[j + 1] = temp;
        }
    }
}

归并排序：

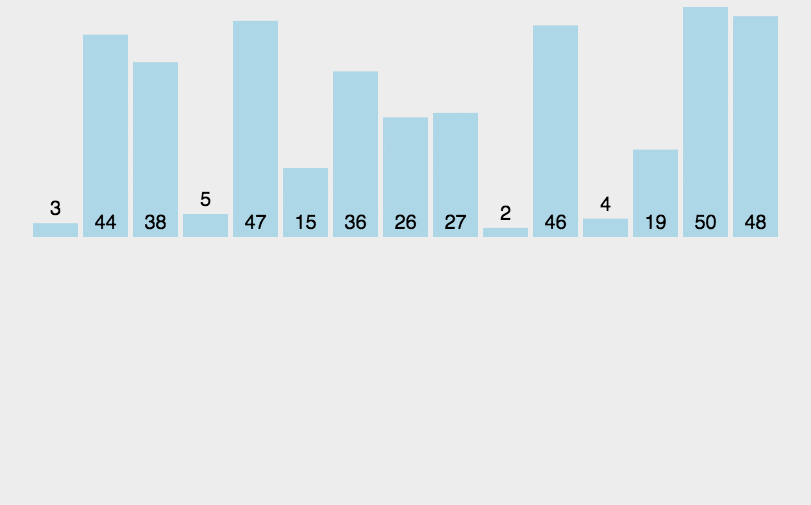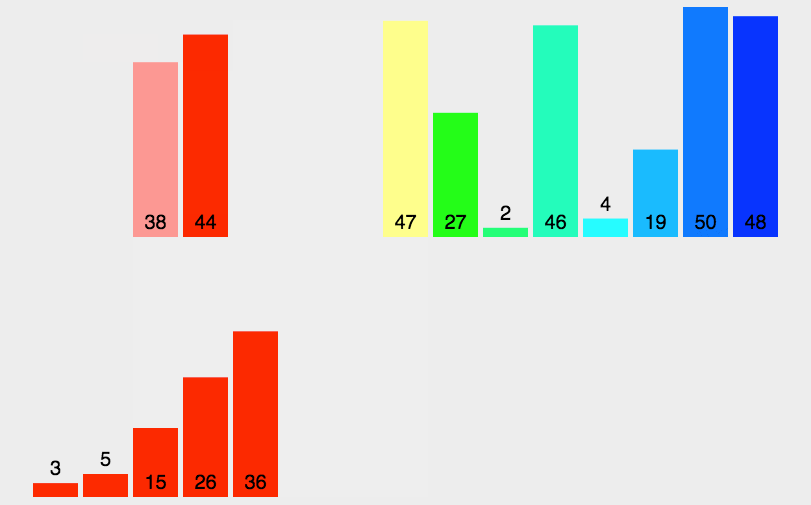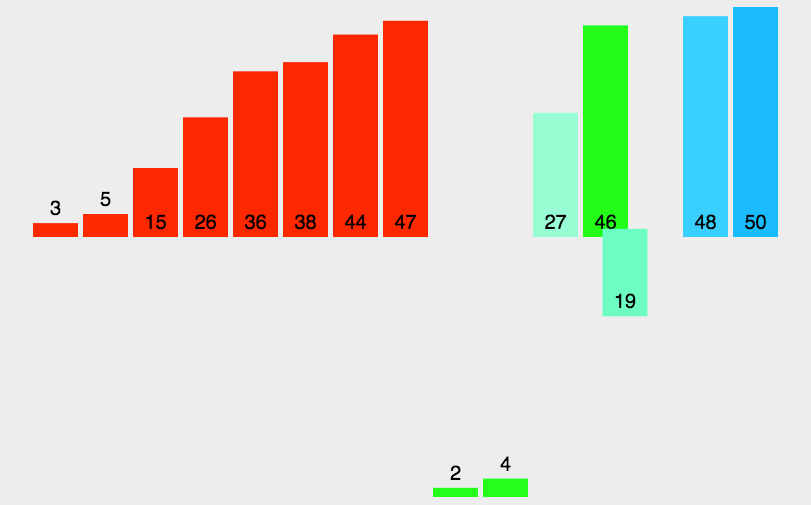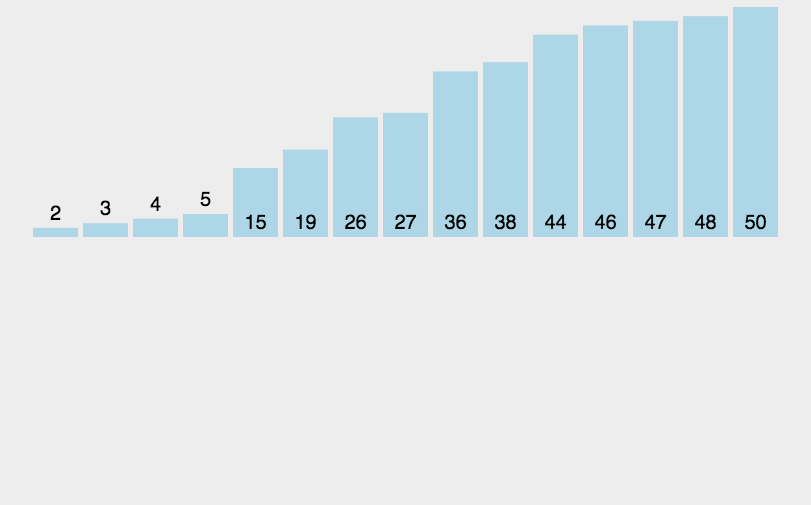
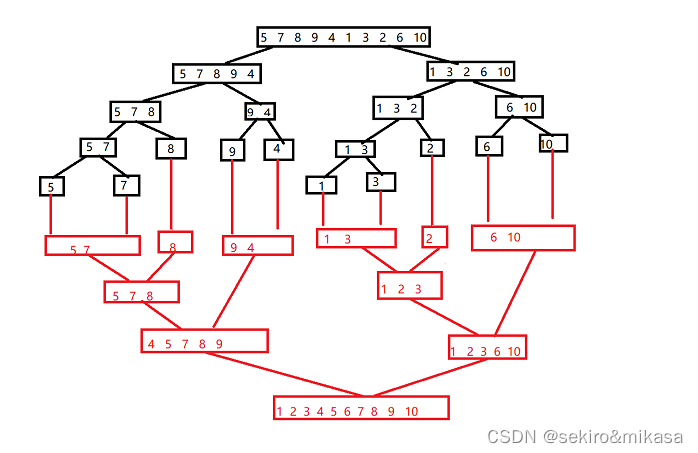
归并排序是把完整的数据每次取中，把分成的两个数据合并成一个有序的数据。

归并排序是建立在归并操作上的一种有效的排序算法,该算法是采用分治法的一个非常典型的应用。将已有序的子序列合并，得到完全有序的序列；即先使每个子序列有序，再使
子序列段间有序。若将两个有序表合并成一个有序表，称为二路归并。

归并排序复杂度分析：

时间复杂度：O(N* logN)

空间复杂度：由于每次合并都需要一个新的数组，所以就是O(N)

代码：


public class mergeSort {
    public static void mergeSort_(int[] array){
        merSort_Child(array,0,array.length - 1);
    }
    private static void merSort_Child(int[] array,int left,int right){
        if(left >= right){
            return;
        }
        int mid = (left + right) / 2;
        merSort_Child(array,left,mid);
        merSort_Child(array,mid + 1,right);
        merge(array,left,mid,right);
    }
    private static void merge(int[] array, int left, int mid, int right){
        int[] temp = new int[right - left + 1];
        int k = 0;
        int s1 = left;
        int e1 = mid;
        int s2 = mid  + 1;
        int e2 = right;
        while(s1 <= e1 && s2 <= e2){
            if(array[s1] <= array[s2]){
                temp[k++] = array[s1++];
            }else{
                temp[k++] = array[s2++];
            }
        }
        while (s1 <= e1){
            temp[k++] = array[s1++];
        }
        while(s2 <= e2){
            temp[k++] = array[s2++];
        }
        for(int i = 0; i < k; i++){
            array[i + left] = temp[i];
        }
    }
    public static void mergeSortfeidigui(int[] array) {
        int gap = 1;
        while (gap < array.length) {
            for (int i = 0; i < array.length; i += gap*2) {
                int left = i;
                int mid = left + gap -1;
                int right = mid+gap;
                if(mid >= array.length) {
                    mid = array.length-1;
                }
                if(right >= array.length) {
                    right = array.length-1;
                }
                merge(array,left,mid,right);
            }
            gap *= 2;
        }
    }

总结：

排序方法最好平均最坏空间复杂度稳定性
冒泡排序 O(n) O(n^2) O(n^2) O(1) 稳定
插入排序 O(n) O(n^2) O(n^2) O(1) 稳定
选择排序 O(n^2) O(n^2) O(n^2) O(1) 不稳定
希尔排序 O(n) O(n^1.3) O(n^2) O(1) 不稳定
堆排序 O(n * log(n)) O(n * log(n)) O(n * log(n)) O(1) 不稳定
快速排序 O(n * log(n)) O(n * log(n)) O(n^2) O(log(n)) ~ O(n) 不稳定
归并排序 O(n * log(n)) O(n * log(n)) O(n * log(n)) O(n) 稳定

声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】

七大排序算法，冒泡排序 选择排序 插入排序 希尔排序 堆排序 快速排序 归并排序的深度讲解_比较说明冒泡算法,选择算法,希尔排序算法

排序：

冒泡排序：

冒泡排序的思路：

我们根据思路进行冒泡排序的时间复杂度的分析：

代码实现：

选择排序：

选择排序的思路：

选择排序的复杂度分析：

代码实现：

插入排序：

插入排序的复杂度分析：

代码实现：

希尔排序：

希尔排序的复杂度分析：

代码实现：

堆排序：

堆排序的复杂度分析：

代码实现：

快速排序：

1、hoare法

代码：

2、挖坑法：

代码：

前后指针法：

代码：

快速排序的复杂度分析：

快速排序的优化方案：

三位取中：

趋于有序时使用插入排序：

快速排序完整代码：

归并排序：

归并排序复杂度分析：

代码：

总结：

七大排序算法，冒泡排序选择排序插入排序希尔排序堆排序快速排序归并排序的深度讲解_比较说明冒泡算法,选择算法,希尔排序算法