数据结构——二叉树的创建及其基本操作_1.建立二叉树,并对树进行操作 【功能要求】 (1)利用完全二叉树的性质建立一棵二

#include<iostream>
#include<time.h>
#include<Windows.h>
using namespace std;
#define SIZE 100
#pragma warning(disable:4996)
typedef struct node
{
	char data;
	struct node* lchild;
	struct node* rchild;

}*TNode,Tnode;
TNode createtree();//建立二叉树思路一
void Createtree(TNode &Tree/* 也可以传参为TNode *Tree或Tnode **Tree,不用这两种是引用可以减轻代码出错率 */);//建立二叉树思路二
/*二叉树整体建立思想就是利用递归进行元素存放*/
/*关于建立二叉树传参的一些解释说明
此处的TNode &Tree是直接对Tree指针进行引用，所以在给指针分配空间时不需要用(*Tree)->lchild;而是直接用Tree->lchild,当然这也体现
了方法一的简洁性，即直接放弃通过函数外传参函数内初始化参数而是直接将所有操作在函数内完成，并返回需要的数据。
*/
void Aprinttree(TNode T);//先序遍历输出二叉树
void Bprinttree(TNode T);//中序遍历输出二叉树
void Cprinttree(TNode T);//后序遍历输出二叉树
void floortree(TNode T);//层序遍历输出二叉树
void destroytree(TNode T);//销毁二叉树
int gettreeheight(TNode T);//获取二叉树的高度
void Sumnode(TNode T, int &sum);//获取二叉树的结点总数
int zeronodecount(TNode T, int &sum);//求叶子结点个数
int onenodecount(TNode T, int &sum);//求度为1的结点个数
int main()
{
	int sumnode=0;
	int zeronode = 0;
	int onenode = 0;
	int high;
	TNode T;
	cout << "请以先序遍历录入二叉树：";
	Createtree(T);//T = createtree()或Createtree(&T);
	cout << "先序遍历打印此二叉树结果为：";
	Aprinttree(T); cout << endl;
	cout << "中序遍历打印此二叉树结果为：";
	Bprinttree(T); cout << endl;
	cout << "后序遍历打印此二叉树结果为：";
	Cprinttree(T); cout << endl;
	cout << "层序遍历打印此二叉树结果为：";
	floortree(T); cout << endl;
	high = gettreeheight(T);
	cout << "此二叉树的高度为：" << high << endl;
	Sumnode(T, sumnode);
	cout << "此二叉树的结点个数为：" << sumnode << endl;
	zeronodecount(T, zeronode);
	cout << "此二叉树的叶子结点个数为：" << zeronode << endl;
	onenodecount(T, onenode);
	cout << "此二叉树的度为1的结点个数为：" << onenode << endl;
	cout << "此二叉树的度为2的结点个数为：" << zeronode-1 << endl;
	destroytree(T);
	return 0;
}
TNode createtree()//建立二叉树方法一
{
	Tnode *Tree;
	char ch;
	cin >> ch;
	if (ch == '#')Tree = NULL;
	else
	{
		Tree = new Tnode;
		Tree->data = ch;
		Tree->lchild = createtree();
		Tree->rchild = createtree();
	}
	return Tree;
}
void Createtree(TNode &Tree/* 也可以传参为TNode *Tree或Tnode **Tree,不用这两种是引用可以减轻代码出错率*/)//建立二叉树方法二
{
	char ch;
	cin >> ch;
	if (ch == '#')Tree = NULL;
	else
	{
		Tree = new Tnode;
		Tree->data = ch;
		Createtree(Tree->lchild);
	    Createtree(Tree->rchild);
	}
	/*这是传入参数为TNode *Tree或Tnode **Tree时对应的代码
	char ch;
	cin >> ch;
	if (ch == '#')*Tree = NULL;
	else
	{
		*Tree = new Tnode;
		(*Tree)->data = ch;
		Createtree(&(*Tree)->lchild);
		Createtree(&(*Tree)->rchild);
	}
	*/
}
void Aprinttree(TNode T)//先序遍历输出二叉树
{
	if(T)
	{
		cout << T->data;
		Aprinttree(T->lchild);
		Aprinttree(T->rchild);
	}
}
void Bprinttree(TNode T)//中序遍历输出二叉树
{
	if (T)
	{
		Bprinttree(T->lchild);
		cout << T->data;
		Bprinttree(T->rchild);
	}
}
void Cprinttree(TNode T)//后序遍历输出二叉树
{
	if (T)
	{
		Cprinttree(T->lchild);
		Cprinttree(T->rchild);
		cout << T->data;
	}
}
void floortree(TNode T)//层序遍历输出二叉树
{
	TNode temp[100];
	int in = 0, out = 0;
	temp[in++] = T;
	while (in > out)
	{
		if (temp[out])
		{
			cout << temp[out]->data;
			temp[in++] = temp[out]->lchild;
			temp[in++] = temp[out]->rchild;
		}
		out++;	
	}


}
void destroytree(TNode T)//销毁二叉树
{
	if (T != NULL)
	{
		destroytree(T->lchild);
		destroytree(T->rchild);
		delete T;
	}
}
int gettreeheight(TNode T)//获取二叉树的高度
{
	if (T == NULL)return 0;
	else
	{
		int m = gettreeheight(T->lchild);
		int n = gettreeheight(T->rchild);
		return m >= n ? m + 1 : n + 1;
	}
}
void Sumnode(TNode T,int &sum)//获取二叉树的结点总数
{
	if (T == NULL)return ;
	else 
	{
		Sumnode(T->lchild,sum);
		Sumnode(T->rchild, sum);
		sum ++;
	}
}
int zeronodecount(TNode T,int &sum)//求叶子结点个数
{
	if (T == NULL)return 0;
	int m = zeronodecount(T->lchild,sum);
	int n = zeronodecount(T->rchild,sum);
	if (m == 0 && n == 0)
	{
		sum++;
		return 1;
	}
	else return 1;
}
int onenodecount(TNode T, int &sum)//求度为1的结点个数
{
	if (T == NULL)return 0;
	int m = onenodecount(T->lchild, sum);
	int n = onenodecount(T->rchild, sum);
    if (m != n)
	{
		sum++;
		return 1;
	}
	else return 1;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
125
126
127
128
129
130
131
132
133
134
135
136
137
138
139
140
141
142
143
144
145
146
147
148
149
150
151
152
153
154
155
156
157
158
159
160
161
162
163
164
165
166
167
168
169
170
171
172
173
174
175
176
177
178
179
180
181
182
183
184
185
186
187
188
189
190
191
192
193
194
195
196

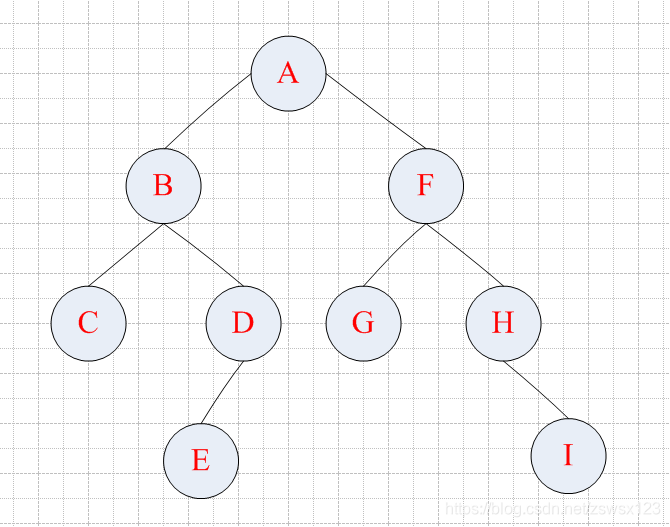
这是演示示例的逻辑结构图，本例中以编译器输入#为结束符号，即表示指向空
所以在编译器中的输入应为： ABC##DE###FG##H#I##
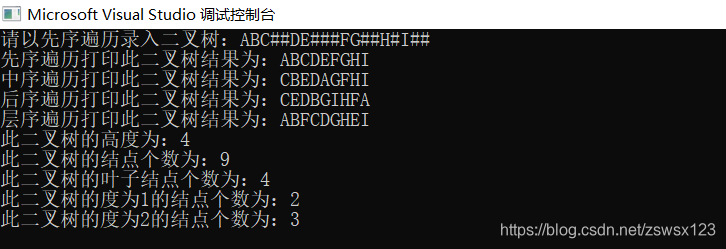
下图是对应代码的运行结果