激活函数 sigmoid、tanh、ReLu、Leaky ReLu、ELU、Maxout_excel sigmoid

1. sigmoid

sigmoid 是逻辑函数，常见的 sigmoid 函数定义为:
$$S(x)=\frac{1}{1+e^{-x}}$$

$$\frac{dS(x)}{dx}=\frac{e^{-x}}{{\left(1+e^{-x}\right)}^2}=\left(\frac{1+e^{-x}-1}{1+e^{-x}}\right)\left(\frac{1}{1+e^{-x}}\right)=(1-S(x))S(x)$$

广义逻辑函数：
$$f(x)={\left(1+e^{-x}\right)}^{-\alpha },\alpha >0$$

问题：
1、两端的值饱和，梯度为接近0；
2、sigmoid的输出不是以 0 为中心的；梯度总是正或负的，也就是梯度只有一个更新方向。
3、exp()计算量大。

2. 双曲正切函数 tanh

$$\tanh x=\frac{\sinh x}{\cosh x}=\frac{e^x-e^{-x}}{e^x+e^{-x}}$$

特点:
1、压缩值在[-1,1];
2、以0为中心；
3、但存在值饱和，梯度为0情况。

3. 修正线性单元ReLu

$$relu(x)=max(x,0)$$
特点：
1、在正区域不存在饱和现象；
2、计算效率高；
3、比sigmoid，tanh收敛更快;
4、生物学中比sigmoid解释性更好;
5、但是结果不是以0为中心的；而且会导致Dead ReLU Problem(神经元坏死现象)：

ReLU在负数区域被kill的现象叫做dead relu。ReLU在训练的时很“脆弱”。在x<0时，梯度为0。这个神经元及之后的神经元梯度永远为0，不再对任何数据有所响应，导致相应参数永远不会被更新。

产生这种现象的两个原因：参数初始化问题；learning rate太高导致在训练过程中参数更新太大。

4. Leaky ReLu

$$LRelu(x)=max(0.01x,x)$$

5. PReLu

参数化的修正器Parametric Rectifier（PReLu）.

f ( y i ) = { y i ,  if  y i > 0 a i y i ,  if  y i ≤ 0 f\left(y_{i}\right)=\left\{

$$\begin{array}{ll} y_{i}, & \text { if } y_{i}>0 \\ a_{i} y_{i}, & \text { if } y_{i} \leq 0 \end{array}$$ \right. f(yi​)={yi​,ai​yi​,​ if yi​>0 if yi​≤0​

优化方法：
$$\frac{\partial \mathcal{E}}{\partial a_i}=\sum _{y_i}\frac{\partial \mathcal{E}}{\partial f\left(y_i\right)}\frac{\partial f\left(y_i\right)}{\partial a_i}$$

∂ f ( y i ) ∂ a i = { 0 ,  if  y i > 0 y i ,  if  y i ≤ 0 \frac{\partial f\left(y_{i}\right)}{\partial a_{i}}=\left\{

$$\begin{array}{ll} 0, & \text { if } y_{i}>0 \\ y_{i}, & \text { if } y_{i} \leq 0 \end{array}$$ \right. ∂ai​∂f(yi​)​={0,yi​,​ if yi​>0 if yi​≤0​

其中，$\mathcal{E}$代表目标函数。
动量方法更新：
$$\Delta a_i:=\mu \Delta a_i+ϵ\frac{\partial \mathcal{E}}{\partial a_i}$$

激活函数可以自适应地学习矫正线性单元的参数，并且能够在增加可忽略的额外计算成本下提高准确率。

6. Exponential Linear Units (ELU)

f ( x ) = { x  if  x > 0 α ( exp ⁡ ( x ) − 1 )  if  x ≤ 0 f(x)=\left\{

$$\begin{array}{ll} x & \text { if } x>0 \\ \alpha(\exp (x)-1) & \text { if } x \leq 0 \end{array}$$ \right. f(x)={xα(exp(x)−1)​ if x>0 if x≤0​

特点：
1、和Leaky ReLu相比，在负区有一点的鲁棒性。

7. Maxout

$$\max \left(w_1^{T}x+b_1,w_2^{T}x+b_2\right)$$

特点：
1、泛化的Relu 和Leaky ReLu;
2、但是引入了更多的参数。

总结：

• 使用 ReLu，注意学习率；
• 尝试 Leaky ReLU/Maxout/ELU;
• 尝试 tanh，但期望不要太高；
• 不要使用 sigmoid。

8. 比较sigmoid，tanh

import matplotlib.pyplot as plt
import numpy as np
exp = np.exp 

def sigmoid(x):
    return exp(x)/(1 + exp(x))

def tanh(x):
    return (exp(x) - exp(-x))/(exp(x) + exp(-x))
    
plt.subplot(2,1,1)
x = np.linspace(-10, 10, 1000)
sigmoid_x = sigmoid(x)
plt.plot(x, sigmoid_x)
plt.title("sigmoid")
plt.grid()

plt.subplot(2,1,2)
tanh_x = tanh(x)
plt.plot(x, tanh_x)
plt.title("tanh")
plt.grid()
plt.show()
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

结果：

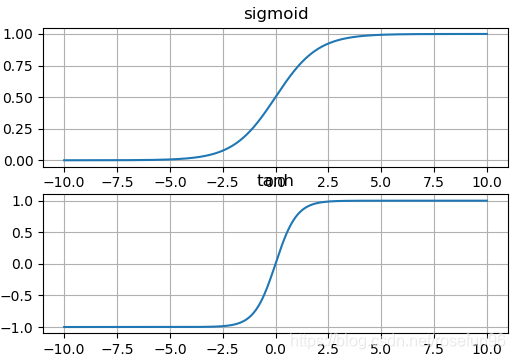
区别：
tanh 具有负值，对于一些不想出现负值的情况，多使用 sigmoid；tanh两端几乎没有梯度，比sigmoid的梯度还小。

---

参考：

1. tanh sigmoid 区别；
2. Delving Deep into Rectifiers:Surpassing Human-Level Performance on ImageNet Classification;
3. cs231n ppt;
4. 常见激活函数优缺点与dead relu problem