邻接表的最小生成树kruskal算法_对于下图中的网,写出该网的邻接链表;然后给出按kruskal算法得到的最小生成树。

作者：IT小白 | 2024-03-15 17:54:21

踩

对于下图中的网,写出该网的邻接链表;然后给出按kruskal算法得到的最小生成树。

###邻接表
####无向网节点定义

typedef struct ANode{
    int adjvex;
    struct ANode * nextarc;
    int info;                      
}ArcNode;
//边节点类型

typedef struct Vnode{
    char data;
    ArcNode *firstarc;
}VNode,AdjList[MAXV];
//表头结点信息

typedef struct {
    AdjList adjlist;                       
    int n,e;                                //顶点数，边数
}ALGraph;
//完整的图邻接表类型

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19

-节点的逻辑结构

[外链图片转存失败,源站可能有防盗链机制,建议将图片保存下来直接上传(img-Hvl0kcFt-1610420600360)(https://thumbnail0.baidupcs.com/thumbnail/a34b63534a4c5731fc375a2ced9c2606?fid=3712045569-250528-914935062880222&time=1512262800&rt=sh&sign=FDTAER-DCb740ccc5511e5e8fedcff06b081203-g3AcZxQysMKSclDCMnkRGanqcyc=&expires=8h&chkv=0&chkbd=0&chkpc=&dp-logid=7802409711651854039&dp-callid=0&size=c710_u400&quality=100&vuk=-&ft=video)]

###最小生成树Kruskal算法

生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树
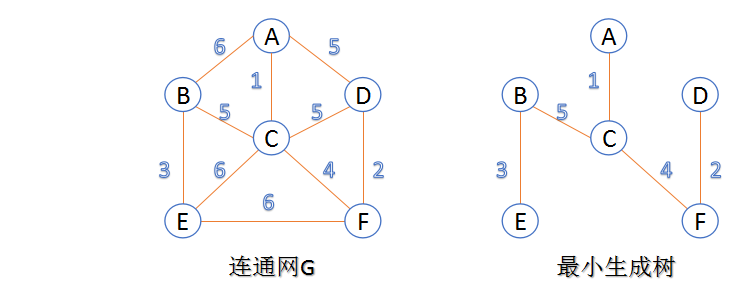
生成过程：

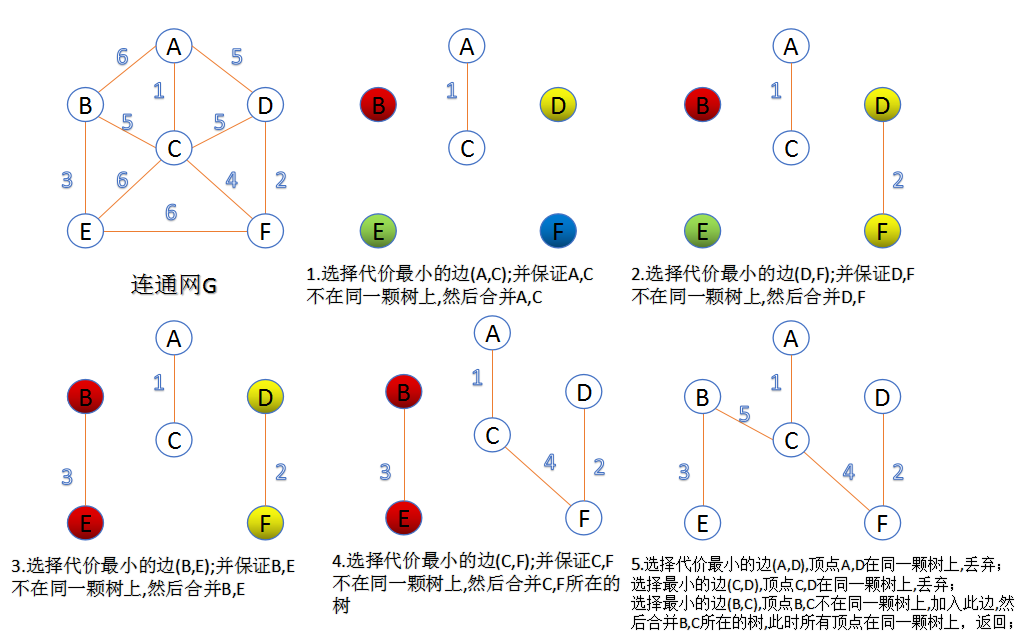
###在计算机储存结构中

邻接表G
最小生成树E的邻接表

####NULL表示指针为空，null表示权值为空（避免重复权值）

###代码解读
-创建连通网G

void CreateALGraph(ALGraph *G){
    int i,j,k,w;
    ArcNode *p;
    printf("请输入顶点数和边数\n");
    scanf("%d,%d",&G->n,&G->e);
    for (i=0; i < G->n;i++) {
        printf("请输入顶点信息\n");
        scanf("%s",&G->adjlist[i].data);
        G->adjlist[i].firstarc=NULL;
    }
    
    for (k=0; k<G->e; k++) {
        printf("输入第%d条边的两顶点编号和权值:",k+1);
        scanf("%d,%d,%d",&i,&j,&w);             //顶点编号0，顶点编号1，两者的权值
        
        p=(ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex=j;
        p->info = w;
        p->nextarc=G->adjlist[i].firstarc;
        G->adjlist[i].firstarc=p;
        
        p=(ArcNode *)malloc(sizeof(ArcNode));
        p->adjvex=i;
        p->info =NULL;
        p->nextarc=G->adjlist[j].firstarc;
        G->adjlist[j].firstarc=p;
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29

-最小生成树E

void CreateKruskal(ALGraph *G,ALGraph *E){
    int i ,j=0;
    int bj[MAXV];
    int a[MAXV],b[MAXV]; //a里面放权值，b里放相应权值对应的顶点行（减少遍历次数，提高效率）
    int min,min_dex,ls;//连锁标记
    int result=0;
    E->n=G->n;
    E->e=G->e;
    ArcNode *p;
    ArcNode *q;
    for (i=0; i<G->n; i++) {   //循环顶点 a,b,c,d,e,f
        for (p=G->adjlist[i].firstarc; p!=NULL; p=p->nextarc){
            if (p->info!=NULL) {
                a[j]=p->info;
                b[j]=i;
                j++;
            }
            
        }
    }                       //a,b 创建好，j中是权值个数
    for (i=0; i<G->n; i++) {
        bj[i]=i;
    }//建立bj[]标记表（不同标记，代表不同的树）
    while(result==0){
        min=a[0];
        min_dex=0;
        for (i=1; i<j; i++) {
            if (a[i]< min) {
                min=a[i];
                min_dex=i;
            }
        }
        a[min_dex]=a[j-1]+1;  //去掉最小值（把当前拿出的最小值变成 最大值+1）
        for (p=G->adjlist[b[min_dex]].firstarc; p!=NULL; p=p->nextarc){
            if (p->info==min) {
                if (bj[b[min_dex]] != bj[p->adjvex]) {
                    ls=bj[p->adjvex];
                    for (i=0; i<G->n; i++) {  //这个循环解决当标记表为{0，0，1，1}时,连接一个0和1,自动把剩下的1变为0,【达到连接两个树的目的】 
                        if (bj[i]==ls) {
                            bj[i]=bj[b[min_dex]];
                        }
                    }
                    q=(ArcNode *)malloc(sizeof(ArcNode));
                    q->adjvex=p->adjvex;
                    q->info=p->info;
                    q->nextarc=E->adjlist[b[min_dex]].firstarc;
                    E->adjlist[b[min_dex]].firstarc = q;
                }
            }//在a中找最小值，通过下标，在b中找哪一行顶点，判断p->info是否与最小值相等，相等就把adjvex 顶点信息  判断加入到E中
        result=1;
        for(i = 0; i<G->n; i++){
            if(a[0] != a[i])
            {
                result=0;
                break;
            }
        }//   如果标记数组全部相等（成一颗树） 则循环结束
    }
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60

本算法通过把邻接表G中每条边权值读入a[]数组中，（通过b[]数组记录权值读入时的顶点行，提高搜索效率）。
然后从a中拿最小权值，在G指定顶点行中查找，如果找到边节点，则判断该边节点顶点与头结点顶点是否属于同一颗树（看BJ[] 标记表数是否一样）
如果不一样就加入到E邻接表中，并将等于边节点标记数全部改为头结点标记数
如果一样就不加入到E表中
最后判断标记表是否是一棵树（标记表全相等）
如果不等，进入下一次循环，又在a[]数组中找最小值拿入
如果相等，结束循环

a[]={1,2,3,4,5,5,5,6,6,6}
bj[]={ 0, 1, 2, 3, 4, 5 } 相当于5颗树
对应 =A·B··C··D··E···F

第一次循环从a中拿出权值1，并在顶点A,C中找到，加入E后，bj[]={0,1,0,3,4,5}
第二次循环从a中拿出权值2，并在顶点D,F中找到，加入E后，bj[]={0,1,0,3,4,3}
第三次循环从a中拿出权值3，并在顶点B,E中找到，加入E后，bj[]={0,1,0,3,1,3}
第四次循环从a中拿出权值4，并在顶点C,F中找到，加入E后，bj[]={0,1,0,0,1,0}
第五次循环从a中拿出权值5，当在顶点A,D中找到时，因为A,D的标记均为0，表示在一颗树上，所以不放入E
第六次循环从a中拿出权值5，当在顶点B,C中找到时，因为B,C标记为1，0 不在同一颗树上，所以放入E，此时bj[]={0,0,0,0,0}
循环结束，打印结果

打印代码与main函数如下

void DispALGraph(ALGraph *G){
    int i,max=0,max_index=0;
    ArcNode *p;
    printf("图的邻接表如下:\n");
    printf("编号     顶点   相邻编号，权值\n");
    for (i=0; i<G->n; i++) {
        int j=0;
        printf("%4d %8c",i,G->adjlist[i].data);
        for (p=G->adjlist[i].firstarc; p!=NULL; p=p->nextarc) {
            printf(" --> ");
            printf("%d,%d",p->adjvex,p->info);
            j++;
            if (max<j) {
                max=j;
                max_index=i;
            }
        }
        printf("\t该顶点有%d个边\n",j);
    }
    printf("    编号%d有最多度\n",max_index);
    
}


int main(){
    ALGraph G;          //无向网连通网G
    ALGraph E;          //最小生成树
    CreateALGraph(&G);  //在每个头结点后面加上边的信息
    DispALGraph(&G);    //打印无向网
    CreateKruskal(&G,&E);//创建最小生成树
    DispALGraph(&E);//打印最小生成树
    return 0;
}
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33

输入输出结果如下
在这里插入图片描述

其中两个生成树图来自

http://blog.csdn.net/luoshixian099/article/details/51908175

本文内容由网友自发贡献，转载请注明出处：【wpsshop博客】