概率题智力题_某城市发生了一起汽车撞人逃跑事件,该城市只有两种颜色的车,蓝15%绿85%,事发时有

---

概率题

面试常见智力题和概率题目及部分答案

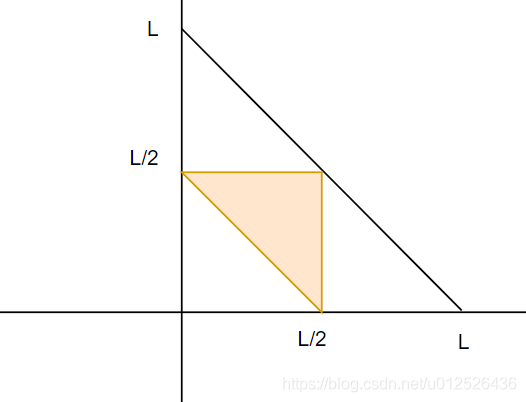
1. 1段1米长的绳子，随机切两刀，分成三段，求能够组合成一个三角形的概率？

2. 两个人轮流抛硬币，正面获胜，先抛的人获胜的概率

A先，B后

P(A) = 1/2 +      //A直接取胜 
	   1/2 * 1/2 * 1/2 +      // A1失败B1失败A2取胜
	   1/2 * 1/2 * 1/2 * 1/2 *1/2  +    //A1失败B1失败A2失败B2失败A3取胜
	   ...

p = 1/2 + (1/2)^3 + (1/2)^5 + (1/2)^7 + ...
等比数列求和
p = 1/2 * (1 - (1/4)^n) / (1 - 1/4) = 2/3




P(B） = 1/2 * 1/2 +     // A1失败B1取胜
        1/2 * 1/2 * 1/2 * 1/2 +     // A1失败B1失败A2失败B2取胜
        1/2 * 1/2 * 1/2 * 1/2 * 1/2 * 1/2 +  //A1失败B1失败A2失败B2失败A3失败B3取胜、
        ...    
p = (1/2)^2 + (1/2)^4 + (1/2)^6 + ..

p = 1/4 * (1 - (1/4)^n) / (1 - 1/4)
		

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23

3. 如果在高速公路上30分钟内到一辆车开过的几率是0.95，那么在10分钟内看到一辆车开过的几率是多少？

4. 一个硬币抛了10次，8次为正，2次为反，求第11次抛硬币为正的概率

假设硬币为正面的概率为p

极大似然估计求解

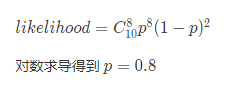
最大后验估计求解

5. 有8个箱子，现在有一封信，这封信放在这8个箱子中（任意一个）的概率为4/5,不放的概率为1/5（比如忘记了）,现在我打开1号箱子发现是空的，求下面7个箱子中含有这封信的概率为？

实际上问题是条件概率问题，首先*放在每个抽屉里的概率都是(1-1/5)1/8=1/10：

**记A={第一个抽屉里没有} B={其余7个里面有}，**则问题是求P(B|A)

P(B|A)=P(AB)/P(A) (条件概率公式)

P(AB)=(1-1/5)*(1-1/8)=7/10 其中1-1/5指的是放在抽屉里，1-1/8指的是不放在第一个里面

P(A)=1-1/10=9/10 二者相比有P(B|A)=7/9

6. 一对夫妻有2个孩子，求一个孩子是女孩的情况下，另一个孩子也是女孩的概率

7. 袋中装有m枚正品硬币、n枚次品硬币（次品硬币两面均印有国徽）。从袋中任取一枚硬币,将它投掷r次，已知每次均出现国徽，问这枚硬币是正品硬币的概率是多少?

8. 从一副52张扑克牌中随机抽两张，颜色相等的概率

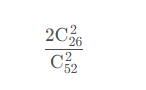
9. 54张牌，分成6份，每份9张牌，大小王在一起的概率

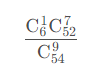
10. 52张牌去掉大小王，分成26*2两堆，从其中一堆取4张牌为4个a的概率

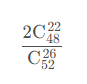
11. 某城市发生了一起汽车撞人逃跑事件，该城市只有两种颜色的车，蓝色15%，绿色85%，事发时有一个人在现场看见了，他指证是蓝车。但是根据专家在现场分析,当时那种条件能看正确的可能性是80%。那么,肇事的车是蓝车的概率到底是多少？

12. 在一个重男轻女的国家里，每个家庭都想生男孩，如果他们生的孩子是女孩，就再生一个，直到生下的是男孩为止。这样的国家，男女比例会是多少？

答案：

1:1

分析：

每个孩子出生男女概率是50%，所以每次出生的男女比例是相同的。

假设这个国家有n对夫妇，那么n对夫妇将生下n个男孩，这n个男孩是这样生下的，假设生男生女的概率是50%，那么n/2个男孩是第一胎生下的，同时将有n/2个女孩生下，n/2对生女孩的夫妇将继续生，其中n/4的夫妇生下男孩，n/4的夫妇继续生下女孩，然后是n/8的夫妇顺利得到男孩，又有n/8的夫妇生下女孩，依此类推，这个国家将生下n/2 + n/4 + n/8 + …的女孩，所以男女比例是n : (n/2 + n/4 + n/8+ …) = n : n = 1 : 1

智力题

面试真题：经典智力题最详汇总（上）

面试真题：经典智力题最详汇总（中）

面试真题：经典智力题最详汇总（下）

1. 烧绳计时问题

问题： 烧一根不均匀的绳，从头烧到尾总共需要1个小时。现在有若干条材质相同的绳子，问如何用烧绳的方法来计时一个小时十五分钟呢？
解答：

1. 先把1根绳子从两头点燃,燃烧完毕后刚好30分钟。
2. 在第1根绳子点燃的同时,从一头点燃第2根,那么在第1根燃烧完毕后(30分钟),再把第2根绳子未点燃的那一头点燃,燃烧完毕后用去了45分钟(30+15)。
3. 在第2根绳子燃烧完毕后,从两头点燃第3根绳子,等第3根燃烧完毕后,刚好1小时15分钟(45+30)。

step 1：将一根完整的绳子A两端同时开始烧，另一根完整的绳子B一端开始烧；

step 2：当A烧完的时候(30分钟)，我们再将B的另一端点燃，即对一根30分钟的绳子两端同时烧；

step 3：当B烧完的时候(30 + 15)，我们得到了45分钟；

step 4：再如同1，我们再从两端同时开始烧一跟绳子C，烧完时候即又过去30分钟，所有总共得到：30 + 15 + 30 = 1小时15分钟

2. 2个鸡蛋 100层楼问题

题目描述：

一道非常经典的面试题目，给你两个鸡蛋，在一幢100层的大楼里面，至少扔几次可以测出让鸡蛋破碎的临界高度？

两个软硬程度一样但未知的鸡蛋，它们有可能都在一楼就摔碎，也可能从一百层楼摔下来没事。

有座100层的建筑，要你用这两个鸡蛋确定哪一层是鸡蛋可以安全落下的最高位置。可以摔碎两个鸡蛋。

最少需要几次测试，才能得到摔碎鸡蛋的楼层？方案如何？

=================================================

对于这个问题，如果从编程角度而言，最简单的思路是用动态规划的思想来解决，不过本文不将其从编程角度分析，而是从数学角度对问题进行论述。

================================================

对这个问题，原始问题——【100层楼，最少需要几次测试，才能得到摔碎鸡蛋的楼层】，直接考虑不容易考虑，但是，如果将这个问题进行一种等价的转换，这个问题将会变得非常容易解答。个人认为，这个转换是解决这个问题的核心，这个转换是：

转换问题——【两个鸡蛋，进行k次测试，最多可以测试几层楼】

如果大家能想到将“原始问题”变为“转换问题”，这个问题个人认为已经解决一半了，转换后，这个问题豁然开朗，思路全开。

现在我们以“转换问题”为模板进行考虑，有两个鸡蛋，第一个鸡蛋如果破碎，第二个鸡蛋就必须只能一层一层的测试了，而且，我们要求进行k次测试就将摔碎鸡蛋的楼层必须找到.

=====================================================

考虑第一次测试。第一次测试的时候，第一个鸡蛋不能放置的楼层太高了，否则，如果第一个鸡蛋破碎，第二个鸡蛋可能不能在k次测试后得到结果。但是也不能放置的矮了，因为如果放置的矮了，第一个鸡蛋破碎了还好说，如果没破，我们浪费了一次测试机会，也不能说是完全浪费了，不过至少是让效用没有最大化。所以，第一次测试的时候必须让第一个鸡蛋放置的不高不矮。

不高不矮是多高？高到如果第一个鸡蛋破碎后第二个鸡蛋刚好能完成k次测试得到结果这个目标。由此可知，第一次测试所在的楼层高度为k，如果第一次测试第一枚鸡蛋破碎，则剩下k-1层楼，一层一层的试，k次一定能完成目标。

如果第一次测试，第一枚鸡蛋没有破碎，则我们现在只有k-1次测试机会了，而且直到了k楼及其以下都是安全的了。我们消耗了一次测试机会，但是一次就测试了k层楼。

然后只有k-1次机会了，第二次测试，我们可以在k层的基础上再增加k-1层了，注意，这个时候由于我们只有k-1次机会，所以这次只能再增加k-1层，以保证测试的时候第一枚鸡蛋破碎的情况下仍然能完成任务。

于是，重复上述过程，直到最后一次机会，我们总共测试的楼层数为：

k+(k-1)+(k-2)+(k-3)+…+1

然后，再回到“原始问题”，100层楼，如果需要k次测试才能测试完成，则必须有

k+(k-1)+(k-2)+(k-3)+…+1 = k(k+1)/2 >=100

则可以得到，k≥14

也就是需要14次测试才能得到结果，而且这个过程也将测试方案一并得出来，就是第一次在14楼测试，如果第一枚蛋碎，则剩余13次机会，13层未知楼层，恰好，第二次在14+13=27楼测试，如此。

3. 用多少个乒乓球能装满这间屋子？

【参考答案】

房间体积=1个乒乓球的体积 * 乒乓球个数

所以，乒乓球个数=房间体积 / 1个乒乓球的体积，从而将一个复杂问题拆解为两个子问题：

1）房间体积

2）1个乒乓球的体积

1）房间体积

这间房子大概长是x米，宽x米，高x米，能得出这个屋子的体积

2）1个乒乓球的体积

一个乒乓球的直径大概是x厘米，就能得出一个乒乓球的大概体积=直径直径 直径。

然后用估算的1）房间的体积 除以 2）1个乒乓球的体积，就能算出这间屋子大概能装下多少乒乓球

经典面试题“费米问题”如何回答？有哪些比较好的案例？