第1关：顺序表的插入操作

任务描述

本关任务：编写顺序表的初始化、插入、遍历三个基本操作函数。

相关知识

顺序表的存储结构

顺序表的存储结构可以借助于高级程序设计语言中的数组来表示，一维数组的下标与元素在线性表中的序号相对应。线性表的顺序存储结构可用C语言中动态分配的一维数组定义如下：

1. /*线性表的动态分配顺序存储结构（用一维数组）*/
2. #define INIT_SIZE 100 //线性表存储空间的初始分配量
3. #define INCREMENT 10 //线性表存储空间的分配增量
4. typedef struct
5. {
6. ElemType *elem; //存储空间基地址
7. int length; //当前长度
8. int listsize; //当前分配的存储容量
9. }SqList;

在上述定义中，ElemType为顺序表中数据元素的类型，SqList是顺序表类型。

为了令算法具有通用性，使其尽可能地适用于各种可能的场合，将要处理的数据类型加以抽象，使其适用于不同类型的数据，是提高代码通用性的重要手段。

ElemType类型根据实际问题需要灵活定义：

1. /* 定义ElemType为int类型 */
2. typedef int ElemType;

或者，有学生数据类型定义如下：

1. typedef struct date
2. { int year;
3. int month;
4. int day;
5. }DATE;
6. typedef struct student
7. {
8. int num;
9. char name[20];
10. char sex;
11. DATE birthday;
12. float score;
13. }STUDENT;

1. /* 定义ElemType为STUDENT类型 */
2. typedef STUDENT ElemType;

顺序表中数据类型ElemType可以多种多样，但是在编程实现算法时针对不同数据类型，每类数据元素的输入输出是有区别的，顺序表的基本操作算法要在计算机上执行，须针对ElemType类型数据编写输入、输出、比较等函数：

1. void input(ElemType &s);
2. void output(ElemType s);
3. int equals(ElemType a,ElemType b);

C语言函数基本的参数传递机制是值传递，被调函数对形式参数的任何操作都是作为局部变量进行，不会影响主调函数的实参变量的值。如果需要将函数中变化的形式参数的值反映在实际参数中，在C语言的实现中，就需要通过指针变量作形式参数，接收变量的地址，达到修改实参变量值的目的。

C++语言中用引用作函数的形参，被调函数对形参做的任何操作都影响了主调函数中的实参变量值，而操作一个变量比操作一个指针要简单的多，为了便于算法描述，本书函数参数传递机制采用有两种方式：值传递和引用传递。如果不想修改实参的值，函数参数传递按值传递；如果需要修改实参的值，则使用引用传递。

举例说明，在定义输入函数void input(ElemType &s);时，在函数体内需要输入主调函数中的实参变量的值，也就是说要改变主调函数中的实参变量的值，因此函数形参定义为引用；在定义输出函数void output(ElemType s);时，在函数体内不需要改变主调函数中的实参变量的值，只需读取主调函数中的实参变量的值，因此函数形参定义为变量，采用值传递。

顺序表的初始化操作、销毁操作、插入操作和删除操作，在函数体内改变了顺序表L的数据成员的值，因此函数形参为引用。顺序表的查找操作、遍历操作，在函数体内不改变顺序表L的数据成员的值，函数形参为变量，采用值传递。

下面举例说明如何在线性表的顺序存储结构上实现线性表的基本操作。

顺序表的初始化操作

1. void InitList(SqList&L)
2. { // 操作结果：构造一个空的顺序线性表L
3. L.elem=(ElemType*)malloc( INIT_SIZE*sizeof(ElemType));
4. if(!L.elem)
5. exit(-1); // 存储分配失败
6. L.length=0; // 空表长度为0
7. L.listsize=INIT_SIZE; // 初始存储容量
8. }

顺序表的遍历操作

1. void ListTraverse(SqList L,void(*vi)(ElemType ))
2. { // 初始条件：顺序线性表L已存在
3. // 操作结果：依次对L的每个数据元素调用函数vi()
4. ElemType *p;
5. int i;
6. p=L.elem;
7. for(i=1; i<=L.length; i++)
8. vi(*p++);
9. printf("\n");
10. }

在执行ListTraverse()函数输出顺序表的所有数据元素时，用函数指针vi来实现对output()函数的调用。

在执行遍历函数输出顺序表的所有数据元素时，用函数指针vi来实现对output()函数的调用。

顺序表的插入运算

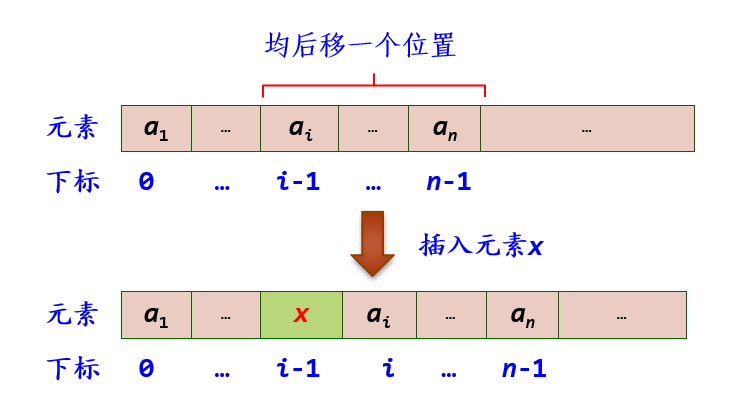
线性表的插入运算是指在表的第i (1≤i≤n+1)个位置，插入一个新元素x，使长度为n的线性表 ( a1​，…，ai−1​，ai​，…，an​) 变成长度为n+1的线性表( a1​，…，ai−1​，x，ai+1​，…，an​) 。

算法思想：用顺序表作为线性表的存储结构时，由于结点的物理顺序必须和结点的逻辑顺序保持一致，因此我们必须将原表中位置n-1，n-2，…，i-1上的结点，依次后移到位置n，n-1，…，i上，空出第i-1个位置，然后在该位置上插入新结点x。当i=n+1时，是指在线性表的末尾插入结点，所以无需移动结点，直接将x插入表的末尾即可。

算法分析：

1. 最好的情况：当i=n+1时（插入尾元素），移动次数为0；
2. 最坏的情况：当i=1时（插入第一个元素），移动次数为n；
3. 平均情况：在位置i插入新元素x，需要将ai～an的元素均后移一次，移动次数为n-i+1。假设在等概率下pi（pi=1/(n+1)），移动元素的平均次数为：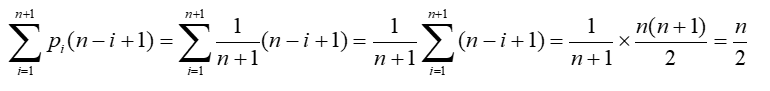 

   

插入算法的主要时间花费在元素移动上，所以算法平均时间复杂度为O(n)。

编程要求

根据提示，在右侧编辑器 Begin-End 区间补充代码，完成顺序表的初始化操作，遍历操作及插入操作三个子函数的定义，具体要求如下：

• void InitList(SqList &L); //构造一个空的顺序表L
• void ListTraverse(SqList L,void(*vi)(ElemType ));// 依次调用函数vi()输出顺序表L的每个数据元素
• int ListInsert(SqList &L,int i,ElemType e);//在顺序表L中第i个位置之前插入新的数据元素

测试说明

平台会对你编写的代码进行测试：

输入说明 第一行输入顺序表的长度M； 第二行输入顺序表的M个整数； 第三行输入要插入元素的位置； 第四行输入要插入的数据元素的值。

输出说明 第一行输出插入是否成功的提示信息； 如果插入成功，第二行输出插入元素后的顺序表所有元素；如果插入失败，则不输出第二行。

测试输入： 5 12 47 5 8 69 1 99 预期输出： 插入成功，插入后顺序表如下： 99 12 47 5 8 69

测试输入： 5 12 47 5 8 69 7 99 预期输出： 插入位置不合法，插入失败！

---

核心代码

void InitList(SqList&L) {
    int MAXSIZE=100;
    L.elem=new ElemType[MAXSIZE];
    if(!L.elem) exit(0);
    L.length=0;
    L.listsize=MAXSIZE;
}
int  ListInsert(SqList &L,int i,ElemType e)
{   // 初始条件：顺序线性表L已存在，1≤i≤ListLength(L)+1
    // 操作结果：在L中第i个位置之前插入新的数据元素e，L的长度加1
    /********** Begin **********/ 
    if((i<1)||(i>L.length+1))  return 0;
    if(L.length==MAXSIZE)  return 0;
    for(int j=L.length-1;j>=i-1;j--)
    {
        L.elem[j+1]=L.elem[j];
    }
    L.elem[i-1]=e;
    ++L.length;
    return 1;
    
    /********** End **********/
}
void ListTraverse(SqList L)
{   // 初始条件：顺序线性表L已存在
    // 操作结果：依次对L的每个数据元素调用函数vi()输出  
    /********** Begin **********/ 
    for(int i=0;i<L.length;i++)
    {
        cout<<L.elem[i]<<" ";
    }
    /********** End **********/
}