devbox
Guff_9hys
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

Java实现红黑树数据结构_java红黑树数据结构

作者：Guff_9hys | 2024-06-22 16:03:16

赞

踩

java红黑树数据结构

红黑树

红黑树的概述

红黑树的特性

  1. 所有节点都有两种颜色:红与黑
  2. 所有的null节点视为黑色
  3. 红色节点之间不能相邻
  4. 根节点是黑色
  5. 从根到任意一个叶子节点,路径中的黑色节点数也一样(黑色完美平衡)

这里给大家解释一下叶子节点其实就是二叉树节点的最后一层,简单理解起来的话确实是这样

判断是否是红黑树

很明显上图不是一个红黑树,违反了规则3,红色节点不能相邻

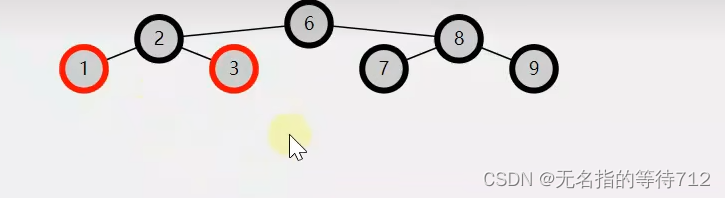
很明显上图也不是一个红黑树,违反了规定5,从根节点到任意一个叶子节点路径中的黑色节点数一样,可以看出来1和3的黑色节点只有6和2,但是7的节点却有6,8,7三个数,9的节点也有三个数6,8,9，故而不满足红黑树条件

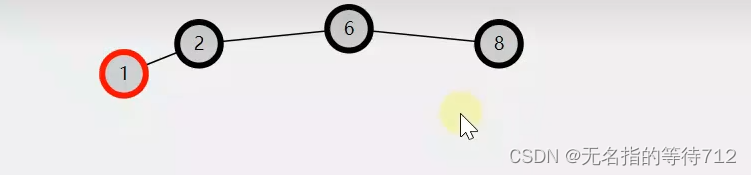
上图就是一个红黑树了,1到根节点的黑色节点有两个,8到根节点的黑色节点也是有两个

上面这个图就有一定的迷惑性了,看着的话像一个红黑树,其条件也确实满足,但是没有考虑到一件事情,那就是null节点,条件2明确说了所有的null节点视为黑色,所以上图又可以变换为下面的图片

从此图就可以看出来1下面的叶子节点就是一个很明显的错误,与8下面的叶子节点到根节点的数量不符合.

下面就得出一个重要结论:红色的叶子节点可以单独出现,可以在左侧叶子节点,也可以在右侧的叶子节点,但是黑色的叶子节点就必须成对出现,否则就需要考虑条件2

红黑树基础代码

  1. public class RedBlackTree {
  2.  
  3.     //枚举
  4.     enum Color {
  5.         RED,BLACK;
  6.     }
  7.     //根节点
  8.     private Node root;
  9.  
  10.     //红黑树节点
  11.     private static class Node {
  12.         int key;
  13.         Object value;
  14.         Node left;
  15.         Node right;
  16.         Node parent;    //父节点
  17.         Color color;
  18.  
  19.         //判断当前节点是否是左孩子
  20.         boolean isLeftChild(){
  21.             //如果父节点都为null的话,根本就不可能会有左孩子,同样如果父节点的左孩子不是当前节点的话也可以判断当前节点不是左孩子
  22.             return parent != null && parent.left == this;
  23.         }
  24.  
  25.         //返回当前节点的叔叔节点
  26.         Node uncle(){
  27.             //判断如果当前节点的父节点和爷爷节点有一个为null的话,就可以判断当前节点并没有叔叔节点
  28.             if(parent == null || parent.parent == null){
  29.                 return null;
  30.             }
  31.             //判断父节点是否是爷爷节点的左孩子,如果是返回爷爷节点的右孩子
  32.             if(parent.isLeftChild()){
  33.                 return parent.parent.right;
  34.             }else{
  35.                 return parent.parent.left;
  36.             }
  37.         }
  38.  
  39.         //返回当前的兄弟节点
  40.         Node sibling(){
  41.             //判断当前节点的父节点如果为null了的话,就不会有兄弟节点了
  42.             if(parent == null){
  43.                 return null;
  44.             }
  45.             //判断如果当前节点是父节点的左孩子,则返回右节点,反之返回左节点
  46.             if(this.isLeftChild()){
  47.                 return parent.right;
  48.             }else{
  49.                 return parent.left;
  50.             }
  51.         }
  52.     }
  53.  
  54.     //判断当前节点是否是红色
  55.     boolean isRed(Node node){
  56.         //判断如果当前节点不为null，并且当前节点的颜色等于红色的时候才是红色节点
  57.         return node != null && node.color == Color.RED;
  58.     }
  59.  
  60.     //判断当前节点是否是黑色节点
  61.     boolean isBlack(Node node){
  62.         //如果不是红色节点就是黑色节点
  63.         return !isRed(node);
  64.     }
  65. }

右旋

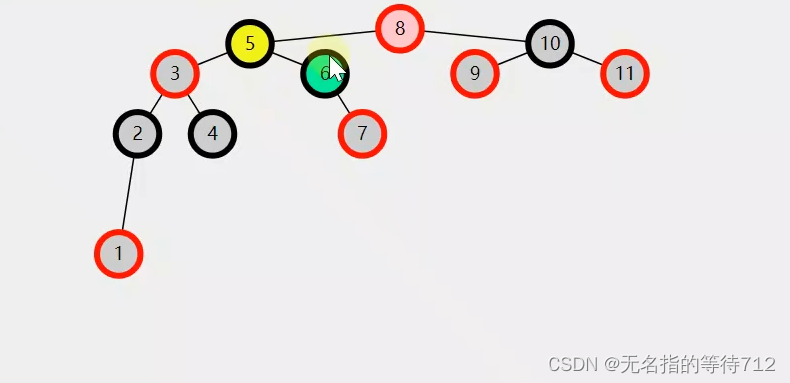
可以由上图看出要旋转的节点是8（粉色）,5（黄色）是8粉色节点的左孩子,6（绿色）是黄色节点的右孩子

旋转之后

  1. /**
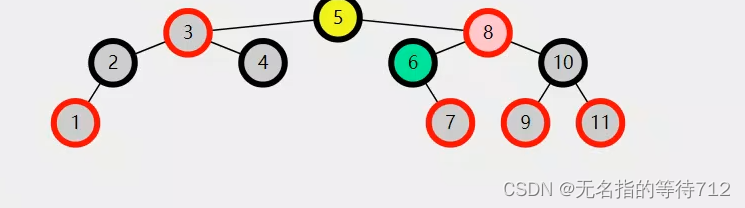
  2.      * 右旋函数
  3.      *  1.对于parent的处理
  4.      *  2.旋转后行嗯的父子关系
  5.      * @param pink
  6.      */
  7.     private void  rightRotate(Node pink){
  8.         //找到粉色节点的父节点
  9.         Node parent = pink.parent;
  10.         //pink节点的左孩子是yellow节点
  11.         Node yellow = pink.left;
  12.         //green节点是yellow节点的右侧孩子
  13.         Node green = yellow.right;
  14.         //判断当前绿色节点不为null的话,绿色节点的父节点就应该等于粉色节点
  15.         if(green != null){
  16.             green.parent = pink;
  17.         }
  18.         //旋转之后让黄色节点的右孩子等于粉色节点
  19.         yellow.right = pink;
  20.         //旋转之后黄色节点的父节点等于粉色节点的父节点
  21.         yellow.parent = pink.parent;
  22.         //旋转之后粉色节点的左孩子等于绿色节点
  23.         pink.left = green;
  24.         //旋转之后粉色节点的父节点等于黄色节点
  25.         pink.parent = yellow;
  26.         //判断如果粉色节点的父节点为null的话,根节点就变为黄色节点
  27.         if(parent == null ){
  28.             root = yellow;
  29.         }
  30.         //如果父节点的左孩子是粉色节点的话
  31.         else if(parent.left == pink){
  32.             //父节点的左孩子就等于黄色节点
  33.             parent.left = yellow;
  34.         }else{
  35.             //父节点的右孩子就等于黄色节点
  36.             parent.right = yellow;
  37.         }
  38.     }

左旋

  1. /**
  2.      * 左旋函数
  3.      *
  4.      * @param pink
  5.      */
  6.     private void leftRotate(Node pink) {
  7.         // 找到粉色节点的父节点
  8.         Node parent = pink.parent;
  9.         // 粉色节点的右孩子是黄色节点
  10.         Node yellow = pink.right;
  11.         // 绿色节点是黄色节点的左侧孩子
  12.         Node green = yellow.left;
  13.         // 如果绿色节点不为null，将绿色节点的父节点设为粉色节点
  14.         if (green != null) {
  15.             green.parent = pink;
  16.         }
  17.         // 旋转后，将黄色节点的左孩子设为粉色节点
  18.         yellow.left = pink;
  19.         // 将黄色节点的父节点设为粉色节点的父节点
  20.         yellow.parent = pink.parent;
  21.         // 旋转后，将粉色节点的右孩子设为绿色节点
  22.         pink.right = green;
  23.         // 将粉色节点的父节点设为黄色节点
  24.         pink.parent = yellow;
  25.         // 如果粉色节点的父节点为null，将黄色节点设为新的根节点
  26.         if (parent == null) {
  27.             root = yellow;
  28.         }
  29.         // 如果粉色节点是其父节点的左孩子，更新父节点的左孩子为黄色节点
  30.         else if (parent.left == pink) {
  31.             parent.left = yellow;
  32.         }
  33.         // 如果粉色节点是其父节点的右孩子，更新父节点的右孩子为黄色节点
  34.         else {
  35.             parent.right = yellow;
  36.         }
  37.     }

新增

  1. /**
  2.      * 新增或者更新
  3.      * 正常增,遇到红红不平衡进行调整
  4.      * @param key
  5.      * @param value
  6.      */
  7.     public void put(int key,Object value){
  8.         Node p = this.root;
  9.         Node parent = null;//设置父节点为null
  10.         while ( p!= null){
  11.             parent = p;//将父节点跟新为当前节点
  12.             if(p.key > key){
  13.                 p = p.left;
  14.             }else if(p.key < key){
  15.                 p = p.right;
  16.             }else{
  17.                 p.value = value;   //跟新的逻辑
  18.                 return;
  19.             }
  20.         }
  21.         //创建出来的需要添加的节点
  22.         Node inserted = new Node(key, value);
  23.         //判断如果父节点为null的话,根节点就是此时需要添加的节点
  24.         if(parent == null){
  25.             root = inserted;
  26.         }
  27.         //如果key比父节点的key还小的话,父节点的左孩子就是添加的节点
  28.         else if(key < parent.key){
  29.             parent.left = inserted;
  30.         }else
  31.         //如果key比父节点的key大的话,父节点的右孩子就是添加的节点
  32.         {
  33.             parent.right = inserted;
  34.         }
  35.     }

写道如上代码,普通的二叉树添加就完成了，但是此时还需要遇到红红不平衡的时候进行调整

但是此时就遇到了下面这种情况

  1. /**
  2.      * 新增或者更新
  3.      * 正常增,遇到红红不平衡进行调整
  4.      * @param key
  5.      * @param value
  6.      */
  7.     public void put(int key,Object value){
  8.         Node p = this.root;
  9.         Node parent = null;//设置父节点为null
  10.         while ( p!= null){
  11.             parent = p;//将父节点跟新为当前节点
  12.             if(p.key > key){
  13.                 p = p.left;
  14.             }else if(p.key < key){
  15.                 p = p.right;
  16.             }else{
  17.                 p.value = value;   //跟新的逻辑
  18.                 return;
  19.             }
  20.         }
  21.         //创建出来的需要添加的节点
  22.         Node inserted = new Node(key, value);
  23.         //判断如果父节点为null的话,根节点就是此时需要添加的节点
  24.         if(parent == null){
  25.             root = inserted;
  26.         }
  27.         //如果key比父节点的key还小的话,父节点的左孩子就是添加的节点
  28.         else if(key < parent.key){
  29.             parent.left = inserted;
  30.             //设置此时添加节点的父节点就是上面设置好的父节点
  31.             inserted.parent = parent;
  32.         }else
  33.         //如果key比父节点的key大的话,父节点的右孩子就是添加的节点
  34.         {
  35.             parent.right = inserted;
  36.             //设置此时添加节点的父节点就是上面设置好的父节点
  37.             inserted.parent = parent;
  38.         }
  39.         //遇到红红不平衡进行调整
  40.         fixRedRed(inserted);
  41.     }
  42.  
  43.     /**
  44.      * 遇到红红不平衡的进行调整
  45.      * @param x
  46.      */
  47.     private void fixRedRed(Node x){
  48.         //1.判断如果插入节点为根节点的话,直接变黑即可
  49.         if(x == root){
  50.             x.color = Color.BLACK;
  51.             return;
  52.         }
  53.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  54.         if(isBlack(x.parent)){
  55.             return;
  56.         }
  57.         
  58.     }

上述代码完成了条件1,条件2,接下来需要完成条件3了

条件3

可以看的出来上树是平衡的

第一步:此时添加1,就可以得到下图

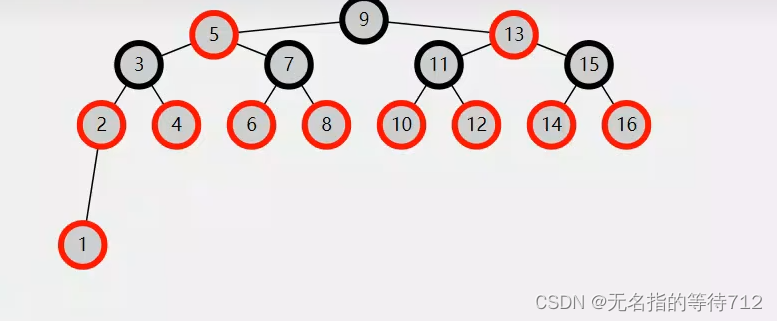
当时上面的图添加之后1节点和2节点违反了条件3

第二步:违反条件3之后,此时最好的解决办法就是把2节点换成黑色

但是此时1的叔叔节点4又不满足条件5了

第三步:此时最好的解决办法就是将叔叔节点4,也变为黑色

但是此时对于1这个叶子节点,和6，8，10，12，14，16这个节点违反了条件5

第四步:此时的解决办法只能是将3载设置为红色节点

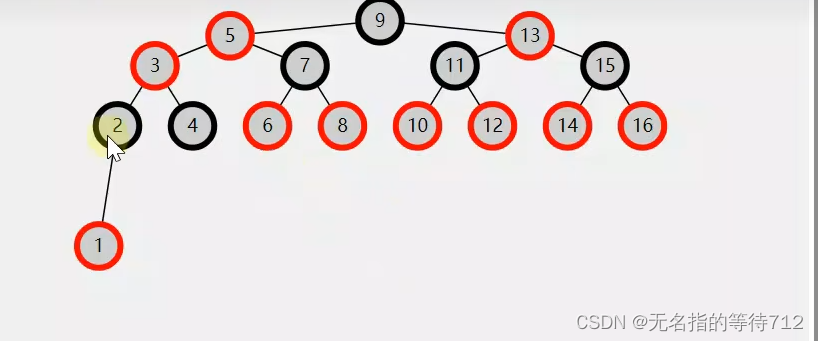
满足条件5之后又不满足条件3了

第五步:此时就可以递归了,将父亲节点变为黑色,叔叔节点也变为黑色

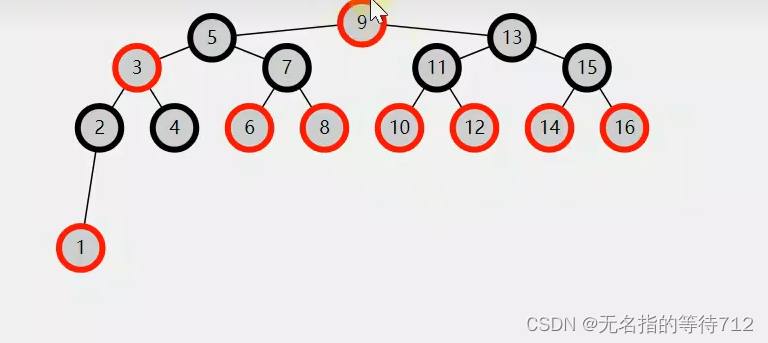
此时不满足条件4了,所以直接将9这个节点变为黑色

此时上图就满足了红黑树的五个条件

条件3的代码如下

  1. /**
  2.      * 新增或者更新
  3.      * 正常增,遇到红红不平衡进行调整
  4.      * @param key
  5.      * @param value
  6.      */
  7.     public void put(int key,Object value){
  8.         Node p = this.root;
  9.         Node parent = null;//设置父节点为null
  10.         while ( p!= null){
  11.             parent = p;//将父节点跟新为当前节点
  12.             if(p.key > key){
  13.                 p = p.left;
  14.             }else if(p.key < key){
  15.                 p = p.right;
  16.             }else{
  17.                 p.value = value;   //跟新的逻辑
  18.                 return;
  19.             }
  20.         }
  21.         //创建出来的需要添加的节点
  22.         Node inserted = new Node(key, value);
  23.         //判断如果父节点为null的话,根节点就是此时需要添加的节点
  24.         if(parent == null){
  25.             root = inserted;
  26.         }
  27.         //如果key比父节点的key还小的话,父节点的左孩子就是添加的节点
  28.         else if(key < parent.key){
  29.             parent.left = inserted;
  30.             //设置此时添加节点的父节点就是上面设置好的父节点
  31.             inserted.parent = parent;
  32.         }else
  33.         //如果key比父节点的key大的话,父节点的右孩子就是添加的节点
  34.         {
  35.             parent.right = inserted;
  36.             //设置此时添加节点的父节点就是上面设置好的父节点
  37.             inserted.parent = parent;
  38.         }
  39.         //遇到红红不平衡进行调整
  40.         fixRedRed(inserted);
  41.     }
  42.  
  43.     /**
  44.      * 遇到红红不平衡的进行调整
  45.      * @param x
  46.      */
  47.     private void fixRedRed(Node x){
  48.         //1.判断如果插入节点为根节点的话,直接变黑即可
  49.         if(x == root){
  50.             x.color = Color.BLACK;
  51.             return;
  52.         }
  53.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  54.         if(isBlack(x.parent)){
  55.             return;
  56.         }
  57.         //找打父亲节点
  58.         Node parent = x.parent;
  59.         //找到叔叔节点
  60.         Node uncle = x.uncle();
  61.         //找到爷爷节点
  62.         Node grabdparent = parent.parent;
  63.         if(isRed(uncle)){
  64.             //将父节点的颜色设置为黑色
  65.             parent.color = Color.BLACK;
  66.             //将叔叔节点的颜色设置为黑色
  67.             uncle.color = Color.BLACK;
  68.             //将爷爷节点的颜色设置为红色
  69.             grabdparent.color = Color.RED;
  70.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  71.             fixRedRed(grabdparent);
  72.         }
  73.  
  74.         
  75.     }

条件4

叔叔为黑色

条件1

条件4中的条件1

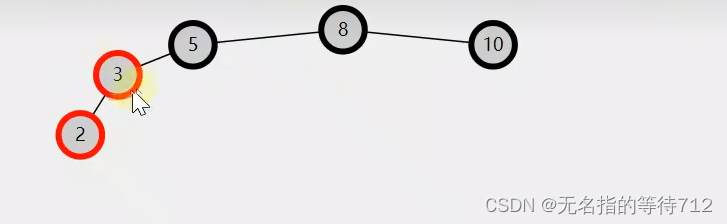
第一步:将3变为黑色,5变为红色

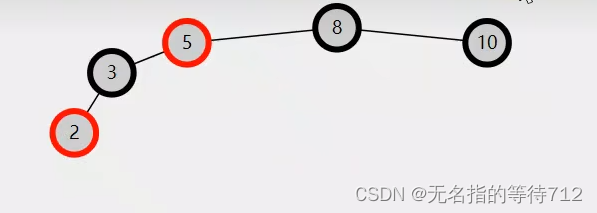
但是上图优惠让5的右孩子不满足条件5

此时3就是黄色节点,5就是粉色节点

第二步:解决办法就只能是右旋了

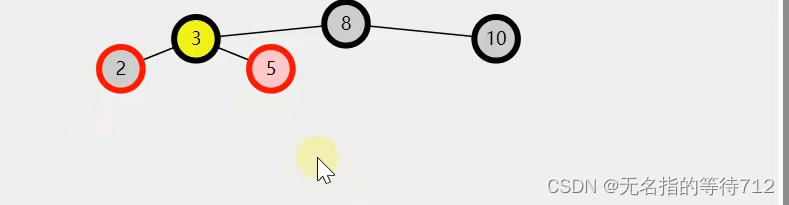
代码如下

  1. /**
  2.      * 遇到红红不平衡的进行调整
  3.      * @param x
  4.      */
  5.     private void fixRedRed(Node x){
  6.         //1.判断如果插入节点为根节点的话,直接变黑即可
  7.         if(x == root){
  8.             x.color = Color.BLACK;
  9.             return;
  10.         }
  11.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  12.         if(isBlack(x.parent)){
  13.             return;
  14.         }
  15.         //找打父亲节点
  16.         Node parent = x.parent;
  17.         //找到叔叔节点
  18.         Node uncle = x.uncle();
  19.         //找到爷爷节点
  20.         Node grabdparent = parent.parent;
  21.         if(isRed(uncle)){
  22.             //将父节点的颜色设置为黑色
  23.             parent.color = Color.BLACK;
  24.             //将叔叔节点的颜色设置为黑色
  25.             uncle.color = Color.BLACK;
  26.             //将爷爷节点的颜色设置为红色
  27.             grabdparent.color = Color.RED;
  28.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  29.             fixRedRed(grabdparent);
  30.             return;
  31.         }else{
  32.             //条件4中的条件1，如果父节点为爷爷节点的左孩子,当前传过来的节点也是左孩子的话
  33.             if(parent.isLeftChild() && x.isLeftChild()){
  34.                 //将父节点变为黑色
  35.                 parent.color = Color.BLACK;
  36.                 //将爷爷节点变为红色
  37.                 grabdparent.color = Color.RED;
  38.                 //进行右旋
  39.                 rightRotate(grabdparent);
  40.             }
  41.         }
  42.     }
条件2

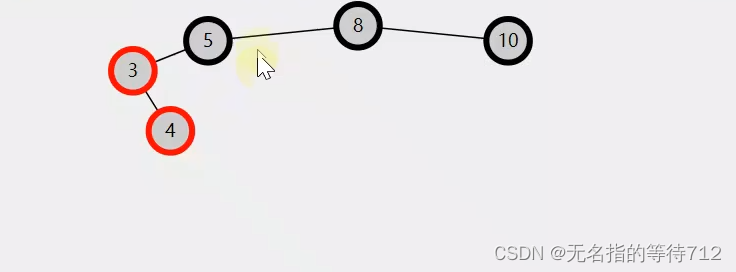
插入节点是父节点的右孩子

第一步:先进行左旋

接下来的步骤就和前面的条件1一样了

代码如下

  1.  /**
  2.      * 遇到红红不平衡的进行调整
  3.      * @param x
  4.      */
  5.     private void fixRedRed(Node x){
  6.         //1.判断如果插入节点为根节点的话,直接变黑即可
  7.         if(x == root){
  8.             x.color = Color.BLACK;
  9.             return;
  10.         }
  11.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  12.         if(isBlack(x.parent)){
  13.             return;
  14.         }
  15.         //找打父亲节点
  16.         Node parent = x.parent;
  17.         //找到叔叔节点
  18.         Node uncle = x.uncle();
  19.         //找到爷爷节点
  20.         Node grabdparent = parent.parent;
  21.         if(isRed(uncle)){
  22.             //将父节点的颜色设置为黑色
  23.             parent.color = Color.BLACK;
  24.             //将叔叔节点的颜色设置为黑色
  25.             uncle.color = Color.BLACK;
  26.             //将爷爷节点的颜色设置为红色
  27.             grabdparent.color = Color.RED;
  28.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  29.             fixRedRed(grabdparent);
  30.             return;
  31.         }else{
  32.             //条件4中的条件1，如果父节点为爷爷节点的左孩子,当前传过来的节点也是左孩子的话
  33.             if(parent.isLeftChild() && x.isLeftChild()){  //条件1
  34.                 //将父节点变为黑色
  35.                 parent.color = Color.BLACK;
  36.                 //将爷爷节点变为红色
  37.                 grabdparent.color = Color.RED;
  38.                 //进行右旋
  39.                 rightRotate(grabdparent);
  40.             }else if(parent.isLeftChild() && !x.isLeftChild()){ //条件2
  41.                 //先进行左旋
  42.                 leftRotate(parent);
  43.                 //将当前节点设置为黑色
  44.                 x.color = Color.BLACK;
  45.                 //将爷爷节点设置为红色
  46.                 grabdparent.color = Color.RED;
  47.                 //接着右旋即可
  48.                 rightRotate(grabdparent);
  49.             }
  50.         }
  51.     }
条件3
  1. /**
  2.      * 遇到红红不平衡的进行调整
  3.      * @param x
  4.      */
  5.     private void fixRedRed(Node x){
  6.         //1.判断如果插入节点为根节点的话,直接变黑即可
  7.         if(x == root){
  8.             x.color = Color.BLACK;
  9.             return;
  10.         }
  11.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  12.         if(isBlack(x.parent)){
  13.             return;
  14.         }
  15.         //找打父亲节点
  16.         Node parent = x.parent;
  17.         //找到叔叔节点
  18.         Node uncle = x.uncle();
  19.         //找到爷爷节点
  20.         Node grabdparent = parent.parent;
  21.         if(isRed(uncle)){
  22.             //将父节点的颜色设置为黑色
  23.             parent.color = Color.BLACK;
  24.             //将叔叔节点的颜色设置为黑色
  25.             uncle.color = Color.BLACK;
  26.             //将爷爷节点的颜色设置为红色
  27.             grabdparent.color = Color.RED;
  28.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  29.             fixRedRed(grabdparent);
  30.             return;
  31.         }else{
  32.             //条件4中的条件1，如果父节点为爷爷节点的左孩子,当前传过来的节点也是左孩子的话
  33.             if(parent.isLeftChild() && x.isLeftChild()){  //条件1
  34.                 //将父节点变为黑色
  35.                 parent.color = Color.BLACK;
  36.                 //将爷爷节点变为红色
  37.                 grabdparent.color = Color.RED;
  38.                 //进行右旋
  39.                 rightRotate(grabdparent);
  40.             }else if(parent.isLeftChild() && !x.isLeftChild()){ //条件2
  41.                 //先进行左旋
  42.                 leftRotate(parent);
  43.                 //将当前节点设置为黑色
  44.                 x.color = Color.BLACK;
  45.                 //将爷爷节点设置为红色
  46.                 grabdparent.color = Color.RED;
  47.                 //接着右旋即可
  48.                 rightRotate(grabdparent);
  49.             }else if(!parent.isLeftChild() && !x.isLeftChild() ){
  50.                 //将父节点变为黑色
  51.                 parent.color = Color.BLACK;
  52.                 //将爷爷节点变为红色
  53.                 grabdparent.color = Color.RED;
  54.                 //左旋
  55.                 leftRotate(grabdparent);
  56.             }
  57.        }
  58. }
条件4
  1. /**
  2.      * 遇到红红不平衡的进行调整
  3.      * @param x
  4.      */
  5.     private void fixRedRed(Node x){
  6.         //1.判断如果插入节点为根节点的话,直接变黑即可
  7.         if(x == root){
  8.             x.color = Color.BLACK;
  9.             return;
  10.         }
  11.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  12.         if(isBlack(x.parent)){
  13.             return;
  14.         }
  15.         //找打父亲节点
  16.         Node parent = x.parent;
  17.         //找到叔叔节点
  18.         Node uncle = x.uncle();
  19.         //找到爷爷节点
  20.         Node grabdparent = parent.parent;
  21.         if(isRed(uncle)){
  22.             //将父节点的颜色设置为黑色
  23.             parent.color = Color.BLACK;
  24.             //将叔叔节点的颜色设置为黑色
  25.             uncle.color = Color.BLACK;
  26.             //将爷爷节点的颜色设置为红色
  27.             grabdparent.color = Color.RED;
  28.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  29.             fixRedRed(grabdparent);
  30.             return;
  31.         }else{
  32.             //条件4中的条件1，如果父节点为爷爷节点的左孩子,当前传过来的节点也是左孩子的话
  33.             if(parent.isLeftChild() && x.isLeftChild()){  //条件1
  34.                 //将父节点变为黑色
  35.                 parent.color = Color.BLACK;
  36.                 //将爷爷节点变为红色
  37.                 grabdparent.color = Color.RED;
  38.                 //进行右旋
  39.                 rightRotate(grabdparent);
  40.             }else if(parent.isLeftChild() && !x.isLeftChild()){ //条件2
  41.                 //先进行左旋
  42.                 leftRotate(parent);
  43.                 //将当前节点设置为黑色
  44.                 x.color = Color.BLACK;
  45.                 //将爷爷节点设置为红色
  46.                 grabdparent.color = Color.RED;
  47.                 //接着右旋即可
  48.                 rightRotate(grabdparent);
  49.             }else if(!parent.isLeftChild() && !x.isLeftChild() ) {
  50.                 //将父节点变为黑色
  51.                 parent.color = Color.BLACK;
  52.                 //将爷爷节点变为红色
  53.                 grabdparent.color = Color.RED;
  54.                 //左旋
  55.                 leftRotate(grabdparent);
  56.             } else{
  57.                 //将父节点进行右旋
  58.                 rightRotate(parent);
  59.                 //将当前节点设置为黑色
  60.                 x.color = Color.BLACK;
  61.                 //将爷爷节点设置为红色
  62.                 grabdparent.color = Color.RED;
  63.                 //左旋
  64.                 leftRotate(grabdparent);
  65.             }
  66.         }
  67.     }

删除

再删除之前先写两个辅助方法

  1. //查找删除节点
  2.    private Node find(int key){
  3.         Node p = root;
  4.         while (p!=null){
  5.             if(key < p.key){
  6.                 p = p.left;
  7.             }else if(key > p.key){
  8.                 p = p.right;
  9.             }else{
  10.                 return p;
  11.             }
  12.         }
  13.         return null;
  14.     }
  15.  
  16.     //查找剩余节点
  17.    private Node findReplaced(Node deleted){
  18.         //当删除节点的左右孩子都不存在时
  19.         if(deleted.left == null && deleted.right == null){
  20.             return null;
  21.         }
  22.         //当删除节点没有左孩子,只有右孩子的话执行下面这句
  23.         if(deleted.left == null && deleted.right != null){
  24.             return deleted.right;
  25.         }
  26.         //当删除节点只有左孩子,没有右孩子的话
  27.         if(deleted.left != null && deleted.right ==null){
  28.             return deleted.left;
  29.         }
  30.         //当删除节点有两个孩子的时候需要找到后继节点
  31.         Node s = deleted.right;
  32.         //当删除节点的左孩子不等于null的时候,后继节点就一直循环,直到找到后继节点为止
  33.         while (s.left != null){
  34.             s = s.left;
  35.         }
  36.         return s;
  37.     }

执行删除任务

  1. /**
  2.      * 删除,正常删除,会用到李代桃僵的技巧,遇到嘿嘿不平衡进行调整
  3.      * @param key
  4.      */
  5.     public void remove(int key){
  6.         //查找删除的节点
  7.         Node deleted = find(key);
  8.         //如果删除节点为null的时候直接return掉,就不往下执行了
  9.         if(deleted == null){
  10.             return;
  11.         }
  12.         //进行删除操作
  13.         doRemove(deleted);
  14.     }
  15.  
  16.     private void doRemove(Node deleted) {
  17.         //查找到删除剩下的节点
  18.         Node replaced = findReplaced(deleted);
  19.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  20.             return;
  21.         }
  22.         //有一个孩子的情况
  23.         if(deleted.left == null || deleted.right == null){
  24.  
  25.             return;
  26.         }
  27.         //有两个孩子
  28.  
  29.     }

接下来就需要考虑有几个孩子的情况,来分别执行对应代码

两个孩子

其实本质上就是将删除节点和删除后剩下的节点的key值和value值进行交换

代码如下

  1. private void doRemove(Node deleted) {
  2.         //查找到删除剩下的节点
  3.         Node replaced = findReplaced(deleted);
  4.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  5.             return;
  6.         }
  7.         //有一个孩子的情况
  8.         if(deleted.left == null || deleted.right == null){
  9.  
  10.             return;
  11.         }
  12.         //有两个孩子=======>有一个孩子或没有孩子的情况了
  13.         int t = deleted.key;  //找到删除节点的key
  14.         deleted.key = replaced.key; //找到删除后留剩下的节点key,其实也就是找到后继节点,将后继节点的key变为删除节点的key
  15.         replaced.key = t;   //删除后剩下节点的key等于删除节点的key,只是也就是做一个交换,将两个节点的key
  16.  
  17.         //下面的三行代码是用来交换值的
  18.         Object v = deleted.value;
  19.         deleted.value = replaced.value;
  20.         replaced.value = v;
  21.  
  22.         //接下来删除要删除的那个节点,就可以将有两个孩子的情况转换成为只有一个孩子的情况,或者是转换成没有孩子的情况
  23.         doRemove(replaced);
  24.  
  25.     }
没有孩子根节点
  1. private void doRemove(Node deleted) {
  2.         //查找到删除剩下的节点
  3.         Node replaced = findReplaced(deleted);
  4.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  5.             if(deleted == root){
  6.                 root = null;
  7.             }
  8.             return;
  9.         }
  10.         //有一个孩子的情况
  11.         if(deleted.left == null || deleted.right == null){
  12.           
  13.             return;
  14.         }
  15.         //有两个孩子=======>有一个孩子或没有孩子的情况了
  16.         int t = deleted.key;  //找到删除节点的key
  17.         deleted.key = replaced.key; //找到删除后留剩下的节点key,其实也就是找到后继节点,将后继节点的key变为删除节点的key
  18.         replaced.key = t;   //删除后剩下节点的key等于删除节点的key,只是也就是做一个交换,将两个节点的key
  19.  
  20.         //下面的三行代码是用来交换值的
  21.         Object v = deleted.value;
  22.         deleted.value = replaced.value;
  23.         replaced.value = v;
  24.  
  25.         //接下来删除要删除的那个节点,就可以将有两个孩子的情况转换成为只有一个孩子的情况,或者是转换成没有孩子的情况
  26.         doRemove(replaced);
  27.  
  28.     }
一个孩子根节点

使用李代桃僵的方式进行替换

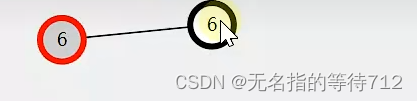
  1. private void doRemove(Node deleted) {
  2.         //查找到删除剩下的节点
  3.         Node replaced = findReplaced(deleted);
  4.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  5.             if(deleted == root){
  6.                 root = null;
  7.             }
  8.             return;
  9.         }
  10.         //有一个孩子的情况
  11.         if(deleted.left == null || deleted.right == null){
  12.             if(deleted == root){
  13.                 //用剩余节点替换了根节点的key,value，根节点孩子为null,颜色保持黑色不变
  14.                 root.key = replaced.key;
  15.                 root.value = replaced.value;
  16.                 root.left = root.right = null;
  17.             }
  18.             return;
  19.         }
  20.         //有两个孩子=======>有一个孩子或没有孩子的情况了
  21.         int t = deleted.key;  //找到删除节点的key
  22.         deleted.key = replaced.key; //找到删除后留剩下的节点key,其实也就是找到后继节点,将后继节点的key变为删除节点的key
  23.         replaced.key = t;   //删除后剩下节点的key等于删除节点的key,只是也就是做一个交换,将两个节点的key
  24.  
  25.         //下面的三行代码是用来交换值的
  26.         Object v = deleted.value;
  27.         deleted.value = replaced.value;
  28.         replaced.value = v;
  29.  
  30.         //接下来删除要删除的那个节点,就可以将有两个孩子的情况转换成为只有一个孩子的情况,或者是转换成没有孩子的情况
  31.         doRemove(replaced);
  32.  
  33.     }
没有孩子和一个孩子不在根节点的情况
  1.  private void doRemove(Node deleted) {
  2.         //查找到删除剩下的节点
  3.         Node replaced = findReplaced(deleted);
  4.         Node parent = deleted.parent;//找到被删除节点的父节点
  5.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  6.             if(deleted == root){
  7.                 root = null;
  8.             }else{
  9.                 if(isBlack(deleted)){
  10.                     //复杂调整
  11.                 }else{
  12.                     //红色叶子,无需任何处理
  13.  
  14.                 }
  15.                 //如果被删除的节点是父节点的左侧,将左侧的孩子置为null
  16.                 if(deleted.isLeftChild()){
  17.                     parent.left = null;
  18.                 }else{
  19.                     //如果被删除的节点是父节点的右侧,将右侧的孩子置为null
  20.                     parent.right = null;
  21.                 }
  22.                 //将被删除节点的父节点也置为空
  23.                 deleted.parent = null;
  24.             }
  25.             return;
  26.         }
  27.         //有一个孩子的情况
  28.         if(deleted.left == null || deleted.right == null){
  29.             if(deleted == root){
  30.                 //用剩余节点替换了根节点的key,value，根节点孩子为null,颜色保持黑色不变
  31.                 root.key = replaced.key;
  32.                 root.value = replaced.value;
  33.                 root.left = root.right = null;
  34.             }else{
  35.                 //判断如果被删除的节点不是根节点,并且被删除的节点在父节点的左侧的话,将父节点的左侧置为删除剩下的节点
  36.                 if(deleted.isLeftChild()){
  37.                     parent.left = replaced;
  38.                 }else{
  39.                     //判断如果被删除的节点不是根节点,并且被删除的节点在父节点的右侧的话,将父节点的右侧置为删除剩下的节点
  40.                     parent.right = replaced;
  41.                 }
  42.                 //被删除剩下的节点的父节点就变为了被删除节点的父节点
  43.                 replaced.parent = parent;
  44.                 //下面三行代码的意思实际上就是将被删除节点进行垃圾回收
  45.                 deleted.left = null;
  46.                 deleted.right = null;
  47.                 deleted.parent = null;
  48.  
  49.                 //当被删除的节点和剩下的节点都是黑色的时候
  50.                 if(isBlack(deleted) && isBlack(replaced)){
  51.                     //复杂处理
  52.                 }else{
  53.                     //当删除的节点是黑色,但是剩下的节点是红色的话,将剩下的这个红色节点变为黑色
  54.                     replaced.color = Color.BLACK;
  55.                 }
  56.             }
  57.             return;
  58.         }
  59.         //有两个孩子=======>有一个孩子或没有孩子的情况了
  60.         int t = deleted.key;  //找到删除节点的key
  61.         deleted.key = replaced.key; //找到删除后留剩下的节点key,其实也就是找到后继节点,将后继节点的key变为删除节点的key
  62.         replaced.key = t;   //删除后剩下节点的key等于删除节点的key,只是也就是做一个交换,将两个节点的key
  63.  
  64.         //下面的三行代码是用来交换值的
  65.         Object v = deleted.value;
  66.         deleted.value = replaced.value;
  67.         replaced.value = v;
  68.  
  69.         //接下来删除要删除的那个节点,就可以将有两个孩子的情况转换成为只有一个孩子的情况,或者是转换成没有孩子的情况
  70.         doRemove(replaced);
  71.  
  72.     }
复杂调整的函数

复杂函数又被分为了三种情况

  1. 被调整节点的兄弟为红,此时两个侄子定为黑色节点
  2. 被调整节点的兄弟为黑,两个侄子都为黑色节点
  3. 被调整节点的兄弟为黑,至少一个红色侄子
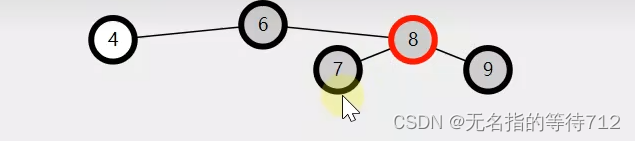
条件1

被调整节点的兄弟为红,此时两个侄子定位黑色节点

  1. //如果删除的节点和被删除的节点都是黑色节点的情况下,进行复杂调整的函数
  2.     private void fixDoubleBlack(Node x){
  3.         if(x == root){
  4.             return;
  5.         }
  6.         //找到父节点
  7.         Node parent = x.parent;
  8.         //找到兄弟节点
  9.         Node sibling = x.sibling();
  10.         //条件1
  11.         if(isRed(sibling)){
  12.             if(x.isLeftChild()){
  13.                 leftRotate(parent);
  14.             }else{
  15.                 rightRotate(parent);
  16.             }
  17.             parent.color = Color.RED;
  18.             sibling.color = Color.BLACK;
  19.             fixDoubleBlack(x);
  20.             return;
  21.         }
  22.     }
条件2条件3

被调整节点的兄弟是黑色,两个侄子也是黑色

  1. //条件2
  2.         if(sibling != null){
  3.             if(isBlack(sibling.left) && isBlack(sibling.right)){
  4.                 sibling.color = Color.RED;
  5.                 if(isRed(parent)){
  6.                     parent.color = Color.BLACK;
  7.                 }else{
  8.                     fixDoubleBlack(parent);
  9.                 }
  10.             }
  11.             //条件3兄弟是黑色,侄子是红色
  12.             else{
  13.                 if(sibling.isLeftChild() && isRed(sibling.left)){
  14.                     rightRotate(parent);
  15.                     sibling.left.color = Color.BLACK;
  16.                     sibling.color = parent.color;
  17.                 }else if(sibling.isLeftChild() && isRed(sibling.right)){
  18.                     sibling.right.color = parent.color;
  19.                     leftRotate(sibling);
  20.                     rightRotate(parent);
  21.                 }else if(!sibling.isLeftChild() && isRed(sibling.left)){
  22.                     sibling.left.color = parent.color;
  23.                     rightRotate(sibling);
  24.                     leftRotate(parent);
  25.                 }else{
  26.                     leftRotate(parent);
  27.                     sibling.right.color = Color.BLACK;
  28.                     sibling.color = parent.color;
  29.                 }
  30.                 parent.color = Color.BLACK;
  31.             }
  32.         }else{
  33.             fixDoubleBlack(parent);
  34.         }

总代码

  1. public class RedBlackTree {
  2.  
  3.     //枚举
  4.     enum Color {
  5.         RED,BLACK;
  6.     }
  7.     //根节点
  8.     private Node root;
  9.  
  10.     //红黑树节点
  11.     private static class Node {
  12.         int key;
  13.         Object value;
  14.         Node left;
  15.         Node right;
  16.         Node parent;    //父节点
  17.         Color color;
  18.  
  19.         public Node(int key, Object value) {
  20.             this.key = key;
  21.         }
  22.  
  23.         //判断当前节点是否是左孩子
  24.         boolean isLeftChild(){
  25.             //如果父节点都为null的话,根本就不可能会有左孩子,同样如果父节点的左孩子不是当前节点的话也可以判断当前节点不是左孩子
  26.             return parent != null && parent.left == this;
  27.         }
  28.  
  29.         //返回当前节点的叔叔节点
  30.         Node uncle(){
  31.             //判断如果当前节点的父节点和爷爷节点有一个为null的话,就可以判断当前节点并没有叔叔节点
  32.             if(parent == null || parent.parent == null){
  33.                 return null;
  34.             }
  35.             //判断父节点是否是爷爷节点的左孩子,如果是返回爷爷节点的右孩子
  36.             if(parent.isLeftChild()){
  37.                 return parent.parent.right;
  38.             }else{
  39.                 return parent.parent.left;
  40.             }
  41.         }
  42.  
  43.         //返回当前的兄弟节点
  44.         Node sibling(){
  45.             //判断当前节点的父节点如果为null了的话,就不会有兄弟节点了
  46.             if(parent == null){
  47.                 return null;
  48.             }
  49.             //判断如果当前节点是父节点的左孩子,则返回右节点,反之返回左节点
  50.             if(this.isLeftChild()){
  51.                 return parent.right;
  52.             }else{
  53.                 return parent.left;
  54.             }
  55.         }
  56.     }
  57.  
  58.     //判断当前节点是否是红色
  59.     boolean isRed(Node node){
  60.         //判断如果当前节点不为null，并且当前节点的颜色等于红色的时候才是红色节点
  61.         return node != null && node.color == Color.RED;
  62.     }
  63.  
  64.     //判断当前节点是否是黑色节点
  65.     boolean isBlack(Node node){
  66.         //如果不是红色节点就是黑色节点
  67.         return !isRed(node);
  68.     }
  69.  
  70.     /**
  71.      * 右旋函数
  72.      *  1.对于parent的处理
  73.      *  2.旋转后行嗯的父子关系
  74.      * @param pink
  75.      */
  76.     private void  rightRotate(Node pink){
  77.         //找到粉色节点的父节点
  78.         Node parent = pink.parent;
  79.         //pink节点的左孩子是yellow节点
  80.         Node yellow = pink.left;
  81.         //green节点是yellow节点的右侧孩子
  82.         Node green = yellow.right;
  83.         //判断当前绿色节点不为null的话,绿色节点的父节点就应该等于粉色节点
  84.         if(green != null){
  85.             green.parent = pink;
  86.         }
  87.         //旋转之后让黄色节点的右孩子等于粉色节点
  88.         yellow.right = pink;
  89.         //旋转之后黄色节点的父节点等于粉色节点的父节点
  90.         yellow.parent = pink.parent;
  91.         //旋转之后粉色节点的左孩子等于绿色节点
  92.         pink.left = green;
  93.         //旋转之后粉色节点的父节点等于黄色节点
  94.         pink.parent = yellow;
  95.         //判断如果粉色节点的父节点为null的话,根节点就变为黄色节点
  96.         if(parent == null ){
  97.             root = yellow;
  98.         }
  99.         //如果父节点的左孩子是粉色节点的话
  100.         else if(parent.left == pink){
  101.             //父节点的左孩子就等于黄色节点
  102.             parent.left = yellow;
  103.         }else{
  104.             //父节点的右孩子就等于黄色节点
  105.             parent.right = yellow;
  106.         }
  107.     }
  108.  
  109.     /**
  110.      * 左旋函数
  111.      *
  112.      * @param pink
  113.      */
  114.     private void leftRotate(Node pink) {
  115.         // 找到粉色节点的父节点
  116.         Node parent = pink.parent;
  117.         // 粉色节点的右孩子是黄色节点
  118.         Node yellow = pink.right;
  119.         // 绿色节点是黄色节点的左侧孩子
  120.         Node green = yellow.left;
  121.         // 如果绿色节点不为null，将绿色节点的父节点设为粉色节点
  122.         if (green != null) {
  123.             green.parent = pink;
  124.         }
  125.         // 旋转后，将黄色节点的左孩子设为粉色节点
  126.         yellow.left = pink;
  127.         // 将黄色节点的父节点设为粉色节点的父节点
  128.         yellow.parent = pink.parent;
  129.         // 旋转后，将粉色节点的右孩子设为绿色节点
  130.         pink.right = green;
  131.         // 将粉色节点的父节点设为黄色节点
  132.         pink.parent = yellow;
  133.         // 如果粉色节点的父节点为null，将黄色节点设为新的根节点
  134.         if (parent == null) {
  135.             root = yellow;
  136.         }
  137.         // 如果粉色节点是其父节点的左孩子，更新父节点的左孩子为黄色节点
  138.         else if (parent.left == pink) {
  139.             parent.left = yellow;
  140.         }
  141.         // 如果粉色节点是其父节点的右孩子，更新父节点的右孩子为黄色节点
  142.         else {
  143.             parent.right = yellow;
  144.         }
  145.     }
  146.  
  147.     /**
  148.      * 新增或者更新
  149.      * 正常增,遇到红红不平衡进行调整
  150.      * @param key
  151.      * @param value
  152.      */
  153.     public void put(int key,Object value){
  154.         Node p = this.root;
  155.         Node parent = null;//设置父节点为null
  156.         while ( p!= null){
  157.             parent = p;//将父节点跟新为当前节点
  158.             if(p.key > key){
  159.                 p = p.left;
  160.             }else if(p.key < key){
  161.                 p = p.right;
  162.             }else{
  163.                 p.value = value;   //跟新的逻辑
  164.                 return;
  165.             }
  166.         }
  167.         //创建出来的需要添加的节点
  168.         Node inserted = new Node(key, value);
  169.         //判断如果父节点为null的话,根节点就是此时需要添加的节点
  170.         if(parent == null){
  171.             root = inserted;
  172.         }
  173.         //如果key比父节点的key还小的话,父节点的左孩子就是添加的节点
  174.         else if(key < parent.key){
  175.             parent.left = inserted;
  176.             //设置此时添加节点的父节点就是上面设置好的父节点
  177.             inserted.parent = parent;
  178.         }else
  179.         //如果key比父节点的key大的话,父节点的右孩子就是添加的节点
  180.         {
  181.             parent.right = inserted;
  182.             //设置此时添加节点的父节点就是上面设置好的父节点
  183.             inserted.parent = parent;
  184.         }
  185.         //遇到红红不平衡进行调整
  186.         fixRedRed(inserted);
  187.     }
  188.  
  189.     /**
  190.      * 遇到红红不平衡的进行调整
  191.      * @param x
  192.      */
  193.     private void fixRedRed(Node x){
  194.         //1.判断如果插入节点为根节点的话,直接变黑即可
  195.         if(x == root){
  196.             x.color = Color.BLACK;
  197.             return;
  198.         }
  199.         //2.插入节点的父亲若为黑色,树的红黑性质不变,无需调整
  200.         if(isBlack(x.parent)){
  201.             return;
  202.         }
  203.         //找打父亲节点
  204.         Node parent = x.parent;
  205.         //找到叔叔节点
  206.         Node uncle = x.uncle();
  207.         //找到爷爷节点
  208.         Node grabdparent = parent.parent;
  209.         if(isRed(uncle)){
  210.             //将父节点的颜色设置为黑色
  211.             parent.color = Color.BLACK;
  212.             //将叔叔节点的颜色设置为黑色
  213.             uncle.color = Color.BLACK;
  214.             //将爷爷节点的颜色设置为红色
  215.             grabdparent.color = Color.RED;
  216.             //将爷爷节点传入到当前函数中,一直递归循环,直到将根节点设置为黑色
  217.             fixRedRed(grabdparent);
  218.             return;
  219.         }else{
  220.             //条件4中的条件1，如果父节点为爷爷节点的左孩子,当前传过来的节点也是左孩子的话
  221.             if(parent.isLeftChild() && x.isLeftChild()){  //条件1
  222.                 //将父节点变为黑色
  223.                 parent.color = Color.BLACK;
  224.                 //将爷爷节点变为红色
  225.                 grabdparent.color = Color.RED;
  226.                 //进行右旋
  227.                 rightRotate(grabdparent);
  228.             }else if(parent.isLeftChild() && !x.isLeftChild()){ //条件2
  229.                 //先进行左旋
  230.                 leftRotate(parent);
  231.                 //将当前节点设置为黑色
  232.                 x.color = Color.BLACK;
  233.                 //将爷爷节点设置为红色
  234.                 grabdparent.color = Color.RED;
  235.                 //接着右旋即可
  236.                 rightRotate(grabdparent);
  237.             }else if(!parent.isLeftChild() && !x.isLeftChild() ) {
  238.                 //将父节点变为黑色
  239.                 parent.color = Color.BLACK;
  240.                 //将爷爷节点变为红色
  241.                 grabdparent.color = Color.RED;
  242.                 //左旋
  243.                 leftRotate(grabdparent);
  244.             } else{
  245.                 //将父节点进行右旋
  246.                 rightRotate(parent);
  247.                 //将当前节点设置为黑色
  248.                 x.color = Color.BLACK;
  249.                 //将爷爷节点设置为红色
  250.                 grabdparent.color = Color.RED;
  251.                 //左旋
  252.                 leftRotate(grabdparent);
  253.             }
  254.         }
  255.     }
  256.  
  257.     /**
  258.      * 删除,正常删除,会用到李代桃僵的技巧,遇到嘿嘿不平衡进行调整
  259.      * @param key
  260.      */
  261.     public void remove(int key){
  262.         //查找删除的节点
  263.         Node deleted = find(key);
  264.         //如果删除节点为null的时候直接return掉,就不往下执行了
  265.         if(deleted == null){
  266.             return;
  267.         }
  268.         //进行删除操作
  269.         doRemove(deleted);
  270.     }
  271.  
  272.     //如果删除的节点和被删除的节点都是黑色节点的情况下,进行复杂调整的函数
  273.     private void fixDoubleBlack(Node x){
  274.         if(x == root){
  275.             return;
  276.         }
  277.         //找到父节点
  278.         Node parent = x.parent;
  279.         //找到兄弟节点
  280.         Node sibling = x.sibling();
  281.         //条件1
  282.         if(isRed(sibling)){
  283.             if(x.isLeftChild()){
  284.                 leftRotate(parent);
  285.             }else{
  286.                 rightRotate(parent);
  287.             }
  288.             parent.color = Color.RED;
  289.             sibling.color = Color.BLACK;
  290.             fixDoubleBlack(x);
  291.             return;
  292.         }
  293.         //条件2
  294.         if(sibling != null){
  295.             if(isBlack(sibling.left) && isBlack(sibling.right)){
  296.                 sibling.color = Color.RED;
  297.                 if(isRed(parent)){
  298.                     parent.color = Color.BLACK;
  299.                 }else{
  300.                     fixDoubleBlack(parent);
  301.                 }
  302.             }
  303.             //条件3兄弟是黑色,侄子是红色
  304.             else{
  305.                 if(sibling.isLeftChild() && isRed(sibling.left)){
  306.                     rightRotate(parent);
  307.                     sibling.left.color = Color.BLACK;
  308.                     sibling.color = parent.color;
  309.                 }else if(sibling.isLeftChild() && isRed(sibling.right)){
  310.                     sibling.right.color = parent.color;
  311.                     leftRotate(sibling);
  312.                     rightRotate(parent);
  313.                 }else if(!sibling.isLeftChild() && isRed(sibling.left)){
  314.                     sibling.left.color = parent.color;
  315.                     rightRotate(sibling);
  316.                     leftRotate(parent);
  317.                 }else{
  318.                     leftRotate(parent);
  319.                     sibling.right.color = Color.BLACK;
  320.                     sibling.color = parent.color;
  321.                 }
  322.                 parent.color = Color.BLACK;
  323.             }
  324.         }else{
  325.             fixDoubleBlack(parent);
  326.         }
  327.  
  328.     }
  329.  
  330.     private void doRemove(Node deleted) {
  331.         //查找到删除剩下的节点
  332.         Node replaced = findReplaced(deleted);
  333.         Node parent = deleted.parent;//找到被删除节点的父节点
  334.         if(replaced == null){ //如果删除后留下的剩余节点为空的话,直接return,不再继续向下执行
  335.             if(deleted == root){
  336.                 root = null;
  337.             }else{
  338.                 if(isBlack(deleted)){
  339.                     //复杂调整
  340.                     fixDoubleBlack(deleted);
  341.                 }else{
  342.                     //红色叶子,无需任何处理
  343.  
  344.                 }
  345.                 //如果被删除的节点是父节点的左侧,将左侧的孩子置为null
  346.                 if(deleted.isLeftChild()){
  347.                     parent.left = null;
  348.                 }else{
  349.                     //如果被删除的节点是父节点的右侧,将右侧的孩子置为null
  350.                     parent.right = null;
  351.                 }
  352.                 //将被删除节点的父节点也置为空
  353.                 deleted.parent = null;
  354.             }
  355.             return;
  356.         }
  357.         //有一个孩子的情况
  358.         if(deleted.left == null || deleted.right == null){
  359.             if(deleted == root){
  360.                 //用剩余节点替换了根节点的key,value，根节点孩子为null,颜色保持黑色不变
  361.                 root.key = replaced.key;
  362.                 root.value = replaced.value;
  363.                 root.left = root.right = null;
  364.             }else{
  365.                 //判断如果被删除的节点不是根节点,并且被删除的节点在父节点的左侧的话,将父节点的左侧置为删除剩下的节点
  366.                 if(deleted.isLeftChild()){
  367.                     parent.left = replaced;
  368.                 }else{
  369.                     //判断如果被删除的节点不是根节点,并且被删除的节点在父节点的右侧的话,将父节点的右侧置为删除剩下的节点
  370.                     parent.right = replaced;
  371.                 }
  372.                 //被删除剩下的节点的父节点就变为了被删除节点的父节点
  373.                 replaced.parent = parent;
  374.                 //下面三行代码的意思实际上就是将被删除节点进行垃圾回收
  375.                 deleted.left = null;
  376.                 deleted.right = null;
  377.                 deleted.parent = null;
  378.  
  379.                 //当被删除的节点和剩下的节点都是黑色的时候
  380.                 if(isBlack(deleted) && isBlack(replaced)){
  381.                     //复杂处理
  382.                     fixDoubleBlack(replaced);
  383.                 }else{
  384.                     //当删除的节点是黑色,但是剩下的节点是红色的话,将剩下的这个红色节点变为黑色
  385.                     replaced.color = Color.BLACK;
  386.                 }
  387.             }
  388.             return;
  389.         }
  390.         //有两个孩子=======>有一个孩子或没有孩子的情况了
  391.         int t = deleted.key;  //找到删除节点的key
  392.         deleted.key = replaced.key; //找到删除后留剩下的节点key,其实也就是找到后继节点,将后继节点的key变为删除节点的key
  393.         replaced.key = t;   //删除后剩下节点的key等于删除节点的key,只是也就是做一个交换,将两个节点的key
  394.  
  395.         //下面的三行代码是用来交换值的
  396.         Object v = deleted.value;
  397.         deleted.value = replaced.value;
  398.         replaced.value = v;
  399.  
  400.         //接下来删除要删除的那个节点,就可以将有两个孩子的情况转换成为只有一个孩子的情况,或者是转换成没有孩子的情况
  401.         doRemove(replaced);
  402.  
  403.     }
  404.  
  405.     //查找删除节点
  406.    private Node find(int key){
  407.         Node p = root;
  408.         while (p!=null){
  409.             if(key < p.key){
  410.                 p = p.left;
  411.             }else if(key > p.key){
  412.                 p = p.right;
  413.             }else{
  414.                 return p;
  415.             }
  416.         }
  417.         return null;
  418.     }
  419.  
  420.     //查找剩余节点
  421.    private Node findReplaced(Node deleted){
  422.         //当删除节点的左右孩子都不存在时
  423.         if(deleted.left == null && deleted.right == null){
  424.             return null;
  425.         }
  426.         //当删除节点没有左孩子,只有右孩子的话执行下面这句
  427.         if(deleted.left == null && deleted.right != null){
  428.             return deleted.right;
  429.         }
  430.         //当删除节点只有左孩子,没有右孩子的话
  431.         if(deleted.left != null && deleted.right ==null){
  432.             return deleted.left;
  433.         }
  434.         //当删除节点有两个孩子的时候需要找到后继节点
  435.         Node s = deleted.right;
  436.         //当删除节点的左孩子不等于null的时候,后继节点就一直循环,直到找到后继节点为止
  437.         while (s.left != null){
  438.             s = s.left;
  439.         }
  440.         return s;
  441.     }
  442.  
  443. }

声明：本文内容由网友自发贡献，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：【wpsshop博客】
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号