【论文阅读 | 三维重建】3D Gaussian Splatting for Real-Time Radiance Field Rendering（3DGS）_3d gaussian splatting论文

Abstract

辐射场方法最近彻底改变了用多张照片或视频捕获的新颖视图合成，然而实现高视觉质量仍然需要训练和渲染成本高昂的神经网络，而最近更快的方法不可避免地要牺牲速度来换取质量。对于无边界和完整的场景和1080P分辨率的渲染，目前没有任何方法可以实现实时显示速率。我们介绍了三个关键因素，使能够在保持有竞争力的训练时间的同时实现最先进的视觉质量。重要的是可以在1080P分辨率下实现高质量的实时（30 FPS）新视图合成。

1. 从相机校准过程中产生的稀疏点开始，用3D高斯表示场景，保留连续体积辐射场的所需属性以进行场景优化，同时避免在空白空间中进行不必要的计算；
2. 对3D高斯进行交错优化/密度控制，特别是优化各向异性协方差以实现场景的准确表示；
3. 开发了快速可见性感知渲染算法，支持各向异性泼溅，既加速训练又允许实时渲染。

我们在几个已建立的数据集上展示了最先进的视觉质量和实时渲染。

1. Introduction

网格和点是最常见的三维场景表示，因为它们是显式的并且非常适合基于GPU/CUDA的快速光栅化。相比之下，最近的神经辐射场方法NeRF建立在连续场景表示的基础上，通常使用体积光线进行优化多层感知器（MLP），以对捕获的场景进行新视图的合成。类似地，目前最有效的辐射场方法通过对存储在例如voxel、hash grids 或 points 中的值进行插值来构建连续表示。虽然这些方法的连续性质有助于优化，但是渲染所需的随机采样成本高昂，并且可能会导致噪声。

本文引入了一种结合了两者优势的新方法：我们的3D高斯表示可以优化得到最先进的视觉质量和有竞争力的训练时间，而且基于图块的splatting解决方案可以确保在多个数据集上以SOTA质量实现1080p 分辨率的实时渲染。

我们的目标是允许对多张照片拍摄的场景进行实时渲染，并以与典型真实场景的最有效的先前方法一样快的优化时间创建表示。最近的方法实现了快速训练，但是很难达到当前的 SOTA NeRF 方法（Mip-NeRF360）所获得的的视觉质量。但Mip-NeRF360 的训练时间长达48小时，快速但质量较低的辐射场方法可以根据场景实现交互式渲染时间（每秒10-15帧），但在高分辨率下无法实现实时渲染。

本文方法建立在三个主要组件之上。

1. 首先介绍3D高斯作为灵活且富有表现力的场景表示。我们从与之前类似NeRF的方法相同的输入开始，即使用运动结构（SfM）校准的相机并使用作为SfM过程一部分的生成稀疏点云初始化3D高斯集。和大多数需要多视图立体（MVS）数据的基于点的方法相比，我们仅使用SfM点作为输入实现了高质量的结果。对于 NeRF-synthetic 数据集，即使随机初始化，我们方法也能得到高质量的结果。我们表明3D高斯是一个很好的选择，因为它们是一个可微的体积表示，它们也可以通过投影到2D并应用标准的$\alpha$混合来非常有效地光栅化，使用和NeRF相同的图像生成模型。
2. 第二个组成部分是优化3D高斯的属性——3D位置、不透明度$\alpha$、各向异性协方差和球谐系数（SH），和自适应密度控制步骤交错，在优化过程中我们添加和删除3D高斯。优化过程产生了相当紧凑、非结构化的和精确的场景表示（对于所有测试场景，约使用1-5万个高斯）。
3. 第三个组成部分是实时渲染解决方案。使用了快速GPU排序算法，并受到基于tile的光栅化的启发。然而，由于我们的3D高斯表示，我们可以执行尊重可见性排序的各向异性splatting——这归功于排序和$\alpha$混合——并通过跟踪尽可能多的排序splat的遍历，实现快速和准确的后向传播。

综上，本文贡献如下：

• 引入各向异性3D高斯作为辐射场的高质量、非结构化的表示；
• 3D 高斯特性的优化方法，和自适应密度控制交错进行，为捕获的场景创建高质量的表示；
• 针对GPU的快速可微渲染方法，具有可见性感知，允许各向异性splatting和快速反向传播来实现高质量的新视图合成。

我们在先前发布的数据集上的实验结果表明，我们可以从多视图捕获中优化我们的3D高斯，并获得与之前最佳质量的隐式辐射场方法相同或更好的质量。我们还可以达到与最快方法相似的训练速度和质量，重要的是为新视图合成首次提供高质量的实时渲染。

2. 相关工作

首先简要概述传统的重建，然后讨论基于点的渲染和辐射场工作，讨论它们的相似性。辐射场是一个广阔的领域，所以我们只关注直接相关的工作。有关该领域的完全覆盖请参阅最近的综述。

2.1 传统场景重建

第一个新视图合成方法基于光场，首先密集采样，然后允许非结构化捕获。运动结构（SfM）的出现开启了一个新领域，使用一组照片可以用于合成新视图。SfM 在相机校准期间估计稀疏点云，最初用于3D空间的简单可视化，随后多视图立体（MVS）多年来产生了令人印象深刻的三维重建算法，从而发展出一些视图合成算法。所有这些方法都将输入图像重新投影和混合到新的视图相机中，并使用几何图形来指导这种重投影。这些方法在许多情况下产生了出色的结果，但当MVS生成不存在的几何形状时，通常不能完全从未构建的区域或过度重建中恢复。最近的神经渲染算法极大地减少了此类伪影，避免了在GPU上存储所有输入图像的巨大成本，在大多数方面都优于这些方法。

2.2 神经渲染和辐射场

深度学习技术在早期被用于新视图合成；CNNs用于估计混合权重，或纹理空间解决方案。基于 MVS 的几何形状的使用是这些方法中的主要缺点，此外使用CNN 进行最终的渲染通常会导致时间闪烁。

新视角合成的体积表示由Soft3D提出；随后提出了和体积ray-matching相结合的深度学习技术，基于连续可微密度场来表示几何，这种渲染方法具有较高的成本，因为查询体积需要大量的采样点。

神经辐射场（NeRFs）引入了重要性采样和位置编码来提高质量，但使用了大型MLP会对速度产生影响。NeRF 的成功导致了后续方法的爆炸式增长，来解决质量和速度问题，通常是通过引入正则化策略；目前最先进的新视图合成图像质量是 Mip-NeRF360。虽然该方法渲染质量很高，但是训练和渲染时间都非常久；我们的方法可以通过快速的训练和实时的渲染得到和其相当的质量，甚至在某些情况下超过它的质量。

最近的方法主要集中在更快的训练和/或渲染上，主要是通过利用三种设计选择：使用空间数据结构来存储神经特征，这些特征随后在体积ray-matching中进行插值，不同的编码和MLP容量。这种方法包括空间离散化的不同变体，codebooks，以及哈希表编码等，允许完全使用较小的MLP或上述神经网络。

这些方法最显著的是IstantNGP，它使用hash grid和 occupancy grid来加速计算，并使用较小的 MLP 来表示密度和外观。还有Plenoxels 使用稀疏体素网格插值连续密度场，并且能够完全不用神经网络。这二者都利用了球谐系数：前者直接表示方向效应，后者将其输入编码到颜色网络中。虽然两者都提供了出色的结果，但是这些方法仍然难以有效地表示空白空间，部分原因是场景/捕获类型。此外，通过选择用于加速的结构化网格，在很大程度上限制了图像质量，并且对于给定的光线行进步骤需要查询许多样本点来阻碍渲染速度。我们使用的非结构化、显示的GPU友好的3D高斯实现了更快的渲染速度和更好的质量，而无需神经组件。

2.3 基于点的渲染和辐射场

基于点的方法有效地渲染断开连接和非结构化的几何样本（点云）。在最简单的形式中，点样本渲染栅格化一组固定大小的非结构化点，为此它可以利用本地支持的图像API点类型或GPU上的并行软件光栅化。虽然对底层数据为真，但是点样本渲染存在孔洞，导致混叠，并且严格不连续。高质量基于点的渲染的开创性工作通过“splatting”点原语来解决这些问题，其范围大于像素，例如圆形或椭圆圆盘、椭球体或surfels。

最近人们对基于可微点的渲染技术很感兴趣。点已经用神经特征增强并使用CNN渲染，实现快速甚至实时的试图合成。但是它们仍然依赖于初始几何体的MVS，因此继承了其伪影。最显著的是在诸如无特征/增区域或薄结构之类的困难情况下过度重建或重建不足。

基于点的混合和NeRF风格的体绘制使用基本相同的图像形成模型。颜色$C$由沿光线的体绘制给出：

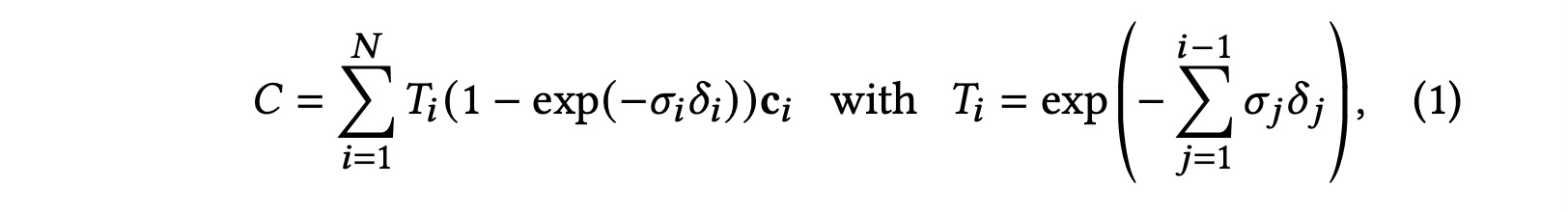
其中密度为 $\sigma$，透光率为 $T$，颜色是$c$，沿射线采样的间隔为 ${\delta }_i$。这可以写成：
$$C=\sum _{i=1}^N{T}_i{\alpha }_i{\mathbf{c}}_i$$
其中
$${\alpha }_i=\left(1-\exp \left(-{\sigma }_i{\delta }_i\right)\right)\text{ and }{T}_i=\prod _{j=1}^{i-1}\left(1-{\alpha }_i\right)\text{. }$$

典型的基于神经点的方法通过混合与像素重叠的N个有序点来计算像素的颜色C：

$$C=\sum _{i\in N}{c}_i{\alpha }_i\prod _{j=1}^{i-1}(1-{\alpha }_j),$$

其中$c_i$是每个点的颜色，并且 ${\alpha }_i$是通过评估具有协方差的2D高斯给出的并乘以学习到的不透明度。

从上面两个方程式可以看出图像形成模型一样，但是渲染算法非常不同，NeRFs是一个隐式表示空白/占用空间的连续表示，需要昂贵的随机抽样来找到方程式中的样本，随之而来的是噪声和计算开销；点是非结构化的离散表示，它足够灵活，允许创建、破坏和位移类似于NeRF的几何形状，这是通过优化不透明度和位置来实现的，同时避免完整体积表示的缺点。

Pulsar 实现了快速球体光栅化，启发了我们基于瓦片和排序的渲染器。然而，鉴于上面的分析，我们希望在排序的splat上保持近似传统的 shuffle-blending 具有体积表示的优点：我们的光栅化尊重可见性顺序。此外，我们在一个像素的所有splat上反向传播梯度并栅格化各向异性splats。这些元素都有助于结果的高视觉质量。此外，上述方法用CNN进行渲染，导致时间不稳定。尽管如此，Pulsar和ADOP的渲染速度是我们开发快速渲染解决方案的动机。

虽然专注于镜面效应，但基于漫射点渲染轨迹的神经点光线追踪方法通过使用MLP来克服这种时间不稳定性，但仍需要MVS几何作为输入。这个类别中最新的方法不需要MVS，同时也使用SH作为方向，然而只能处理单个物体的场景，并且需要mask进行初始化。虽然在小分辨率和较少点数的情况下速度较快，但是尚不清楚它如何拓展到典型数据集的场景。我们使用3D高斯函数来实现更灵活的场景表示，避免了对MVS几何的需求，并通过基于tile的渲染算法实现了对投影高斯的实时渲染。

最近的 Xu et al. 2022 方法使用点来表示辐射场，用径向基函数方法。在优化过程中采用点修剪和致密化技术，但使用体积射线行进，无法实现实时显示速率。

在人体表现捕获领域，3D高斯已经被用于表示捕获的人体。最近，它们已被用于视觉任务的体积光线行进。神经体积基元已经在类似的环境中被提出。虽然这些方法启发了3D高斯的选择作为我们的场景表示，但它们专注于重建和渲染单个孤立对象（人体或人脸）的特定情况，导致深度复杂度较小的场景。相比之下，我们对各向异性协方差的优化、交错优化/密度控制和高效深度排序进行渲染，使我们能够处理完整的、复杂的场景，包括背景，室内和室外以及深度复杂度大的场景。

3. 方法概述

我们方法的输入是静态场景的一组图像，以及由SfM校准的相应相机，SfM会产生一个稀疏点云。从这些点中，我们创建了一组3D高斯函数（第4节），由位置（均值）、协方差矩阵和不透明度