KNN算法基于实例之间的相似性进行分类或回归预测。在KNN算法中，要解决的问题是将新的数据点分配给已知类别中的某一类。该算法的核心思想是通过比较距离来确定最近邻的数据点，然后利用这些邻居的类别信息来决定待分类数据点的类别，简单来说，KNN采用测量不同特征值之间的距离方法进行分类。其核心思想为：“近朱者赤近墨者黑”。

1.2 KNN算法的一般流程

（1）收集数据

（2）准备数据：距离计算所需要的数值，最好是结构化的数据格式

（3）分析数据

（4）测试算法：计算错误率

（5）使用算法：首先需要输入样本数据和结构化的输出结果，然后运行k-近邻算法判定输入数据分别属于哪个分类，最后应用对计算出的分类执行后续的处理。

1.3 KNN算法的伪代码

对未知类别属性的数据集中的每个点依次执行以下操作：

（1）计算已知类别数据集中的点与当前点之间的距离；

（2）按照距离递增次序排序；

（3）选取与当前点距离最小的k个点；

（4）确定前k个点所在类别的出现频率；

（5）返回前k个点出现频率最高的类别作为当前点的预测分类。

二、算法实现（鸢尾花分类）

2.1数据加载和预处理

首先，代码使用`pandas`库加载了一个名为`iris.arff.csv`的数据集，并对其进行一些预处理。

`iris.arff.csv`数据集具体内容如下图所示：

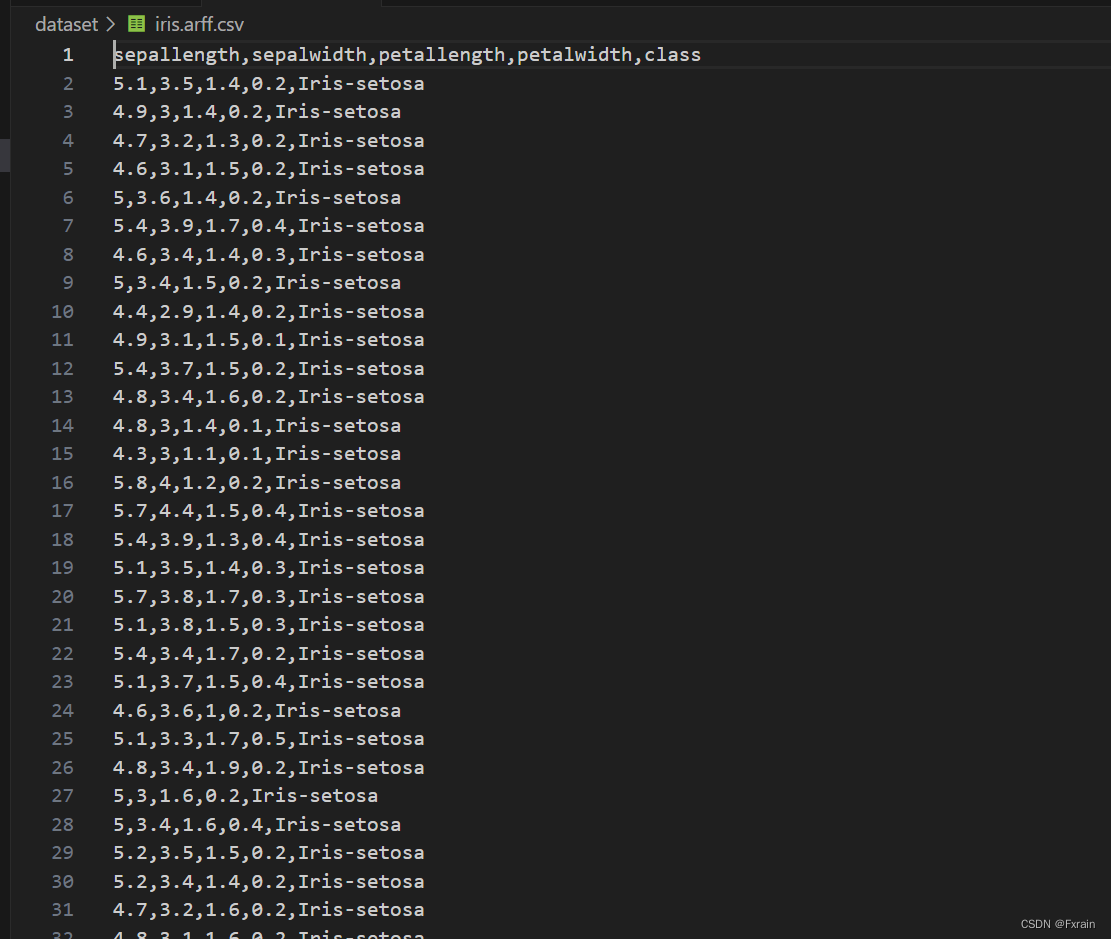
预处理包括将鸢尾花的三个类别（Iris-virginica，Iris-setosa和Iris-versicolor）映射为数字0、1和2，以便进行后续的分类。然后检查是否存在重复数据并移除，确保数据的唯一性。


#读取数据集 header参数指定标题的行 默认0
data = pd.read_csv(r'D:\ywh_knn\dataset\iris.arff.csv',header=0)
#data.head() #头5行
#data.tail() #末5行
#随机抽取15个样本 可以指定参数
data.sample(15) 
# 删除不必要的id列
#data.drop("id",axis=1,inplace=True)
data["class"] = data["class"].map({"Iris-virginica":0,"Iris-setosa":1,"Iris-versicolor":2}) # 将特征class(类别名称)映射为数字
# 观察是否有重复值
data.duplicated().any() #结果为true说明，有重复列
# 查看原始数据集记录数目
print(len(data)) #150
 
# 删除重复记录  inplace=True在原有数据集上操作
data.drop_duplicates(inplace=True)
print(len(data)) #147
# 查看各个类别的鸢尾花具有多少条记录
data["class"].value_counts()

2.2 KNN算法实现

定义了一个名为`KNN`的类，用于实现K最近邻算法。在初始化函数`__init__`中，指定了K值。KNN算法的核心部分包括`fit`和`predict`方法。`fit`方法用于训练模型，接收训练数据集X和对应的标签y，并将其转换为 NumPy 数组，并保存在self.X和self.y中。。`predict`方法用于对新样本进行预测，接收测试数据集X，并返回预测结果。

2.2.1 计算样本间的距离

在predict方法中，对于每个测试样本x，首先计算它与所有样本之间的距离，这里通过numpy，将测试样本x与所有训练样本self.X逐元素相减，然后对差值的平方求和，再对和值开方，得到了每个测试样本与所有训练样本之间的欧式距离。

用欧式距离计算两个向量点xA和xB之间的距离公式：

$d = \sqrt{(xA_{0}-xB_{0})^{2}+(xA_{1}-xB_{1})^{2}}$

接下来，对这些距离进行排序，并取前k个距离对应的索引，即找出与当前测试样本距离最近的k个训练样本。使用argsort方法对距离数组dis进行排序，返回的是排序后的索引数组，然后取前k个索引，即找到了最近的k个训练样本的索引。

最后，使用这k个训练样本的标签进行投票，选择出现次数最多的标签作为当前测试样本的预测标签。这里使用了NumPy的bincount函数，统计索引数组self.y[index]中每个元素出现的次数，然后取出现次数最多的元素，即为当前测试样本的预测标签。

2.2.2 关于Self@KNN

在机器学习中，Self@KNN是一种基于K最近邻算法的自监督学习方法。K最近邻算法是一种常用的分类和回归算法，它通过计算样本之间的距离来确定新样本的类别或数值。Self@KNN是对K最近邻算法的改进，它通过将待分类的样本与自身的K个最近邻样本进行比较，来进行分类或回归任务。

Self@KNN的核心思想是利用样本自身的信息来进行学习，而不依赖于外部标签信息。具体而言，Self@KNN首先使用无监督学习方法对样本进行特征提取，然后利用K最近邻算法对提取的特征进行分类或回归。这种方法可以在没有标签信息的情况下进行学习，从而扩展了机器学习的应用场景。


class KNN:
    def __init__(self,k):
        #初始化 k:int  邻居的个数
        self.k = k
        
    def fit(self,X,y):
        #训练方法 X:类数组类型，形状为：[样本数量，特征数量] 待训练的样本特征（属性） y: 类数组类型，形状为：[样本数量] 每个样本的目标值（标签）。
        #将X转换成ndarray数组类型。
        self.X = np.asarray(X)
        self.y = np.asarray(y)
        
    def predict(self,X):
        #根据参数传递的样本，对样本数据进行预测
        #X:类数组类型，形状为：[样本数量，特征数量] 待训练的样本特征（属性）
        #  Return result: 数组类型 预测的结果
        X = np.asarray(X)
        result = []
        # 对ndarray数组进行遍历，每次取数组一行（一个样本）。
        # x:当前测试集中的样本  self.X 训练集中的样本
        for x in X:
            # 对于测试集中的每一个样本依次与训练集中所有样本求距离
            dis = np.sqrt(np.sum((x - self.X) **2,axis=1))
            # 返回数组排序后，每个元素在原数组（排序之前的数组）中的索引
            index = dis.argsort()
            # 进行截断，只取前k个元素，【取距离最近k个元素的索引】
            index = index[:self.k]
            # 使用np.bincount()函数计算y[index]中每个元素的出现次数，元素必须是非负整数
            count = np.bincount(self.y[index])
            # 返回ndarray数组中，值最大的元素(出现次数最多的元素)对应的索引，该索引就是我们判别的类别
            result.append(count.argmax())
        return np.asarray(result)

2.3样本划分

将数据集根据类别划分为三个子集 t0, t1, t2 ，分别对应三种不同的鸢尾花类别。然后，从每个子集中随机选择40个样本作为训练集，剩余的样本作为测试集。


# 提取出每个类别鸢尾花的数据
t0 = data[data["class"] == 0] #49
t1 = data[data["class"] == 1] #48
t2 = data[data["class"] == 2] #50
#对每个类别数据进行洗牌。
t0 = t0.sample(len(t0),random_state=0)
t1 = t1.sample(len(t1),random_state=0)
t2 = t2.sample(len(t2),random_state=0)
#构建训练集与测试集
train_X = pd.concat([t0.iloc[:40,:-1],t1.iloc[:40,:-1],t2.iloc[:40,:-1]],axis=0)
train_y = pd.concat([t0.iloc[:40,-1],t1.iloc[:40,-1],t2.iloc[:40,-1]],axis=0)
test_X = pd.concat([t0.iloc[40:,:-1],t1.iloc[40:,:-1],t2.iloc[40:,:-1]],axis=0)
test_y = pd.concat([t0.iloc[40:,-1],t1.iloc[40:,-1],t2.iloc[40:,-1]],axis=0)

2.4训练与测试模型

创建一个 KNN 分类器对象 knn，传入参数 k=3。

使用训练集调用 knn.fit 方法进行训练。


# 创建KNN对象，进行训练与测试
knn = KNN(k=3)
# 进行训练
knn.fit(train_X,train_y)
# 进行测试 获得测试结果
result = knn.predict(test_X)

2.5性能评估

调用 knn.predict 方法对测试集 test_X 进行预测，得到预测结果 result。

计算预测结果与真实标签 test_y 相等的数量，并打印出来。

计算预测准确率（正确预测的数量除以总样本数量），并打印出来。


displayhook("测试结果：")
displayhook(result)        
displayhook("真实结果：")         
displayhook(test_y)
displayhook("测试样本数：")   
displayhook(np.sum(result == test_y))
displayhook("准确率：")   
displayhook(np.sum(result == test_y) / len(result))

2.6 结果可视化

使用`matplotlib`库将结果可视化。首先绘制了训练集中各个类别的样本散点图，其中不同颜色代表不同的鸢尾花品种，分别用红色、绿色、蓝色表示。然后，将测试集中被正确预测的样本用特定标记标出（用"right"表示），将被错误预测的样本用不同标记标出（用"wrong"表示）分别用青色 “x” 和紫色 “>” 表示。。


mpl.rcParams["font.family"] = "simHei"
mpl.rcParams["axes.unicode_minus"] = False
 
# {"Iris-virginica":0,"Iris-setosa":1,"Iris-versicolor":2}
#设置画布大小
plt.figure(figsize=(10,8))
# 绘制训练集数据
plt.scatter(x=t0["sepallength"][:40],y=t0["petallength"][:40],color="r",label="Iris-virginica")
plt.scatter(x=t1["sepallength"][:40],y=t1["petallength"][:40],color="g",label="Iris-setosa")
plt.scatter(x=t2["sepallength"][:40],y=t2["petallength"][:40],color="b",label="Iris-versicolor")
# 绘制测试集数据
right = test_X[result == test_y] #预测正确的
wrong = test_X[result != test_y] #预测错误的
plt.scatter(x=right["sepallength"],y=right["petallength"],color="c",marker="x",label="right")
plt.scatter(x=wrong["sepallength"],y=wrong["petallength"],color="m",marker=">",label="wrong")
plt.xlabel("花萼长度")
plt.ylabel("花瓣长度")
plt.title("KNN分类结果显示")
plt.legend(loc="best")
plt.show()

2.7 整体代码展示


from sys import displayhook
import numpy as np
import pandas as pd 
import matplotlib as mpl
import matplotlib.pyplot as plt
 
# 鸢尾花数据集
#读取数据集 header参数指定标题的行 默认0
data = pd.read_csv(r'D:\ywh_knn\dataset\iris.arff.csv',header=0)
#data.head() #头5行
#data.tail() #末5行
#随机抽取15个样本 可以指定参数
data.sample(15) 
# 删除不必要的id列
#data.drop("id",axis=1,inplace=True)
data["class"] = data["class"].map({"Iris-virginica":0,"Iris-setosa":1,"Iris-versicolor":2}) # 将特征class(类别名称)映射为数字
# 观察是否有重复值
data.duplicated().any() #结果为true说明，有重复列
# 查看原始数据集记录数目
print("原始数据集个数：")
print(len(data)) #150
 
# 删除重复记录  inplace=True在原有数据集上操作
data.drop_duplicates(inplace=True)
print("删除重复数据后的个数：")
print(len(data)) #147
# 查看各个类别的鸢尾花具有多少条记录
data["class"].value_counts()
 
class KNN:
    def __init__(self,k):
        #将传入的最近邻居数量 k 赋值给类属性 self.k，以供后续使用。
        self.k = k
        
    def fit(self,X,y):
        #X形状为：[样本数量，特征数量] 待训练的样本特征（属性）  y形状为：[样本数量] 每个样本的目标值（标签）。
        self.X = np.asarray(X)#将输入的训练数据 X 转换为 NumPy 数组，并赋值给类属性 self.X，以备后续预测使用。
        self.y = np.asarray(y)#将输入的标签数据 y 转换为 NumPy 数组，并赋值给类属性 self.y，以备后续预测使用。
        
    def predict(self,X):
        #根据参数传递的样本，对样本数据进行预测
        #X形状为：[样本数量，特征数量] 待训练的样本特征（属性）
        X = np.asarray(X)
        result = []#用于存储预测结果
        # 对数组进行遍历，每次取数组一行（一个样本）。
        # x:当前测试集中的样本  self.X 训练集中的样本
        for x in X:
            # 对于测试集中的每一个样本依次与训练集中所有样本求距离,并存储在数组 dis 中。
            dis = np.sqrt(np.sum((x - self.X) **2,axis=1))
            # 数组排序，返回每个元素在原数组（排序之前的数组）中的索引
            index = dis.argsort()
            # 进行截取，只取前k个元素，【取距离最近k个元素的索引】
            index = index[:self.k]
            # 使用np.bincount()函数计算y[index]中每个元素的出现次数
            count = np.bincount(self.y[index])
            # 返回ndarray数组中，值最大的元素(出现次数最多的元素)对应的索引，该索引就是我们判别的类别
            result.append(count.argmax())
        return np.asarray(result)
        
# 提取出每个类别鸢尾花的数据
t0 = data[data["class"] == 0] #49
t1 = data[data["class"] == 1] #48
t2 = data[data["class"] == 2] #50
#对每个类别数据进行洗牌。
t0 = t0.sample(len(t0),random_state=0)
t1 = t1.sample(len(t1),random_state=0)
t2 = t2.sample(len(t2),random_state=0)
#构建训练集与测试集
train_X = pd.concat([t0.iloc[:40,:-1],t1.iloc[:40,:-1],t2.iloc[:40,:-1]],axis=0)
train_y = pd.concat([t0.iloc[:40,-1],t1.iloc[:40,-1],t2.iloc[:40,-1]],axis=0)
test_X = pd.concat([t0.iloc[40:,:-1],t1.iloc[40:,:-1],t2.iloc[40:,:-1]],axis=0)
test_y = pd.concat([t0.iloc[40:,-1],t1.iloc[40:,-1],t2.iloc[40:,-1]],axis=0)
 
# 创建KNN对象，进行训练与测试
knn = KNN(k=3)
# 进行训练
knn.fit(train_X,train_y)
# 进行测试 获得测试结果
result = knn.predict(test_X)
displayhook("测试结果：")
displayhook(result)        
displayhook("真实结果：")         
displayhook(test_y)
displayhook("测试样本数：")   
displayhook(np.sum(result == test_y))
displayhook("准确率：")   
displayhook(np.sum(result == test_y) / len(result))
 
#设置字体为字体，以支持中文显示
mpl.rcParams["font.family"] = "simHei"
#设置在中文字体时，能正常显示负号（-）
mpl.rcParams["axes.unicode_minus"] = False
 
# {"Iris-virginica":0,"Iris-setosa":1,"Iris-versicolor":2}
#设置画布大小
plt.figure(figsize=(10,8))
# 绘制训练集数据
plt.scatter(x=t0["sepallength"][:40],y=t0["petallength"][:40],color="r",label="Iris-virginica")
plt.scatter(x=t1["sepallength"][:40],y=t1["petallength"][:40],color="g",label="Iris-setosa")
plt.scatter(x=t2["sepallength"][:40],y=t2["petallength"][:40],color="b",label="Iris-versicolor")
# 绘制测试集数据
right = test_X[result == test_y] #预测正确的
wrong = test_X[result != test_y] #预测错误的
plt.scatter(x=right["sepallength"],y=right["petallength"],color="c",marker="x",label="right")
plt.scatter(x=wrong["sepallength"],y=wrong["petallength"],color="m",marker=">",label="wrong")
plt.xlabel("花萼长度")
plt.ylabel("花瓣长度")
plt.title("KNN分类结果显示")
plt.legend(loc="best")#添加图例 自动选择最佳位置
plt.show()

三、实验结果分析

3.1实验中出现的问题

matplotlib绘制图像不支持中文（如下图所示），需要进行设置中文字体

3.2实验结果显示

终端显示：

实验结果可视化：

3.3实验总结

本次实验通过鸢尾花分类学习了KNN算法，选择样本数据集中前k个最相似的数据，就是KNN算法中k的出处。k值过大，会出现分类结果模糊的情况；k值较小，那么预测的标签比较容易受到样本的影响。在实验过程中，不同的k值也会导致分类器的错误率不同。KNN算法精度高、无数据输入的假定，可以免去训练过程。但是对于数据量较多的训练样本，KNN必须保存全部数据集，可能会存在计算的时间复杂度、空间复杂度高的情况，存在维数灾难问题。

3.4参考书籍

《机器学习实战》

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/Gausst松鼠会/article/detail/722091