K-近邻算法(KNN)_k近邻算法

1.定义:   

     k-近邻（KNN,k-NearestNeighbor）算法是一种基本分类与回归方法，我们这里只讨论分类问题中的 k-近邻算法。k-近邻算法的输入为实例的特征向量，对应于特征空间的点；输出为实例的类别，可以取多类。k-邻算法假设给定一个训练数据集，其中的实例类别已定。分类时，对新的实例，根据其 k 个最近邻的训练实例的类别，通过多数表决等方式进行预测。因此，k近邻算法不具有显式的学习过程即属于有监督学习范畴。k近邻算法实际上利用训练数据集对特征向量空间进行划分，并作为其分类的“模型”。k值的选择、距离度量以及分类决策规则是k近邻算法的三个基本要素。
    来源:KNN算法最早由Cover 和 Hart提出的一种分类算法
先看样例,根据表格，猜测未知电影的类型:  

咋一看，前三个爱情片，后三个动作片，按照常理接下来应该是继续是动作片，近邻嘛....
emmmmm,虾糕。
下面是经过KNN算法之后的结果，近邻，值最小，结论，爱情片。

          

当然了，其实仔细观察的话，看打斗镜头和接吻镜头，也是可以得出结论的喽。

2. 距离公式：

   (两点之间距离公式将坐标变为特征值)
    两个样本的距离可以通过下列公式计算，
    比如a(x1,y1,z1),b(x2,y2,z2)
        (（x1-x2）^2 + (y1-y2)^2+(z1-z2)^2)^(1/2)
    又叫欧氏距离

3 KNN需要做标准化:

    不做标准化处理，可能会造成某个特征值对结果的影响过大

4.k-近邻算法API

   sklearn.neighbors.KNeighborsClassifier(n_negihbors=5,algorithm="auto")
        n_neighbors:int 可选(默认5)，k_neighbors查询默认使用的邻居数
        algorithm:{"auto","ball_tree","kd_tree","brute"}计算邻居的算法
                  ball_tree将使用BallTree,kd_tree将使用KDTree,auto将尝试传递fit的值自选算法

5.k-近邻算法实例: 预测签入地点   

    数据集:https://www.kaggle.com/c/facebook-v-predicting-check-ins/data

档案说明

• train.csv，test.csv 

  • row_id：签到事件的ID

  • xy：坐标

  • 精度：位置精度 

  • 时间：时间戳

  • place_id：商家的ID，这是您要预测的目标

• sample_submission.csv-带有随机预测的正确格式的样本提交文件

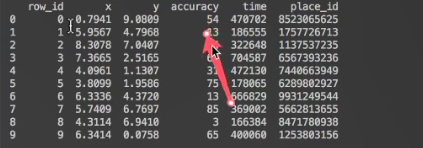
 数据集很大，大小为1.18G,这里我们稍微看下前10行，对数据有个大概的了解，也是对数据的读取:

5.1 数据的读取

data = pd.read_csv(r"./files/FBlocation/train.csv")
print(data.head())

                                     

5.2 处理数据

 
    data.query("x > 1.0 & y < 1.25 & y > 2.5 & y < 2.75")
 
 
    time_value = pd.to_datetime(data["time"],unit="s") #秒
    print(time_value)
 
    time_value =  pd.DataFrame(time_value) #年月日时分秒等变为{"year":2019,"month":01} 这样的字典格式数据
 
 
    data["day"] = time_value.day
    data["hour"] = time_value.hour
    data["weekday"] = time_value.weekday
    #删除一些特征
    data = data.drop(["time"],axis=1) 
 
    place_count = data.groupby("place_id").count() #根据place_id分组，统计次数
    tf = place_count[place_count.row_id > 3].reset_index() 
    data = data[data["place_id"].isin(tf.place_id)] #如果place_id > 3的数据保存，小于则去掉
 
 
    y = data["place_id"]
    x = data.drop(["place_id"],axis=0.25)
 
    x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.25)

                                                    

                   

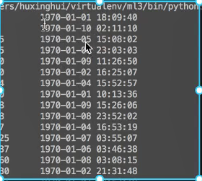
如图，将时间戳转换为标准时间后，我们发现时间基本都是在1970年的1月份，所以我们原来的时间特征改为day,hour,weekday这些有区分度的特征

5.3 我们先不对数进行标准化，直接进行算法

5.4 算法预测

    knn = KNeighborsClassifier(n_neighbors=5)
    #fit，predict,score
    knn.fit(x_train,y_train)
    #得出预测结果
    y_predict= knn.predict(x_test)
    print("预测的目标签入位置为",y_predict)
    #得出正确率
    correctRate = knn.score(x_test,y_test)
    print(correctRate) 

 签入位置和预测正确率:

                              

可以看到，正确率为2.7%, 预测效果极差。

5.5 标准化后再进行算法预测

  
    std = StandardScaler()
 
    x_train_std = std.fit_transform(x_train)
    # y_train_std = std.fit_transform(y_train)#已经fit转换过了，可以直接transform()
    y_train_std = std.transform(y_train)
 
    knn = KNeighborsClassifier(n_neighbors=5)
    #fit，predict,score
    knn.fit(x_train_std,y_train_std)
 
    y_predict= knn.predict(x_test)
    print("预测的目标签入位置为",y_predict)
    #得出正确率
    correctRate = knn.score(x_test,y_test)
    print(correctRate) #

 签入位置和预测正确率:

正确率达到 40.5% 

算法优化：

      再去掉一些无关特征值，以及k值的选取(即调参)。(待优化)

6 k-近邻算法优缺点

    优点:
        简单，易于理解，易于实现，无需估计参数，无需训练
    缺点:
        .懒惰算法，对测试样本分类时的计算量大，内存开销大
        .必须指定K值，K值选择不当则分类进度不能保证
    使用场景:
        小数据场景，几千~几万样本，具体场景,具体分析