数字IC设计 FPGA——再谈乘法器设计（使用Verilog 原语 LUT 进行四位乘法器设计）_verilog lut mapping

数字IC设计 FPGA——再谈乘法器设计（使用Verilog 原语 LUT 进行四位乘法器设计）

乘法器同加法器一样，在数字信号的各种算法中被频繁的使用，并且对于整个系统的速度的影响是很大的。那么如何实现快速高效的乘法器关系着整个系统的运算速度和资源效率最大化的利用。

乘法操作分为有符号操作和无符号操作两大类，无符号操作相对于有符号乘法操作相对简单，但也只需要简单的变换就能有符号乘法器变换为无符号乘法器。

本次主要是基于Verilog 原语LUT 进行乘法器的设计。
相关的乘法器知识可以参考之前的博文：

数字电路基础知识——组合逻辑电路之乘法器的设计（一）—— 并行、移位相加、加法树、查找表乘法器
数字电路基础知识——乘法器的设计（二）（ 串行、流水线、有符号数八位乘法器）

一、乘法器架构

1. 乘法器
   由于乘数和被乘数都是二进制，所以利用人工计算来分析，所以利用乘数从最后一位到第第一位每一位依次与被乘数相乘，从第二位开始每一位都要依次左移一位，形成一个阵列的式。而由于两个一位二进制数相乘，实际上是做与运算，所以就将乘法操作简化为了与运算、移位操作以及加法操作。比如 1011与 1101相 乘，如图，实际上可看作 1011+00000+101100+1011000四个数相加。
   
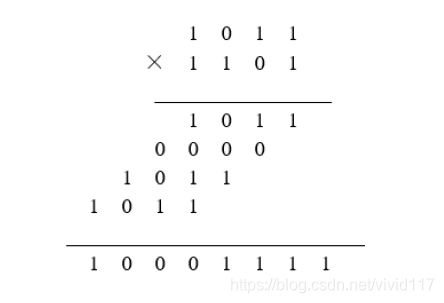
2. 乘法器结构
   乘法运算是由与、或、非等基本逻辑组合而成的，如下图所示是乘法器内部结构图
   

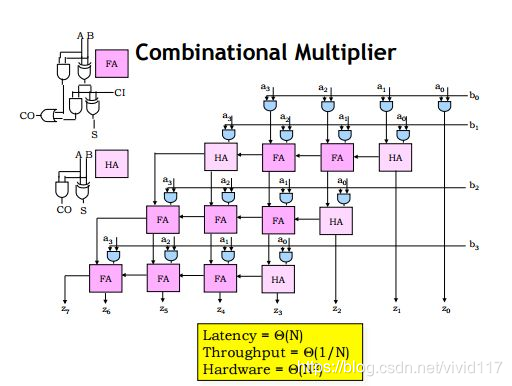
二、乘法器的 Verilog 原语设计

1. 设计思路
   使乘法器的输入分别为A[3:0]和B[3:0]，设计思路先计算出相与的结果，将相与的结果一次移位相加得到最后的结果。移位相加所使用的全加器是之前在下面这篇博客中以LUT3设计的一位全加器。
   数字IC设计 FPGA——再谈加法器设计（使用Verilog 原语 进行四位加法器设计）
   并设置中间变量：
   t0，t1，t2，t3：第一行至第四行相与的结果
   ts0，ts1，ts2，ts3：第一行至第四行的结果输出
   tc0，tc1，tc2，tc3：第一行至第四行的进位输出
2. Verilog代码

module addr_4bit(
A,B,Y
    );

input [3:0] A,B;
output [7:0] Y;

wire [3:0] t0,t1,t2,t3; //每一行相与结果
wire [3:0] ts0,ts1,ts2,ts3; //每一行的相加的结果输出
wire [3:0] tc0,tc1,tc2,tc3; //每一行的进位输出

genvar i;
generate
   for (i=0;i<4;i=i+1)
   begin: label1  
        assign t0[i] = A[i] & B[0];
        assign t1[i] = A[i] & B[1];
        assign t2[i] = A[i] & B[2];
        assign t3[i] = A[i] & B[3];
   end  
endgenerate

genvar j;
generate
    for (j=0;j<4;j=j+1)
    begin:label2
        assign ts0[j]= t0[j];
        assign tc0[j] = 1'b0;
    end
endgenerate

genvar m;
generate
   for (m=0;m<3;m=m+1)
   begin: label3
        addr_bit u1(
        .A(t1[m]),
        .B(ts0[m+1]),
        .S(ts1[m]),
        .Cout(tc1[m]),
        .Cin(tc0[m])
        ); 
   end  

   for (m=0;m<3;m=m+1)
   begin: label4
        addr_bit u2(
        .A(t2[m]),
        .B(ts1[m+1]),
        .S(ts2[m]),
        .Cout(tc2[m]),
        .Cin(tc1[m])
        ); 
   end  

   for (m=0;m<3;m=m+1)
   begin: label5
        addr_bit u3(
        .A(t3[m]),
        .B(ts2[m+1]),
        .S(ts3[m]),
        .Cout(tc3[m]),
        .Cin(tc2[m])
        ); 
   end  
endgenerate


assign ts1[3]=t1[3];
assign ts2[3]=t2[3];
assign ts3[3]=t3[3];

wire [3:0] rac,ras;

assign rac[0]= 1'b0;

genvar n;
generate
    for (n=0;n<3;n=n+1)
    begin :label6
        addr_bit u4(
        .A(rac[n]),
        .B(ts3[n+1]),
        .S(ras[n]),
        .Cin(tc3[n]),
        .Cout(rac[n+1])
        );
    end
endgenerate

assign Y[0]=ts0[0];
assign Y[1]=ts1[0];
assign Y[2]=ts2[0];
assign Y[3]=ts3[0];


genvar p;
generate
    for (p=4;p<7;p=p+1)
    begin:label7
        assign Y[p]=ras[p-4];
    end
endgenerate

assign Y[7]=rac[3];
endmodule
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106

rac和ras是高四位的进位输出和结果输出相与的结果。必须要想加才能得到正确的结果。

3. RTL结构图
   
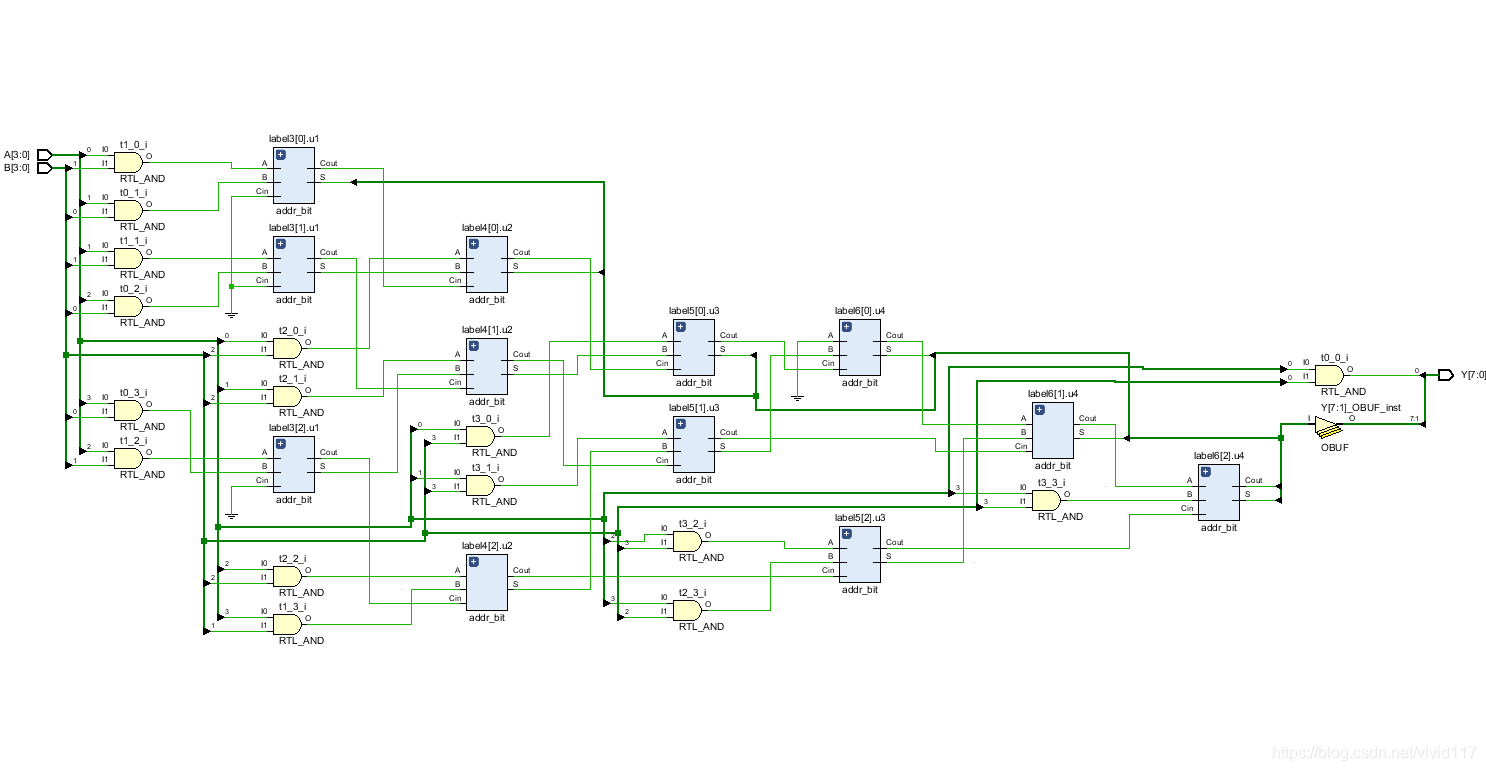
4. 仿真结果如下：
   可以看到有正确的输出结果和进位输出
   
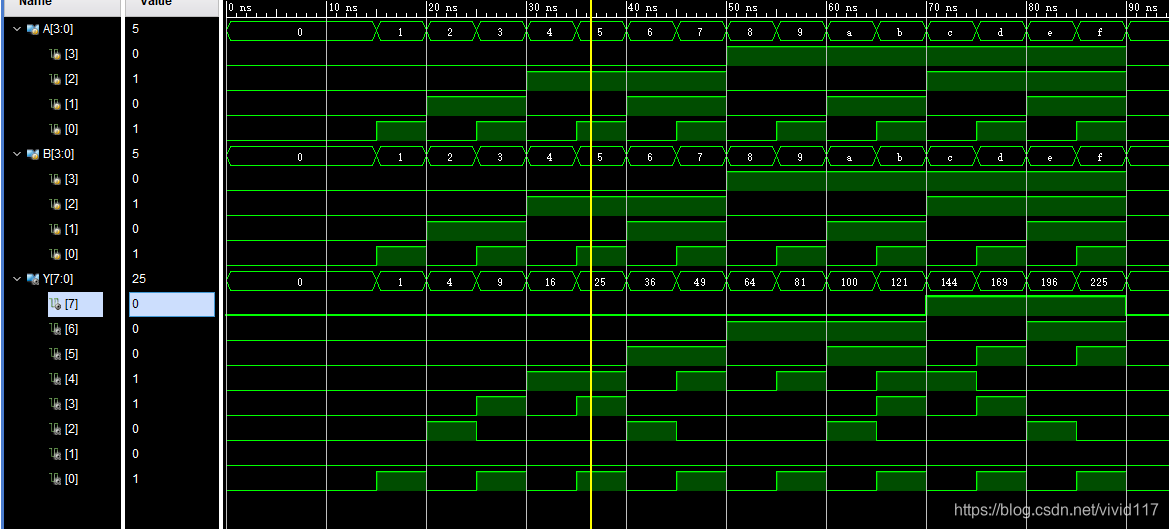
5. 综合之后资源的利用
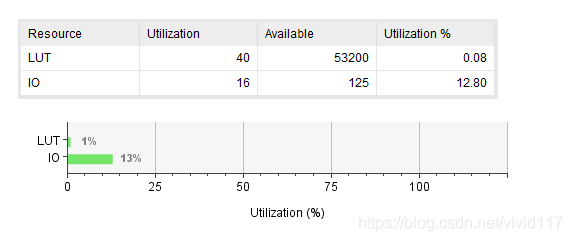
   40LUT包括24个LUT3和16个LUT2(与门)

三、总结

1. 使用该乘法器能够拓展为其他新的位宽的乘法器。该乘法器可能不是最好的乘法器架构。
2. 如果再不采用原语进行设计的情况下，直接编写加法器Verilog代码，综合工具会根据自己的算法给出一个比较合理的电路，可能会比我们采用后一种方法设计的要更好，这需要依赖EDA综合工具。
3. 但是通过了解CLB的不同的基本配置方式以及内部资源分布，对于更好理解软件综合过程和设计具有更好的指导意义
4. 如果能再关键的位置手动配置硬件资源，可能会改善局部性能，这对于高性能计算硬件有重要意义，尤其是底层的硬件加法等部件。