devbox
Cpp五条
这个屌丝很懒，什么也没留下！
关注作者
热门标签
热门文章
当前位置:   article > 正文

K近邻（K-Nearest Neighbors，简称KNN）算法_knn计算距离的方法

作者：Cpp五条 | 2024-06-11 11:49:07

赞

踩

knn计算距离的方法

K近邻（K-Nearest Neighbors，简称KNN）算法是一种常用的分类和回归算法

  • knn算法原理

当预测一个新的值x的时候，根据它距离最近的K个点是什么类别来判断x属于哪个类别。

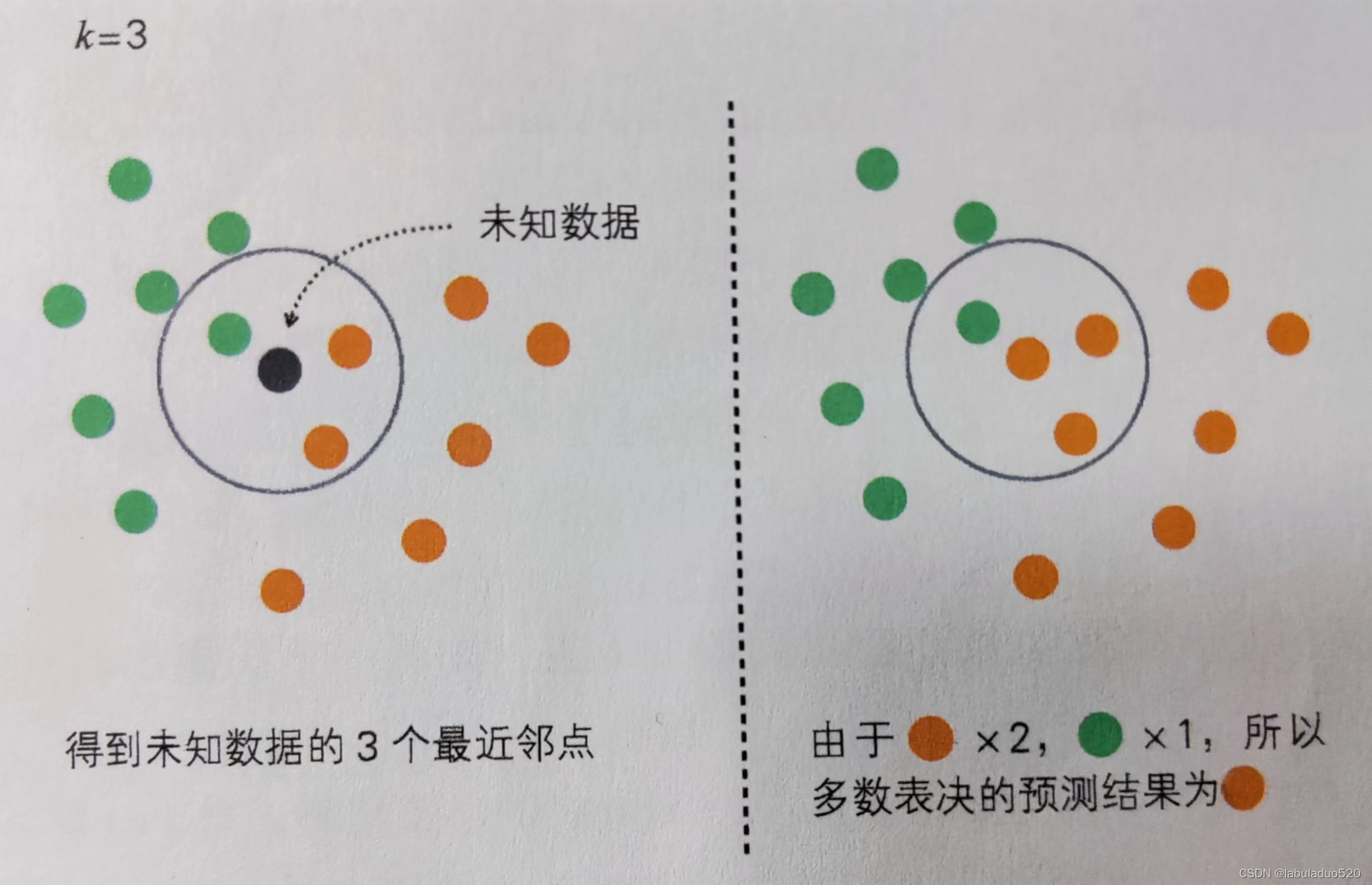
 注：通过多数表决进行分类

  • 距离计算

    要度量空间中点与点之间的距离，有好几种度量方式，比如常见的曼哈顿距离计算，欧式距离计算等。不过通常KNN算法中使用的是欧式距离。

    以二维平面为例：

     1、曼哈顿距离：

d=\left | x2-x1 \right |+\left | y2-y1 \right |

     2、欧氏距离：

欧氏距离其实就是我们高中时所学的两点之间距离的计算公式

d=\sqrt{(x2-x1)^{2}+(y2-y1)^{2}}

  • 代码实现

     1、基于sklearn中的鸢尾花数据集手写knn算法

  1. import numpy as np
  2. from sklearn.datasets import load_iris
  3. from sklearn.model_selection import train_test_split
  4. from sklearn.metrics import accuracy_score
  5.  
  6. # 定义KNN算法类
  7. class KNN:
  8.     # KNN算法初始化
  9.     def __init__(self, n_neighbors=5):
  10.         self.n_neighbors = n_neighbors
  11.  
  12.     def fit(self, X, y):
  13.         self.X = X
  14.         self.y = y
  15.                                         
  16.     def euclidean_distance(self, x1, x2): 
  17.         return np.sqrt(np.sum((x1 - x2) ** 2)) # 两个向量
  18.  
  19.     def predict(self, X_test):  
  20.         y_pred = []
  21.         for test_sample in X_test:
  22.             distances = [self.euclidean_distance(test_sample, x) for x in self.X]
  23.             nearest_indices:numpy.ndarray = np.argsort(distances)[:self.n_neighbors] # 排序
  24.             nearest_labels = self.y[nearest_indices]
  25.             unique_labels, counts = np.unique(nearest_labels, return_counts=True)# 返回值是一个包含两个数组的元组，第一个数组是唯一的标签值，第二个数组是对应每个唯一标签值的计数
  26.             predicted_label = unique_labels[np.argmax(counts)] # np.argmax(counts)返回数组中最大元素的索引
  27.             y_pred.append(predicted_label)
  28.         return np.array(y_pred) # 将预测结果转换为数组并返回  
  29.  
  30. # 加载鸢尾花数据集
  31. iris = load_iris()
  32. x = iris.data
  33. y = iris.target
  34.  
  35. # 划分训练集和测试集
  36. x_train, x_test, y_train, y_test = train_test_split(x, y, test_size=0.3, random_state=100)
  37.  
  38. # 实例化KNN算法类
  39. knn = KNN(n_neighbors=5)
  40.  
  41. # 将训练集送入knn算法
  42. knn.fit(x_train, y_train)
  43.  
  44. # 预测测试集
  45. y_pred = knn.predict(x_test)
  46.  
  47. # 预测结果展示
  48. labels = ["山鸢尾","虹膜锦葵","变色鸢尾"]   
  49. for i in range(len(y_pred)):
  50.     print("第%d次测试:\t预测值:%s\t\t真实值:%s"%((i+1),labels[y_pred[i]],labels[y_test[i]])) 
  51.  
  52. # 计算准确率
  53. # accuracy_score()函数位于sklearn.metrics模块中，属于Scikit-learn库的一部分
  54. accuracy = accuracy_score(y_test, y_pred) # accuracy_score()函数会比较真实标签值和预测标签值，并计算出准确分类的样本数占总样本数的比例，即准确率。
  55. print("准确率:", accuracy)

运行结果：

  1. 第1次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  2. 第2次测试:	预测值:山鸢尾		真实值:山鸢尾
  3. 第3次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  4. 第4次测试:	预测值:山鸢尾		真实值:山鸢尾
  5. 第5次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  6. 第6次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  7. 第7次测试:	预测值:山鸢尾		真实值:山鸢尾
  8. 第8次测试:	预测值:山鸢尾		真实值:山鸢尾
  9. 第9次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  10. 第10次测试:	预测值:山鸢尾		真实值:山鸢尾
  11. 第11次测试:	预测值:山鸢尾		真实值:山鸢尾
  12. 第12次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  13. 第13次测试:	预测值:山鸢尾		真实值:山鸢尾
  14. 第14次测试:	预测值:山鸢尾		真实值:山鸢尾
  15. 第15次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  16. 第16次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  17. 第17次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  18. 第18次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  19. 第19次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  20. 第20次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  21. 第21次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  22. 第22次测试:	预测值:山鸢尾		真实值:山鸢尾
  23. 第23次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  24. 第24次测试:	预测值:山鸢尾		真实值:山鸢尾
  25. 第25次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  26. 第26次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  27. 第27次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  28. 第28次测试:	预测值:山鸢尾		真实值:山鸢尾
  29. 第29次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  30. 第30次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  31. 第31次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  32. 第32次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  33. 第33次测试:	预测值:虹膜锦葵		真实值:变色鸢尾
  34. 第34次测试:	预测值:山鸢尾		真实值:山鸢尾
  35. 第35次测试:	预测值:山鸢尾		真实值:山鸢尾
  36. 第36次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  37. 第37次测试:	预测值:山鸢尾		真实值:山鸢尾
  38. 第38次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  39. 第39次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  40. 第40次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  41. 第41次测试:	预测值:山鸢尾		真实值:山鸢尾
  42. 第42次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  43. 第43次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  44. 第44次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  45. 第45次测试:	预测值:山鸢尾		真实值:山鸢尾
  46. 准确率: 0.9777777777777777

     2、基于sklearn中的鸢尾花数据集掉包实现knn算法

  1. from sklearn.datasets import load_iris
  2. from sklearn.model_selection import train_test_split, GridSearchCV
  3. from sklearn.preprocessing import StandardScaler
  4. from sklearn.neighbors import KNeighborsClassifier
  5. import numpy as np
  6. import matplotlib.pyplot as plt
  7. import random
  8. from pylab import mpl
  9. # 设置显示中文字体
  10. mpl.rcParams["font.sans-serif"]=["SimHei"]
  11. # 设置正常显示符号
  12. mpl.rcParams["axes.unicode_minus"]=False
  13.  
  14.  
  15. """
  16. 利用KNN算法对鸢尾花进行分类
  17. """
  18.  
  19. # 获取鸢尾花数据 三个类别(山鸢尾/0，虹膜锦葵/1，变色鸢尾/2)，每个类别50个样本，每个样本四个特征值(萼片长度，萼片宽度，花瓣长度，花瓣宽度)
  20. def get_iris_data():
  21.     iris = load_iris()
  22.     iris_data = iris.data # 特征值
  23.     iris_target = iris.target # 目标值(类别)
  24.     return iris_data, iris_target
  25.  
  26. def run():
  27.     # 1.获取鸢尾花的特征值，目标值
  28.     iris_data, iris_target = get_iris_data()
  29.     # 2.将数据分割成训练集和测试集 test_size=0.25表示将25%的数据用作测试集,random_state不同的随机种子会在数据集中抽取不同的20%作为测试集
  30.     x_train, x_test, y_train, y_test = train_test_split(iris_data, iris_target, test_size=0.3,random_state=100)
  31.     # x_train:训练集特征值，x_test:测试集特征值，y_train:训练集目标值，y_test:测试集目标值
  32.         
  33.  
  34.     # 4.knn算法
  35.     knn = KNeighborsClassifier(n_neighbors=5) # 创建一个KNN分类器，n_neighbors默认为5,后续通过网格搜索获取最优参数 
  36.     knn.fit(x_train, y_train) # 将测试集送入算法
  37.     y_predict = knn.predict(x_test) # 获取预测结果
  38.     print(f"预测结果：{y_predict}")
  39.     # 预测结果展示
  40.     labels = ["山鸢尾","虹膜锦葵","变色鸢尾"]   
  41.     for i in range(len(y_predict)):
  42.         print("第%d次测试:\t预测值:%s\t\t真实值:%s"%((i+1),labels[y_predict[i]],labels[y_test[i]]))
  43.     print("准确率：",knn.score(x_test, y_test))
  44.         
  45. get_iris_data()
  46. run()
  47.  
  48.  
  49.  
  50. '''
  51. 运行结果：
  52. 预测结果：[2 0 2 0 2 2 0 0 2 0 0 2 0 0 2 1 1 1 2 2 2 0 2 0 1 2 1 0 1 2 1 1 1 0 0 1 0
  53.  1 2 2 0 1 2 2 0]
  54. 第1次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  55. 第2次测试:	预测值:山鸢尾		真实值:山鸢尾
  56. 第3次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  57. 第4次测试:	预测值:山鸢尾		真实值:山鸢尾
  58. 第5次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  59. 第6次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  60. 第7次测试:	预测值:山鸢尾		真实值:山鸢尾
  61. 第8次测试:	预测值:山鸢尾		真实值:山鸢尾
  62. 第9次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  63. 第10次测试:	预测值:山鸢尾		真实值:山鸢尾
  64. 第11次测试:	预测值:山鸢尾		真实值:山鸢尾
  65. 第12次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  66. 第13次测试:	预测值:山鸢尾		真实值:山鸢尾
  67. 第14次测试:	预测值:山鸢尾		真实值:山鸢尾
  68. 第15次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  69. 第16次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  70. 第17次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  71. 第18次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  72. 第19次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  73. 第20次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  74. 第21次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  75. 第22次测试:	预测值:山鸢尾		真实值:山鸢尾
  76. 第23次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  77. 第24次测试:	预测值:山鸢尾		真实值:山鸢尾
  78. 第25次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  79. 第26次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  80. 第27次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  81. 第28次测试:	预测值:山鸢尾		真实值:山鸢尾
  82. 第29次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  83. 第30次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  84. 第31次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  85. 第32次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  86. 第33次测试:	预测值:虹膜锦葵		真实值:变色鸢尾
  87. 第34次测试:	预测值:山鸢尾		真实值:山鸢尾
  88. 第35次测试:	预测值:山鸢尾		真实值:山鸢尾
  89. 第36次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  90. 第37次测试:	预测值:山鸢尾		真实值:山鸢尾
  91. 第38次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  92. 第39次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  93. 第40次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  94. 第41次测试:	预测值:山鸢尾		真实值:山鸢尾
  95. 第42次测试:	预测值:虹膜锦葵		真实值:虹膜锦葵
  96. 第43次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  97. 第44次测试:	预测值:变色鸢尾		真实值:变色鸢尾
  98. 第45次测试:	预测值:山鸢尾		真实值:山鸢尾
  99. 准确率： 0.9777777777777777
  100. '''

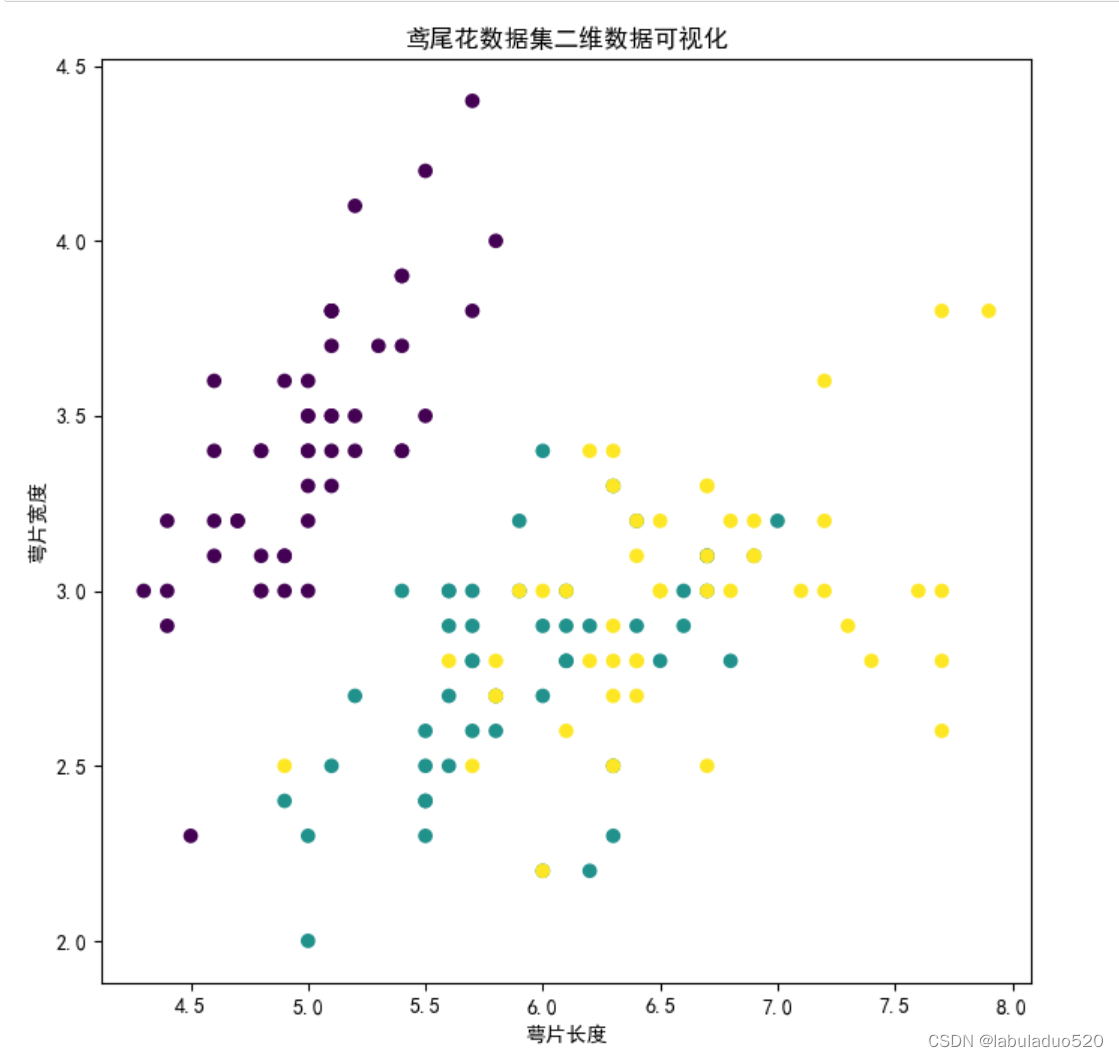
     3、基于sklearn中的鸢尾花数据集掉包实现二维数据可视化

  1. from sklearn.datasets import load_iris
  2. from sklearn.model_selection import train_test_split, GridSearchCV
  3. from sklearn.preprocessing import StandardScaler
  4. from sklearn.neighbors import KNeighborsClassifier
  5. import numpy as np
  6. import matplotlib.pyplot as plt
  7. import random
  8. from pylab import mpl
  9. # 设置显示中文字体
  10. mpl.rcParams["font.sans-serif"]=["SimHei"]
  11. # 设置正常显示符号
  12. mpl.rcParams["axes.unicode_minus"]=False
  13.  
  14. # 获取鸢尾花数据集
  15. iris = load_iris()
  16. x = iris.data[:, :2]  # 只使用前两个特征
  17. y = iris.target
  18.  
  19. # 定义KNN分类器
  20. knn = KNeighborsClassifier(n_neighbors=5)
  21.  
  22. # 将数据集送入算法
  23. knn.fit(x, y)
  24.        
  25. # 可视化数据集
  26. plt.figure(figsize=(8,8),dpi=100) # 创建画布
  27. ''' 
  28. x[:, 0]表示取特征矩阵x的所有行的第一个特征（萼片长度），
  29. x[:, 1]表示取特征矩阵x的所有行的第二个特征（萼片宽度）。
  30. '''
  31. plt.scatter(x[:, 0], x[:, 1], c=y) # 绘制图像 , cmap='coolwarm'
  32. plt.xlabel('萼片长度') # 修改x轴显示
  33. plt.ylabel('萼片宽度') # 修改y轴显示
  34. plt.title('鸢尾花数据集二维数据可视化') # 添加标题
  35. # plt.grid(linestyle='--',alpha=0.5) # 添加网格
  36. plt.show()

运行结果：

      4、基于sklearn中的鸢尾花数据集掉包实现k折交叉验证

k折交叉验证（k-fold cross-validation）是一种常用的模型评估方法，用于评估机器学习模型的性能和泛化能力。它的步骤如下：

①将原始数据集分成k个大小相等的子集（折），其中k-1个子集作为训练集，剩下的1个子集作为验证集。
② 对于每个子集，使用其余的k-1个子集作为训练集来训练模型，然后使用该子集作为验证集来评估模型的性能。
③ 重复步骤2，直到每个子集都充当过一次验证集。
④ 计算k次验证结果的平均值作为模型的性能评估指标。

k折交叉验证的优点：
① 更准确的模型评估：通过对数据集进行多次划分和验证，可以更准确地评估模型的性能和泛化能力。
②充分利用数据：k折交叉验证允许每个样本都充当过训练集和验证集，充分利用了数据集的信息。

k折交叉验证的缺点：
① 计算开销较大：进行k次模型训练和验证比单次训练和验证更加耗时。
② 可能引入一定的方差：由于每次划分的训练集和验证集不同，模型的性能评估结果可能存在一定的方差。

k折交叉验证是一种常用的模型评估方法，可以帮助选择合适的模型和调优模型的参数，提高模型的泛化能力。

  1. from sklearn.datasets import load_iris
  2. from sklearn.model_selection import train_test_split, GridSearchCV,cross_val_score
  3. from sklearn.preprocessing import StandardScaler
  4. from sklearn.neighbors import KNeighborsClassifier
  5. import numpy as np
  6. import matplotlib.pyplot as plt
  7. import random
  8. from pylab import mpl
  9. # 设置显示中文字体
  10. mpl.rcParams["font.sans-serif"]=["SimHei"]
  11. # 设置正常显示符号
  12. mpl.rcParams["axes.unicode_minus"]=False
  13.  
  14. # 获取鸢尾花数据集
  15. iris = load_iris()
  16. x = iris.data
  17. y = iris.target 
  18.  
  19. # 创建KNN分类器
  20. knn = KNeighborsClassifier(n_neighbors=5)
  21.  
  22. # 使用交叉验证评估模型性能
  23. '''
  24. cross_val_score函数用于评估模型在不同训练集上的性能，它会将数据集分成多个子集（称为折），然后在每个子集上进行训练和测试。
  25. cross_val_score函数会返回一个数组，其中包含每个子集的评估结果
  26. '''
  27. scores = cross_val_score(knn, x, y, cv=5)  # 5折交叉验证
  28.  
  29. # 输出每次交叉验证的准确率
  30. print("每次交叉验证的准确率:", scores) 
  31.  
  32. # 输出平均准确率和标准差
  33. print("平均准确率:", np.mean(scores))
  34. print("准确率标准差:", np.std(scores))
  35.  
  36.  
  37. '''
  38. 运行结果：
  39. 每次交叉验证的准确率: [0.96666667 1.         0.93333333 0.96666667 1.        ]
  40. 平均准确率: 0.9733333333333334
  41. 准确率标准差: 0.02494438257849294
  42. '''
  • 优缺点分析

优点：

1. 简单直观：KNN算法的思想简单明了，易于理解和实现。

2. 无需训练过程：KNN是一种基于实例的学习方法，不需要显式地进行训练，而是根据训练数据集直接进行预测。

3. 对数据分布没有假设：KNN算法对数据分布没有假设，适用于各种类型的数据。

4. 可以进行多分类：KNN算法可以处理多分类问题，并且在类别不平衡的情况下也能有效工作。

缺点：

1. 计算复杂度高：KNN算法需要计算测试样本和所有训练样本之间的距离，当样本规模较大时，计算复杂度较高。

2. 存储开销大：KNN算法需要保存所有的训练样本，对内存要求较高。

3. 预测速度慢：由于需要计算距离并比较所有训练样本，KNN算法的预测速度相对较慢。

4. 对异常值敏感：KNN算法对异常值敏感，如果训练集中有噪声或异常值，可能会对预测结果产生较大影响。

5. 需要确定K值：KNN算法中的K值需要人为设定，选择不当可能导致预测结果不准确。

总的来说，KNN算法是一种简单易懂、灵活、适用于多分类问题的算法，但在计算和存储开销、预测速度等方面存在一些缺点。

声明：本文内容由网友自发贡献，不代表【wpsshop博客】立场，版权归原作者所有，本站不承担相应法律责任。如您发现有侵权的内容，请联系我们。转载请注明出处：https://www.wpsshop.cn/w/Cpp五条/article/detail/703043
推荐阅读
相关标签

Copyright © 2003-2013 www.wpsshop.cn 版权所有，并保留所有权利。

  

闽ICP备14008679号