LIS-最长上升子序列

LIS(最长上升子序列)是一个经典的问题。

首先我们来介绍子序列的概念：

子序列指的是一个序列中，按照原顺序选出若干个不一定连续的元素所组成的序列。

LIS有两种算法模型：一种是复杂度为的dp模型，另外一种是复杂度为,利用二分实现的模型。

模型一：复杂度为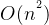的dp模型

我们首先定义状态:
我们定义为以结尾的最长上升子序列长度。
设置 为小于  的某一点，那么当  时，必然有，以 结尾的最长上升子序列,现在能以 结尾，并且长度。
因为且 ，满足上升子序列的要求。
所以 的一条转移路径为
但是  是比小的某一个值，所以转移到 这一状态的值很多，我们要选择最优状态。所以 的状态转移:
;
那么当 时
此时肯定不满足上升子序列，所以 与 毫无关联。
由此我们可以写出 LIS 的算法：

#include<bits/stdc++.h>
using namespace std;
 
using ll = long long;
const int N=1e3+10;
int n;
ll a[N],dp[N];
int main()
{
  cin>>n;
  for(int i = 1;i <= n;i++) {
    cin >> a[i];
    dp[i]=1;
  }
  
  for(int i = 1;i <= n;i++)
  {
    for(int j = 1;j < i;j++)
      {
      if(a[i] > a[j]) dp[i]=max(dp[i],dp[j]+1);
      }
  }
  ll ans = 0;
  for(int i = 1; i <= n; i++){
    ans = max(ans,dp[i]);
  }  
  cout<<ans<<endl;
  return 0;
 }

模型二：复杂度为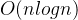,利用二分实现的模型。

当数据量较大，使用常规的的LIS算法会超时
故采用二分+贪心的算法求解： 
维护一个数组，表示长度为  的最长上升子序列的末尾元素
使用贪心思想来对数组进行更新，核心思想是末尾元素越小，越容易凑出最长的子序列
遍历每一个元素，若当前元素比更大，则直接加入数组的末尾 
若当前元素小于,则从数组中找到一个大于等于它的最小值将其替换
由于数组是递增的，故使用二分算法进行搜索和替换
最终输出数组的长度即为答案 。

注意此算法的缺陷：数组只有长度是有意义的，其保存的元素是无意义的。

由此我们可以写出 LIS 的算法：

#include<bits/stdc++.h>
using namespace std;
 
using ll = long long;
const int N = 3e5 + 10;
ll a[N],low[N];
 
int main(){
  int n,length = 1;
  cin >> n;
  for(int i = 1; i <= n; i++){
    cin >> a[i];
  }
  low[1] = a[1];  //初始化，长度为1的子序列初始化为第一个元素 
  for(int i = 2; i <= n; i++){
    if(a[i] > low[length]){  //若当前元素大于low数组末尾元素，直接插入 
      low[++length] = a[i];  
    }else{   //若小于，则用low数组中刚好大于等于它的元素替换之 
      int index = lower_bound(low + 1, low + length + 1,a[i]) - low;  //获取插入位置下标 
      low[index] = a[i];  //替换 
    }
  }
  cout << length <<endl;  //输出low数组长度即为答案 
  return 0;
}