机器学习-线性回归

实现原理

假设:我们可以用一个函数来模仿,现在数据的走势,比如以下的数据,假设我们有一个函数可以拟合,一下数据(红线).

我们先定义一个简单的函数,比如说是一元线性回归:
h: 表示我们预测的值
x: 变量
而我要求的就是这些参数.

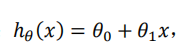
但是如何能够准确的让我们模拟的函数准确呢?

我们再这里就利用了数学上的平方误差公式,然后利用方差公式,在求平方误差值最小的时候,我们的参数就是当前好的参数.
所以这里就引出了代价函数

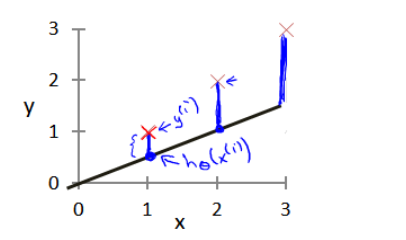
我们看红色X (真实值)距离我们自己画的函数有多远,尽量的让自己画的函数,能够挨着,真实值为最近.
(如何实现它能够尽量的接近呢? 我们就定义代价函数 – 基本的原理也是 真实值 与我们预测值的距离 之和 的平均值 ,)

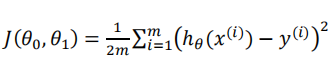
注意: 上面之所以多除2 是因为后面比较好计算.

然后我们是怎么计算到这些值的呢?
就是求我们的代价函数最小值.
按数学的逻辑来说,我们就是要对我们的代价函数求导,要找到它的最小值,但是计算机如何做呢?

梯度下架

之前我们说了,要求代价函数的最小值,我们如何求呢?

现在 就可以说了 ,我们是利用梯度下降算法来求到代价函数的最小值.

我们对代价函数求偏导,就能够得到梯度方向,然后就可以选择学习速率