神经网络的知识蒸馏（Distilling the Knowledge in Neural Network）_神经网络蒸馏

论文链接
原博客参考： 链接

1. 背景

在训练过程中，我们需要使用复杂的模型，大量的计算资源，以便从非常大、高度冗余的数据集中提取出信息。在实验中，效果最好的模型往往规模很大，甚至由多个模型集成得到。而大模型不方便部署到服务中去，常见的瓶颈如下:
（1）推理速度慢
（2）对资源部署的要求高
因此，模型压缩（在保证性能的前提下减少模型的参数量）成为了一个重要的问题。而”模型蒸馏“属于模型压缩的一种方法。

举一个比较形象的例子：
模型就像一个容器，训练数据中蕴含的知识就像是要装进容器里的水。当数据知识量(水量)超过模型所能建模的范围时(容器的容积)，加再多的数据也不能提升效果(水再多也装不进容器)，因为模型的表达空间有限(容器容积有限)，就会造成underfitting；而当模型的参数量大于已有知识所需要的表达空间时(容积大于水量，水装不满容器)，就会造成overfitting，即模型的variance会增大(想象一下摇晃半满的容器，里面水的形状是不稳定的)。

模型参数两和模型捕获的“知识量”之间的关系：
（1）模型的参数量和其所能捕获的“知识”量之间并非稳定的线性关系，其增长曲线如下所示：

（2）完全相同的模型架构和模型参数量，使用完全相同的训练数据，能捕获的“知识”量并不一定完全相同，另一个关键因素是训练的方法。合适的训练方法可以使得在模型参数总量比较小时，尽可能地获取到更多的“知识”(上图中的3与2曲线的对比)。

2.理论依据

1. 教师学生模型

Teacher Model是知识的输出者，Student Model是知识的接受者。
（1）原始模型的训练（教师模型）
训练教师模型Net-T，其特点是模型相对复杂，模型参数量大。唯一要求，对于输入X，都可以输出Y，其输出值对应相应类别的概率。
（2）精简模型训练（学生模型）
训练学生模型Net-S，它是参数量较小，模型结构相对简单的单模型。对于输入X，输出对应的Y，Y经过softmax映射之后同样能够输出对应类别的概率值。

2.知识蒸馏关键点

现实中，由于我们不可能收集到某问题的所有数据来作为训练数据，并且新数据总是在源源不断的产生，因此我们只能退而求其次，训练目标变成在已有的训练数据集上建模输入和输出之间的关系。由于训练数据集是对真实数据分布情况的采样，训练数据集上的最优解往往会多少偏离真正的最优解(这里的讨论不考虑模型容量)。
在知识蒸馏时，由于我们已经有了一个泛化能力较强的Net-T，我们在利用Net-T来蒸馏训练Net-S时，可以直接让Net-S去学习Net-T的泛化能力。
一个很直白且高效的迁移泛化能力的方法就是：使用softmax层输出的类别的概率来作为“soft target”。

• KD训练过程和传统训练过程相对比
  （1）传统training过程(hard targets): 对ground truth求极大似然
  （2）KD的training过程(soft targets): 用large model的class probabilities作为soft targets
  例子：
  在手写数字中，输出类别有10个：
  
  假设某个输入的“2”更加形似"3"，softmax的输出值中"3"对应的概率为0.1，而其他负标签对应的值都很小，而另一个"2"更加形似"7"，"7"对应的概率为0.1。这两个"2"对应的hard target的值是相同的，但是它们的soft target却是不同的，由此我们可见soft target蕴含着比hard target多的信息。并且soft target分布的熵相对高时，其soft target蕴含的知识就更丰富。
  这就解释了为什么通过蒸馏的方法训练出的Net-S相比使用完全相同的模型结构和训练数据只使用hard target的训练方法得到的模型，拥有更好的泛化能力。

3. softmax函数

原始softmax函数：
$q_i=\frac{exp(z_i)}{{\sum }_{j}exp(z_j)}$
直接使用softmax层输出值作为soft target，这又会带来一个问题: 当softmax输出的概率分布熵相对较小时，负标签的值都很接近0，对损失函数的贡献非常小，小到可以忽略不计。因此"温度"这个变量就派上了用场。
下面公式是加了温度之后softmax函数：
$q_i=\frac{exp(z_i/T)}{{\sum }_{j}exp(z_j/T)}$

这里的T就是温度，当T=1，就是原来的softmax函数，T越大，softmax越大，其分布的熵越大，负标签也会被相应放大，模型训练的时候就更加关注负标签。

3. 知识蒸馏的具体方法

1.通用的知识蒸馏方法

第一步，训练教师网络Net-T
第二步，在高温下，蒸馏Net-T的知识到Net-S

第一步，训练Net-T过程跟平常训练没什么区别
第二步，高温蒸馏过程
目标函数：$L=\alpha L_{soft}+\beta L_{hard}$

• $v_i:$ Net-T的logits输出
• $z_i:$ Net-S的logits输出
• $p_i^T:$ Net-T的在温度=T下的softmax输出在第i类上的值
• $c_i:$在第i类上的ground truth值, c i ∈ { 0 , 1 } c_i \in {\{0,1\}} ci​∈{0,1}，正标签取1，负标签取0
• $N:$总标签数量
  所以软标签loss为：
  
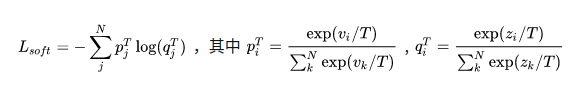
  硬标签loss：
  
  硬标签loss的理解：Net-T也有一定的错误率，使用ground truth可以有效降低错误被传播给Net-S的可能。打个比方，老师虽然学识远远超过学生，但是他仍然有出错的可能，而这时候如果学生在老师的教授之外，可以同时参考到标准答案，就可以有效地降低被老师偶尔的错误“带偏”的可能性。

2. 关于温度T的讨论

温度T的特点：