- 1spark ml实现逻辑回归案例分析_sparkml 输出逻辑回归的变量系数
- 2Go C画图 CSP-J 信息学奥赛 2023.02.16 测试题_粤港澳青少年信息学创新大赛 图形化编程 真题
- 3将 Llama 3 与 Ollama 和 Python 结合使用 使用 Ollama API 访问这一领先模型_python 调用本地部署的llama3
- 4AI、AGI、AIGC、ChatGpt 理解_什么是agi ugi
- 5DW金融风控-task02数据分析_dw金融软件
- 6前后端分离的后台管理系统源码,快速开发OA、CMS网站后台管理、毕业设计项目
- 7服务器不支持PUT和DELETE请求处理_麒麟服务器不支持put请求
- 8FreeRTOS移植到STM32-任务的创建
- 9二、图形数据库Neo4j的简介与安装_neo4j是什么公司研发的
- 10一篇博客带你领略学习Python的第三方库---如何获取和安装第三方库,关于三种常见第三方库的下载和讲解(pyinstall库,jieba库,wordcloud库),更多第三方库的分类介绍_python第三方库
数据挖掘与机器学习实验-线性回归【机器学习实验】[广州大学]- python实现_【实验原理】 本实验旨在介绍数据挖掘中的回归模型算法及其应用。通过使用python
赞
踩
一、实验目的
本实验课程是计算机、人工智能、软件工程等专业学生的一门专业课程,通过实验,帮助学生更好地掌握数据挖掘与机器学习相关概念、技术、原理、应用等;通过实验提高学生编写实验报告、总结实验结果的能力;使学生对机器学习模型、算法等有比较深入的认识。要掌握的知识点如下:
- 掌握机器学习中涉及的相关概念、模型、算法;
- 熟悉机器学习模型训练、验证、测试的流程;
- 熟悉常用的数据预处理方法;
- 掌握线性回归优化问题的表示、求解及编程。
二、基本要求
- 实验前,复习《数据挖掘与机器学习》课程中的有关内容。
- 准备好实验数据,编程完成实验内容,收集实验结果。
- 独立完成实验报告。
三、实验软件
推荐使用Python编程语言(允许使用numpy库,需实现详细实验步骤,不允许直接调用scikit-learn中关于回归、分类等高层API)。
四、实验内容:
基于California Housing Prices数据集,完成关于房价预测的线性回归模型训练、测试与评估。
- 准备数据集并认识数据
下载California Housing Prices数据集https://www.kaggle.com/camnugent/california-housing-prices
了解数据集各个维度特征及预测值的含义 - 探索数据并预处理数据
观察数据集各个维度特征及预测值的数值类型与分布
预处理各维度特征(如将类别型维度ocean_proximity转换为one-hot形式的数值数据),参考:https://blog.csdn.net/SanyHo/article/details/105304292
划分70%的样本作为训练数据集,30%的样本作为测试数据集 - 求解模型参数
编程实现线性回归模型的闭合形式参数求解
编程实现线性回归模型的梯度下降参数优化 - 测试和评估模型
在测试数据集上计算所训练模型的R2指标
五、学生实验报告
(1)简要介绍线性回归闭合形式参数求解的原理
首先有
a. 假设函数:
b. 参数:
c. 损失函数:
d. 优化目标:
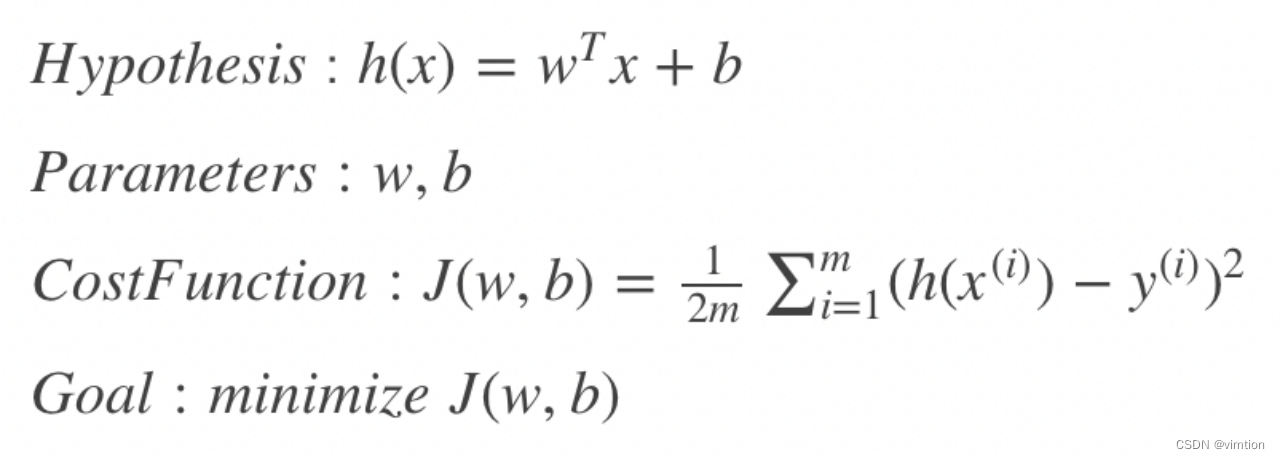
m个样本,d维特征。为了计算简便,通常把w,b统一起来,给x增加一列1,b作为w0,有:
对于目标有
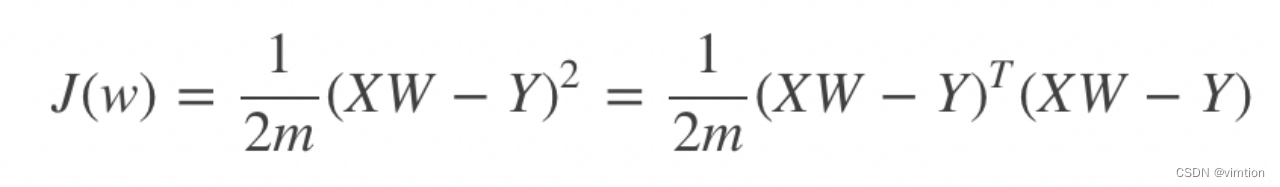
求导得
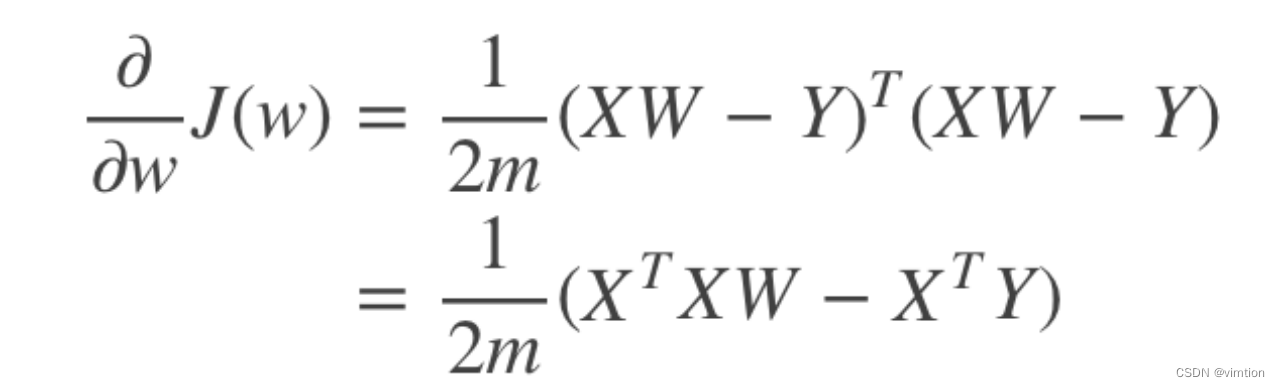
令导数为0

(2)简要介绍线性回归梯度下降参数求解的原理
定义损失函数为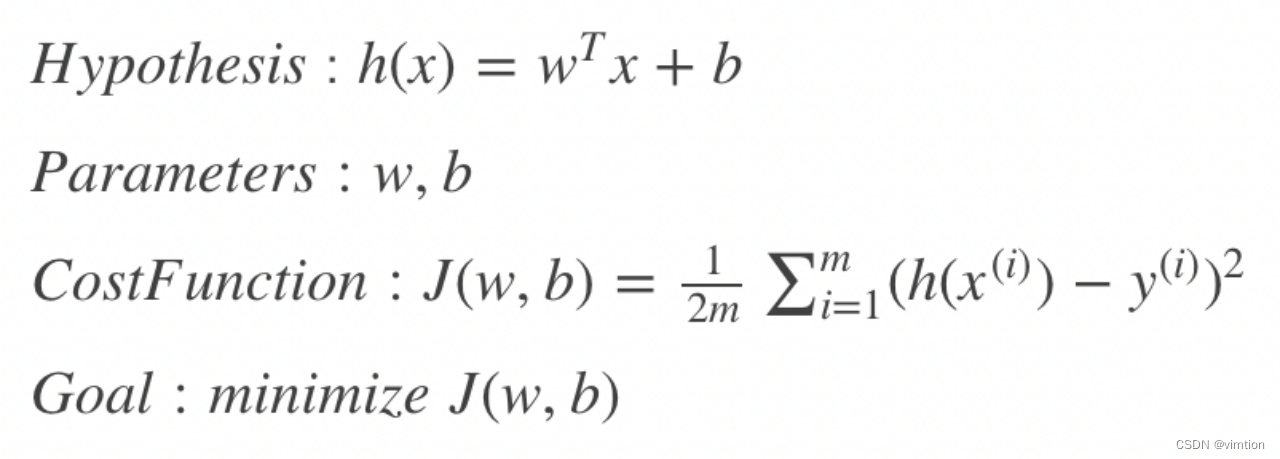
对J(w,b) 计算偏导得
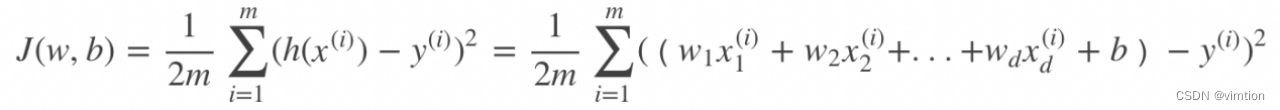
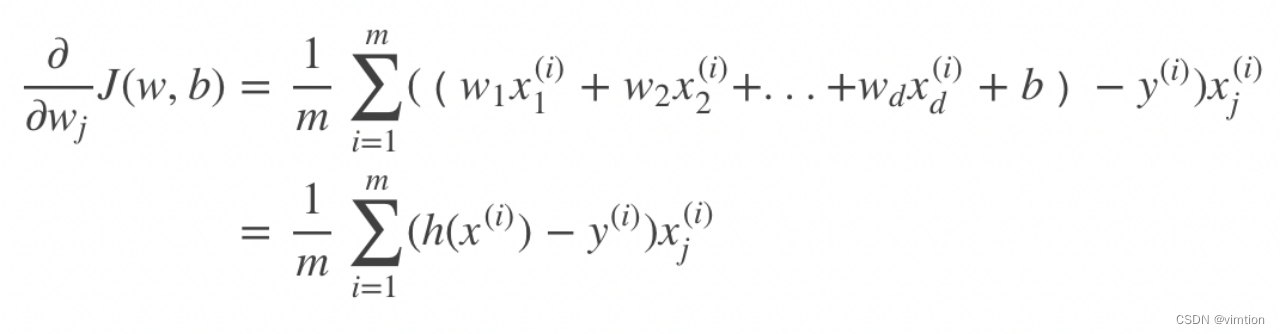
参数按照如下进行更新
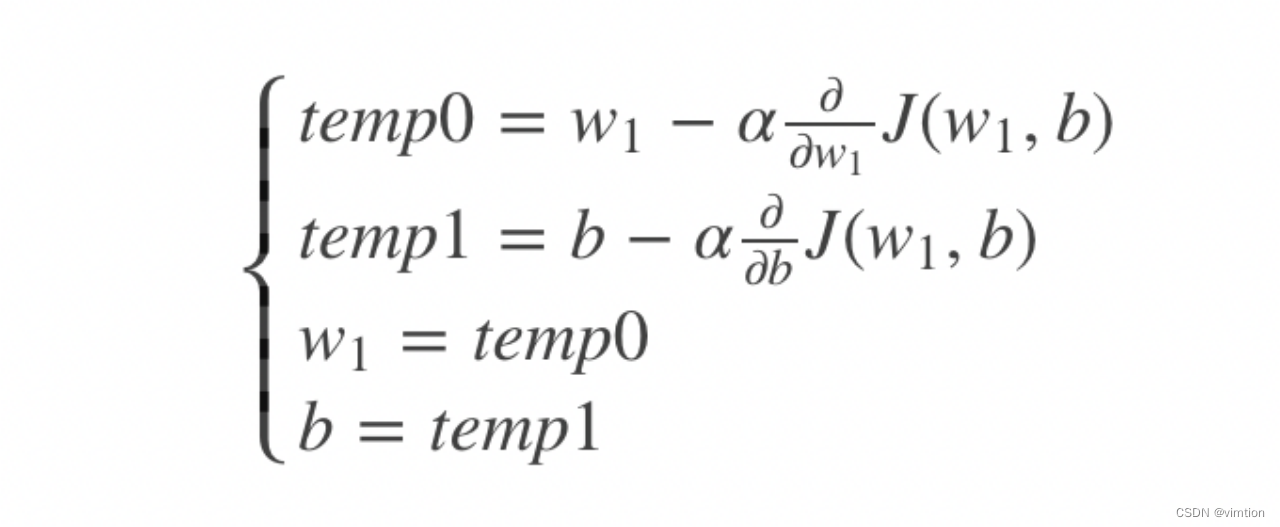
最后得到参数theta,最后使用模型进行预测。
(3)程序清单(包含详细求解步骤)
(a)读取数据并查看数据组成
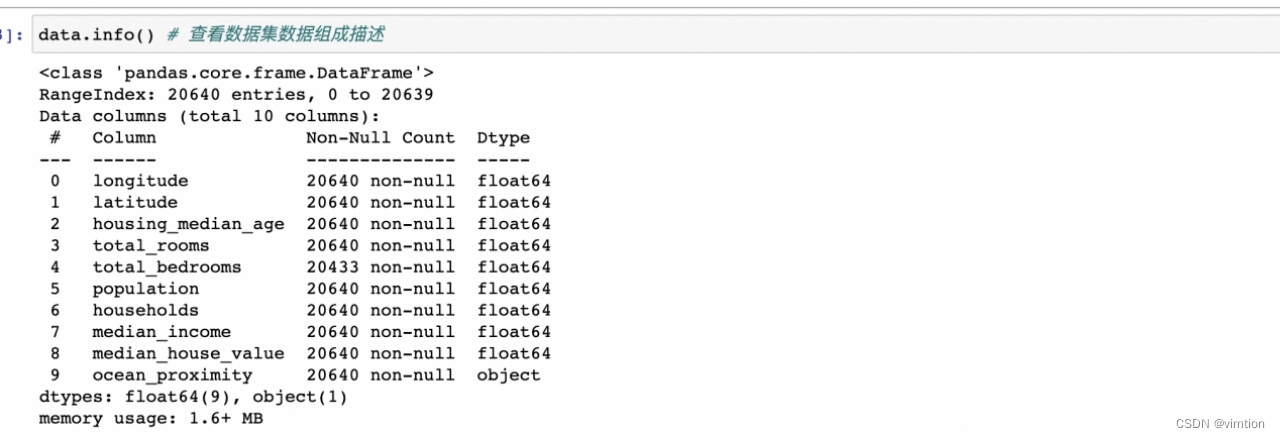
从这里可以看到数据有9个feature,8个类型为浮点其中有一个为文本。而对于文本数据,则需要进行OneHot编码。
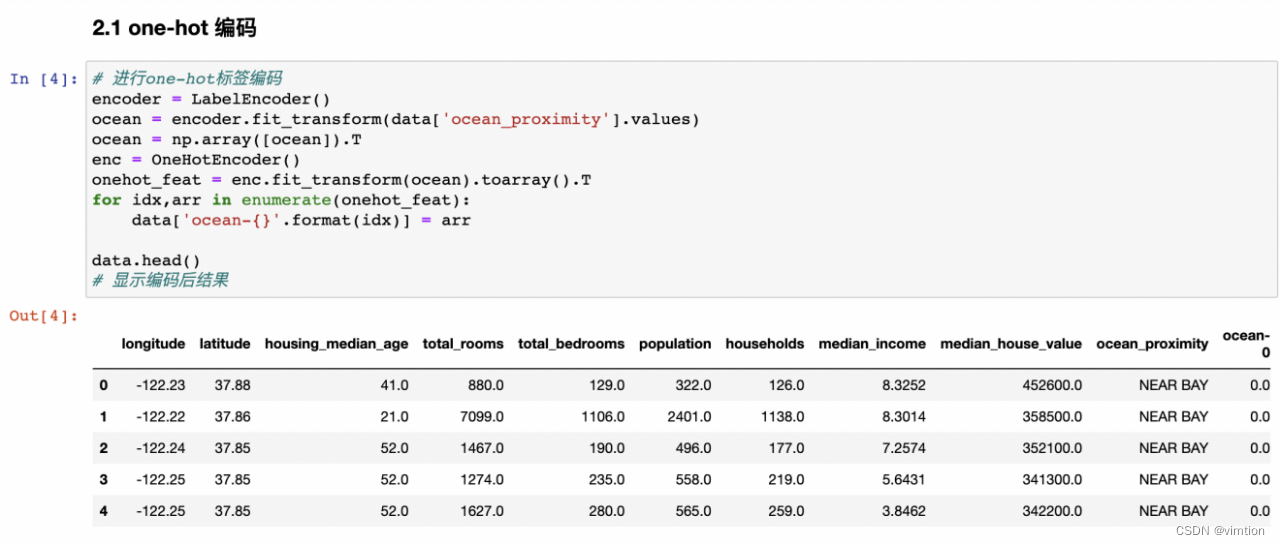
(b)对文本进行onehot编码。
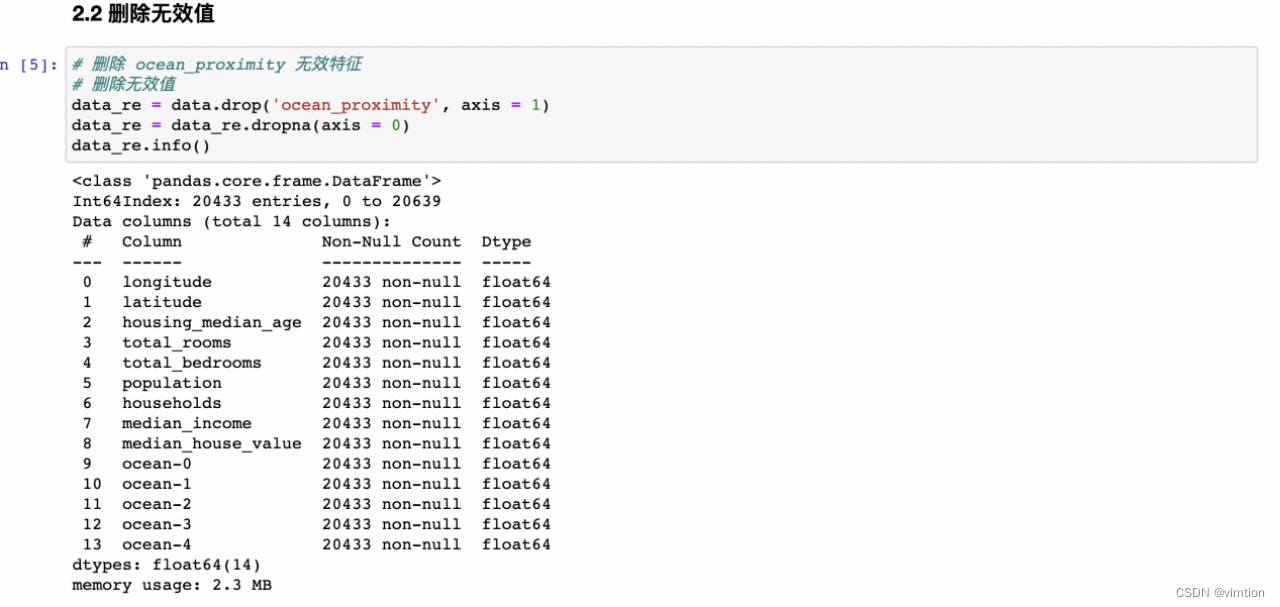
©删除无效值
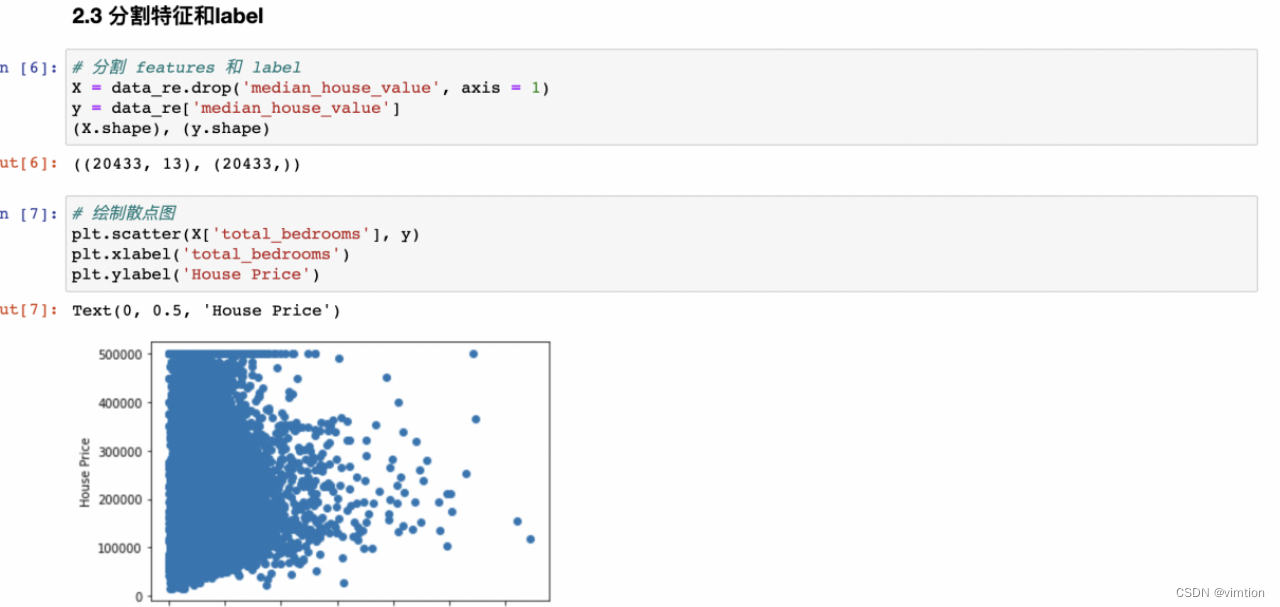
这时候数据的预处理基本已经完成,接下来可以对features和label进行分割。
(d)分割特征和label
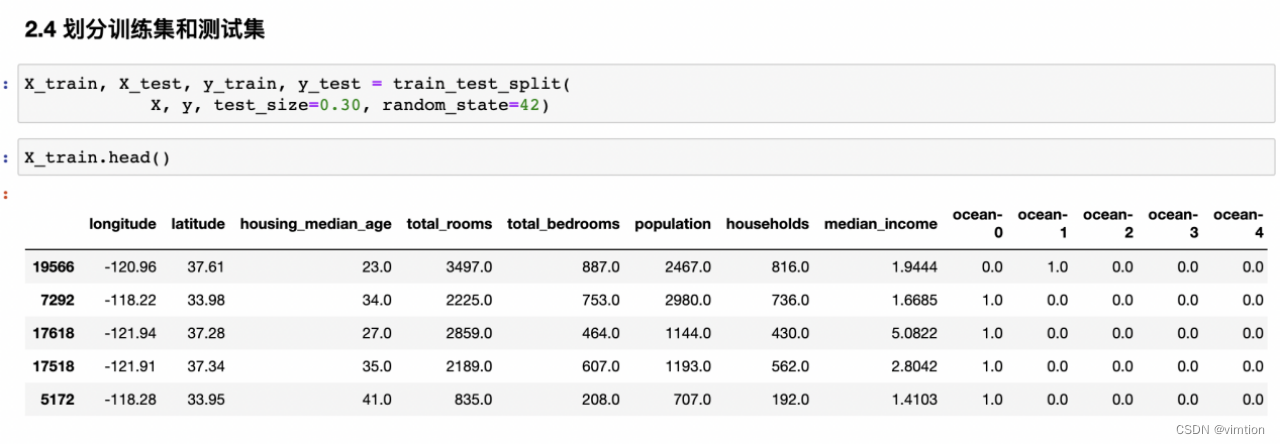
(e)划分训练集和测试集
按照3:7划分训练集和测试集
(f)训练模型
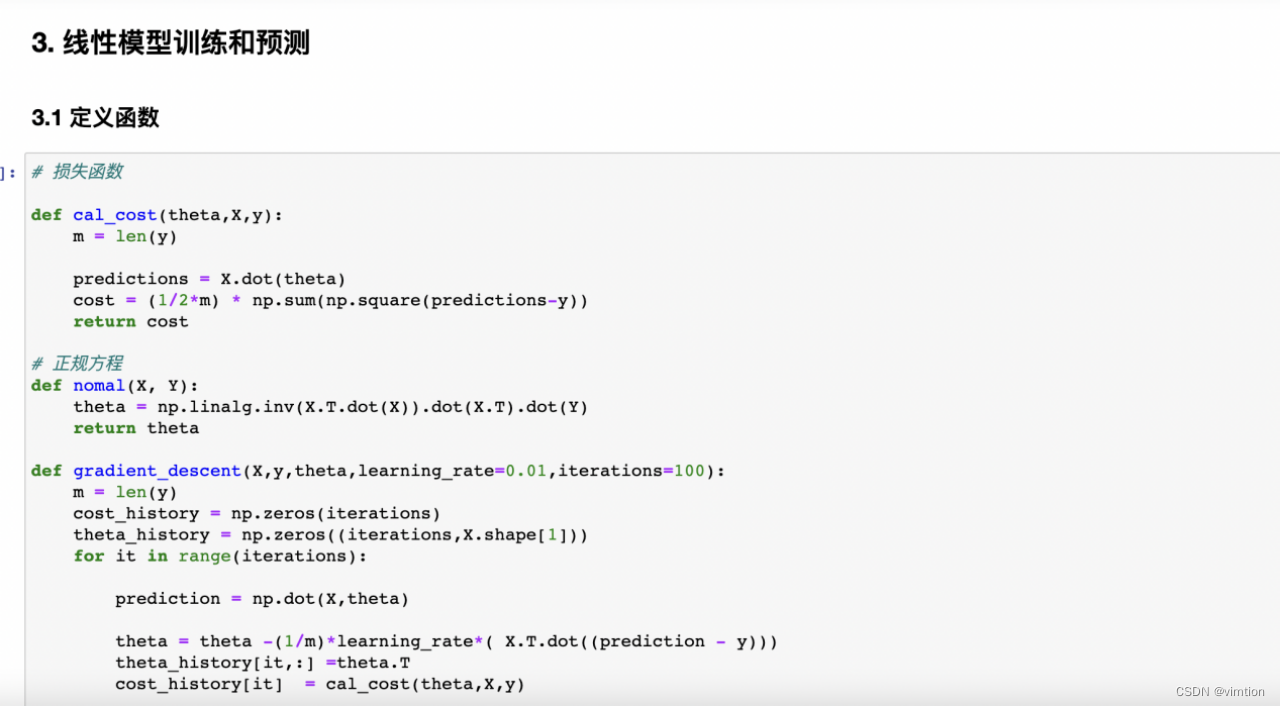
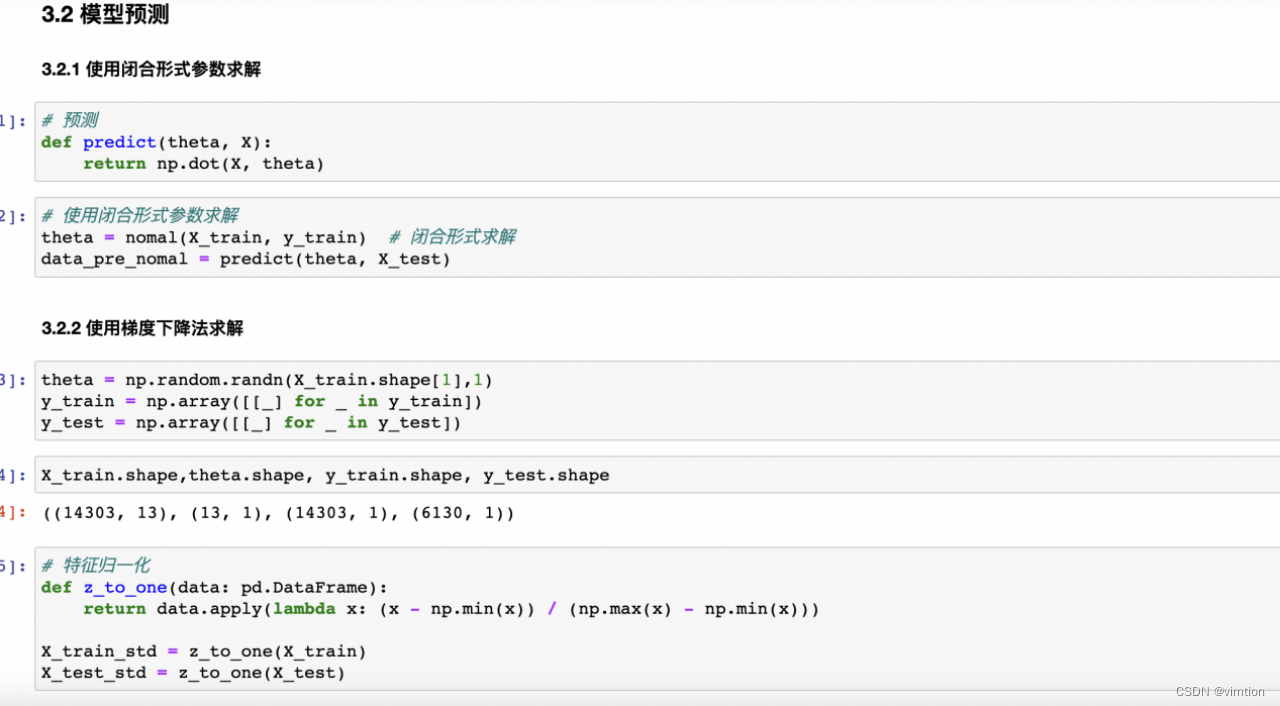
为了达到更好的训练效果,梯度下降的实现需要进行特征归一化。
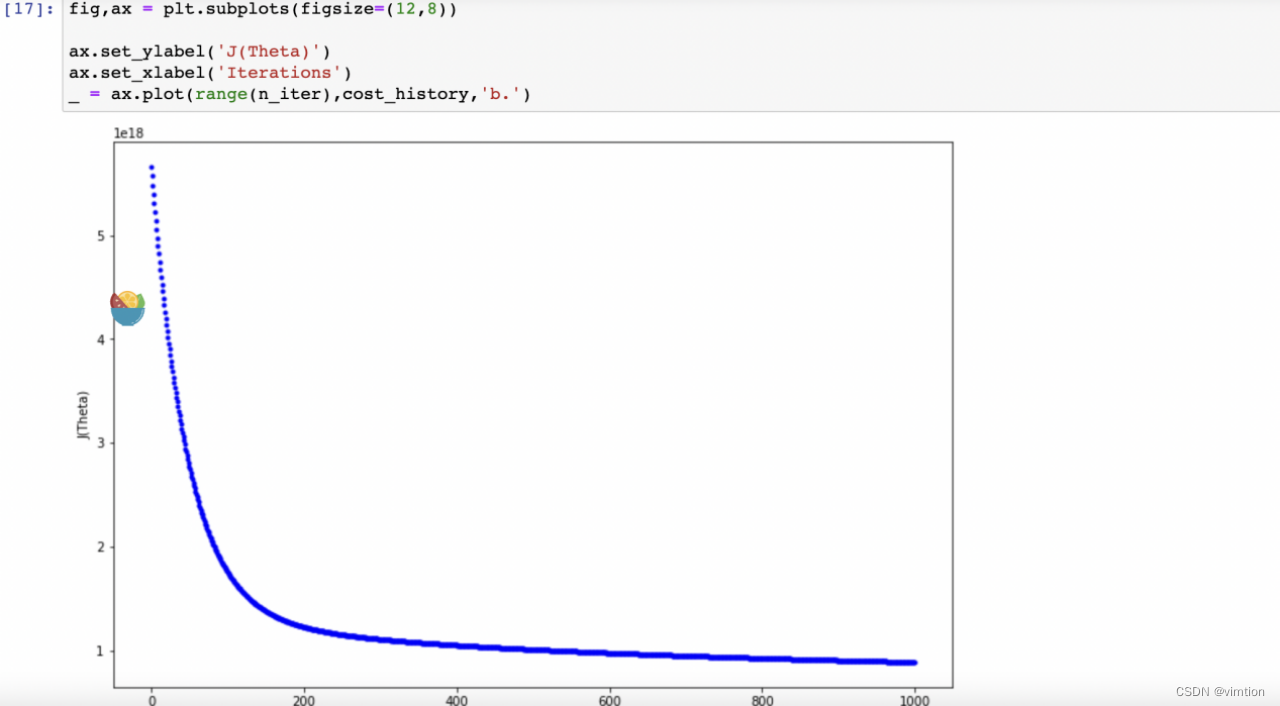
通过查看损失函数和迭代次数的曲线,可以得知模型已经接近收敛。
(g)展示分别通过闭合形式参数和梯度下降预测的结果
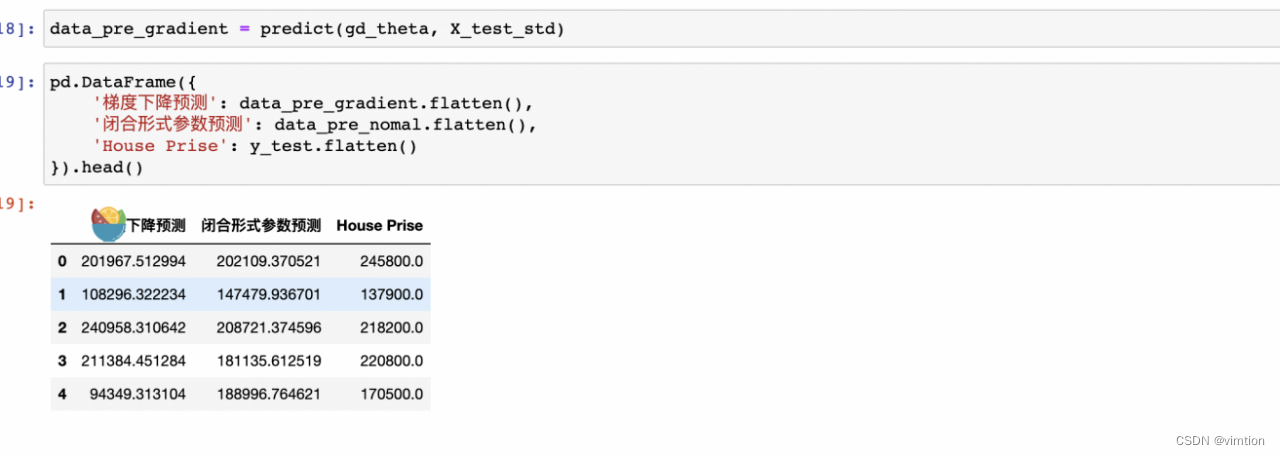
(h)通过R2评估模型
根据预测的结果可以得知,使用正规方程的方法比梯度下降的效果更好。
(4)展示实验结果,比较两种求解方式的优劣
**在这次实验中,使用正规方程等方法比梯度下降更佳。**通过实验,总结出两种不同方法的特性。一般,当特征维数比较小时,正规方程计算是一个很好的方法,当特征维数比较多的时候,通常采用梯度下降方法。对复杂的模型来说,求导过程可能相当复杂,只能用梯度下降法不断向最优解处逼近。对于模型而言,往往超过10000维度则可以视为维度高,这时候也可以引入PCA降维等方法。
| 梯度下降 | 正规方程 |
|---|---|
| 需要多次选择学习率 | 不需要选择学习率,不用迭代 |
| 需要多次迭代 | 需要计算(XTX)-1 |
| 当特征维度很大仍然适用 | 特征维度大时运行会比较慢 |
(5)讨论实验结果,分析各个特征与目标预测值的正负相关性
从结果上看,median_income特征与房价正相关,并且影响最大。
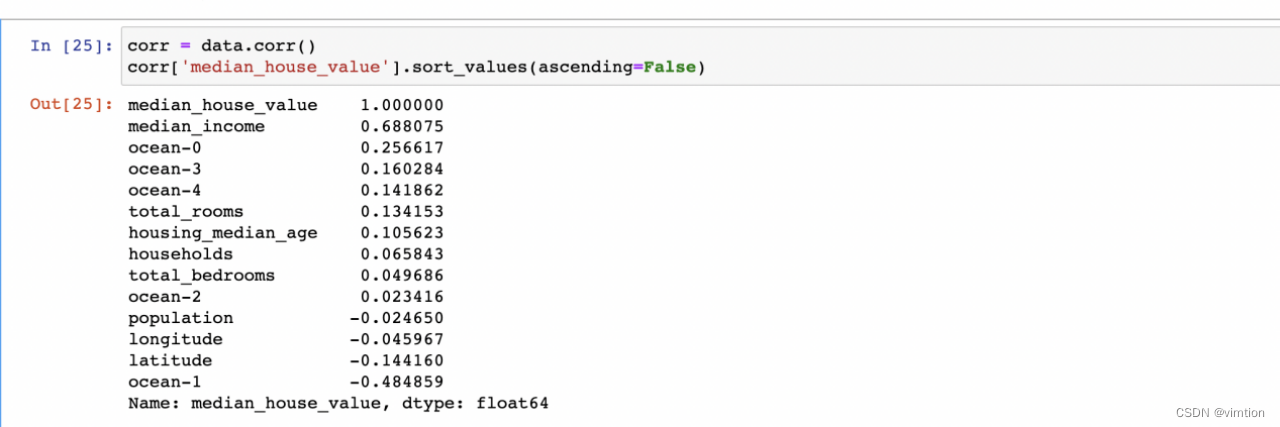
从结果上看,median_income特征与房价正相关,并且影响最大。



