使用格拉姆角场(GAF)将时间序列转换为图像的逆变换_gasf图像的主对角线

在学习《Imaging Time-Series to Improve Classification and Imputation》的过程中，我产生了一个疑问，即如何从获得的格拉姆和/差角场(GASF/GADF)中，重构原始的时间序列？即时间序列转图像变换的逆变换。

将时间序列转换为GASF/GADF的过程，参考了这篇文章，使用了pyts库实现：

用python将时间序列信号或一维数组 转化成 图像的几种方法_特征不对应的时间序列数据怎么转图像-CSDN博客

但在从GASF/GADF重构时间序列的过程中，遇到了困难。论文原文中表示：

从主对角线中，可以重构时间序列。

于是我参考了这篇文章的方法：

格拉姆矩阵逆变换_麋鹿不迷路11的博客-CSDN博客

感谢作者给我的启发，经过计算，在GASF中：

，其中  表示GASF， 表示最大最小值标准化后的原始时间序列。

在GADF中，上述文章的结果有误，应为：

因此，可以通过反向计算时间序列的值。但是这种方式得到的时间序列的值无法区分正负号。为了正确地重构，可以在构建GASF时，使用参数 sample_range=(0, 1)。而默认的 sample_range 是 (-1,1)，这样 GramianAngularField 内部会使用 MinMaxScaler(sample_range=self.sample_range) 将原始的时间序列标准化到 [0,1] 之间，为非负数，因此可以没有歧义地重构。代码为：

gasf = GramianAngularField(image_size=image_size, method='summation', sample_range=(0, 1))
X_gasf = gasf.fit_transform(X)

补充完整的代码和重构后的结果，生成GASF/GADF并使用GASF重构原始数据：

# In[] Data
X = [10,8,6,4,2,0.5,2,0.5,2,4,6,8,7,8,6,4,2,2.5,0,1,1.5,3.5,5.5,7.5,9.5]
X = np.array(X)
X = X.reshape(1, -1)
# In[] Transform the time series into Gramian Angular Fields
import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.axes_grid1 import ImageGrid, make_axes_locatable
from pyts.image import  GramianAngularField
 
image_size = 10
gasf = GramianAngularField(image_size=image_size, method='summation', sample_range=(0, 1))
X_gasf = gasf.fit_transform(X)
gadf = GramianAngularField(image_size=image_size, method='difference', sample_range=(0, 1))
X_gadf = gadf.fit_transform(X)
 
# Show the results for the first time series
plt.figure(figsize=(5, 10))
axs = plt.subplots()
plt.subplot(211)
plt.imshow(X_gasf[0], cmap='rainbow', origin='lower')
plt.title("GASF", fontsize=16)
plt.subplot(212)
plt.imshow(X_gadf[0], cmap='rainbow', origin='lower')
plt.title("GADF", fontsize=16)
 
cax = plt.axes([0.7, 0.1, 0.02, 0.8])
plt.colorbar(cax = cax)
plt.suptitle('Gramian Angular Fields', y=0.98, fontsize=16)
plt.tight_layout()
plt.show()
# In[] Inverse transformation
x = X.reshape(-1)
y = np.array([X_gasf[0, i, i] for i in range(image_size)]) # main diagonal
x_rec = np.sqrt( (y+1) /2)
 
plt.suptitle('GASF Inverse')
plt.subplot(211)
plt.plot(x, label='x')
plt.legend()
plt.subplot(212)
plt.plot(x_rec, label='x_rec')
plt.legend()
plt.show()

重构的结果：

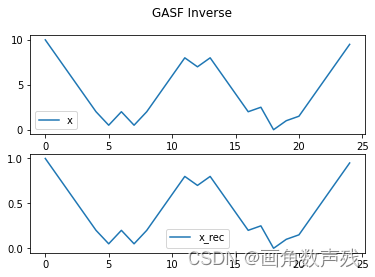
可以看到，重构后的结果已经被标准化到 [0,1] 之间。这里的 image_size=25，与原始数据长度相等。如果采用更小的 image_size，则不能准确地重构原始数据，以下是 image_size=10 的重构结果：

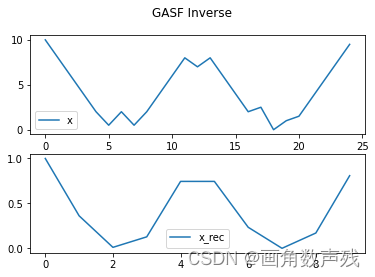
关于如何在保持 [-1,1] 取值范围的情况下重构原始数据，只有一些个人的不成熟的想法，仅做参考~

参考原文中的公式：

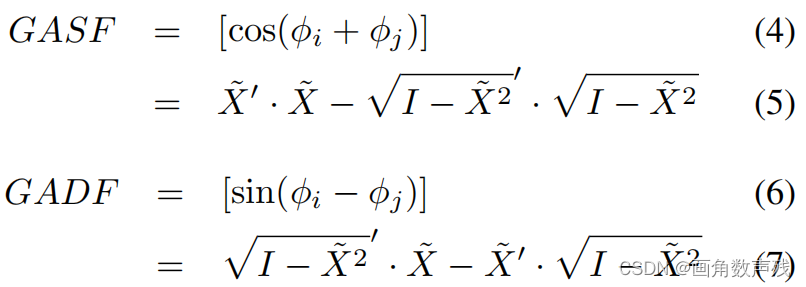
也就是说GASF的值可以很简单地理解为两角之和的余弦，GADF是两角之差的正弦。此时，如果使用者已经知道了某个  的角度()为 0，那么就可以消去一个变量，将上述两个公式换算为同一个角的正弦值和余弦值，也就可以使用 GASF/GADF 第 i 行(列)的值计算出原始值了。但这里的  也是指的 MinMax 之后的值，因此使用者不一定能确定具体哪个值准确是 0 ，因为 MinMax 的步骤包含在 GramianAngularField 的内部：

    def transform(self, X):
        """Transform each time series into a GAF image.
        Parameters
        ----------
        X : array-like, shape = (n_samples, n_timestamps)
        Returns
        -------
        X_new : array-like, shape = (n_samples, image_size, image_size)
            Transformed data. If ``flatten=True``, the shape is
            `(n_samples, image_size * image_size)`.
        """
        X = check_array(X)
        n_samples, n_timestamps = X.shape
        image_size = self._check_params(n_timestamps)
 
        paa = PiecewiseAggregateApproximation(
            window_size=None, output_size=image_size,
            overlapping=self.overlapping
        )
        X_paa = paa.fit_transform(X)
        if self.sample_range is None:
            X_min, X_max = np.min(X_paa), np.max(X_paa)
            if (X_min < -1) or (X_max > 1):
                raise ValueError("If 'sample_range' is None, all the values "
                                 "of X must be between -1 and 1.")
            X_cos = X_paa
        else:
            scaler = MinMaxScaler(sample_range=self.sample_range)
            X_cos = scaler.fit_transform(X_paa)
        X_sin = np.sqrt(np.clip(1 - X_cos ** 2, 0, 1))
        if self.method in ['s', 'summation']:
            X_new = _gasf(X_cos, X_sin, n_samples, image_size)
        else:
            X_new = _gadf(X_cos, X_sin, n_samples, image_size)
 
        if self.flatten:
            return X_new.reshape(n_samples, -1)
        return X_new

使用 sample_range=None，可以跳过这个步骤，并可以在外部提前进行 MinMax。同时，还需要关注 PiecewiseAggregateApproximation 函数的执行，它会对原始数据进行一些下采样，同样也可能使用户提前预设好的 0 值被改变。因此，将时间序列的第一个值或最后一个值设置（添加）为0 可能更合适。这样就手动地获得了一个为 0 的角度。

但这样也不能保证是无损地恢复，float 类型的存在和 arg 三角函数运算都可能造成微小的误差。欢迎大佬指正，如果有更好的方案请不要怕麻烦地拍砖~

初学 GAF，数学也不太好，谢谢参考~