2023面试高手

这个屌丝很懒，什么也没留下！

热门标签

ACM集训周记（三）_设r={ r1, r2 , …, rn}是要进行排列的n个小写字母。其中小写字母r1, r2 , …

作者：2023面试高手 | 2024-04-02 19:59:35

踩

设r={ r1, r2 , …, rn}是要进行排列的n个小写字母。其中小写字母r1, r2 , …, rn

DFS类

问题 A: 全排列问题

题目描述

输出自然数1到n所有不重复的排列，即n的全排列，要求所产生的任一数字序列中不允许出现重复的数字。

输入

输入 n(1≤n≤9)

输出

由1～n组成的所有不重复的数字序列，每行一个序列。每个数字占5列。

样例输入

4

样例输出

    1    2    3    4
    1    2    4    3
    1    3    2    4
    1    3    4    2
    1    4    2    3
    1    4    3    2
    2    1    3    4
    2    1    4    3
    2    3    1    4
    2    3    4    1
    2    4    1    3
    2    4    3   1 
    3    1    2    4
    3    1    4    2
    3    2    1    4
    3    2    4    1
    3    4    1    2
    3    4    2    1
    4    1    2    3
    4    1    3    2
    4    2    1    3
    4    2    3    1
    4    3    1    2
    4    3    2    1

代码：


#include <iostream>
using namespace std;
int n, m;
int a[15] = {0};
int b[15];
void dfs(int i)
{
    if (n == i)              //搜至终点输出答案
    {
        for (int j = 0; j < n; j++)
            printf("%5d", a[j]);
        printf("\n");
    }
    else
        for (int j = 1; j <= n; j++)
            if (b[j] == 0)   //当前位置没被用过
            {
                b[j] = 1;    //标记为用过
                a[i] = j;    //存答案
                dfs(i + 1);  //深入下一个位置
                b[j] = 0;    //回溯
            }  
}
 
int main()
{
    cin >>n;
    dfs(0);                
}

问题 B: 排列棋子

题目描述

将M个白棋子与N个黑棋子排成一行，可以排成多种不同的图案。例如：2个白棋子和2个黑棋子，一共可以排成如下图所示的6种图案（根据组合数计算公式：

请你编写一段程序，输出M个白棋子与N个黑棋子能够组成的所有图案。

为了避免程序输出结果过多导致严重超时，特别限制：1≤M,N≤6

输入

两个正整数M,N表示白棋子与黑棋子的数量，并且满足1≤M,N≤6

输出

M个白棋子与N个黑棋子可以排列的所有图案。
要求：每行输出一种图案，白棋子用0表示，黑棋子用1表示，按升序输出

样例输入

【测试样例1】
2 1
【测试样例2】
2 2
【测试样例3】
2 3

样例输出

代码1：用next_permutation()函数自动去重


#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
int main(){
    int n,m;
    cin >> m>>n;
    int a[10];
	for (int i = 1; i <= m;i++)
	{
		a[i] = 0;
	}
	for (int i = m+1; i <= m+n+1;i++)
	{
		a[i] = 1;
	}
	do{
        for (int i = 1; i <= m+n;i++){
            printf("%d", a[i]);
        }
        cout << endl;
    } while (next_permutation(a+1,a+n+m+1));
    return 0;
}

代码2：


#include <iostream>
int usedArr[13], res[13], m, n,flag = 1;
int chess[13];
using namespace std;
void permute(int k) {
    if (k == m + n + 1) {
        for (int i = 1; i <=  m+n; i++)
            printf("%d",res[i]);
        puts("");
        flag = 0;
        return;
    }
    for (int i = 1; i <= m+n; i++) {
        if (!usedArr[i] && (res[k] != chess[i] || flag) ) {
        	flag = 1;
        	usedArr[i] = 1; // //判断是否用过
            res[k] = chess[i];
            permute(k + 1); 
            usedArr[i] = 0;
        }
    }
}
int main() {
	// M个白棋子与N个黑棋子
    cin >> m >> n;
    for (int i = 1; i <= m; i++)
        chess[i] = 0;
    for (int i=m+1; i <= m + n; i++)
        chess[i] = 1;
    permute(1);
    return 0;
}

问题 C: 组合的输

题目描述

排列与组合是常用的数学方法，其中组合就是从n个元素中抽出r个元素(不分顺序且r<＝n)，我们可以简单地将n个元素理解为自然数1，2，…，n，从中任取r个数。

现要求你用递归的方法输出所有组合。

例如n＝5，r＝3，所有组合为：

l 2 3 l 2 4 1 2 5 l 3 4 l 3 5 1 4 5 2 3 4 2 3 5 2 4 5 3 4 5

输入

一行两个自然数n、r(1<n<21，1<＝r<＝n)。

输出

所有的组合，每一个组合占一行且其中的元素按由小到大的顺序排列，每个元素占三个字符的位置，所有的组合也按字典顺序。

样例输入

5 3

样例输出

代码：


#include<iostream>
#include<cstdio>
using namespace std;
int a[30];
// bool v[30] = {false};                 //不需要visit数组，本来就是升序状态
int n,r,u;
void dfs(int i,int u){
    if(i==r){
        for (int j = 0; j < r;j++){
            printf("%3d", a[j]);
        }
        cout << endl;
    }
    for (int j = u+1; j <= n;j++){        //前面的数必须比后面的数小
            a[i] = j;
            dfs(i + 1,j);
    }
}
 
int main(){
    cin >> n>>r;
    dfs(0,0);
}

问题 D: 有重复元素的排列问题

题目描述

设R={ r1, r2 , …, rn}是要进行排列的n个小写字母。其中小写字母r1, r2 , …, rn可能相同。试设计一个算法，列出R的所有不同排列。

给定n 以及待排列的n 个小写字母。计算出这n 个小写字母的所有不同排列。

输入

输入数据的第1 行是小写字母个数n，1≤n≤500。接下来的1 行是待排列的n个元素。

输出

计算出的n个小写字母的所有不同排列并按字典序输出。文件最后1行中的数是排列总数。

样例输入

4
aacc

样例输出

aacc
acac
acca
caac
caca
ccaa
6

代码：


#include<iostream>
#include<cstdio>
using namespace std;
char ans[501];
int v[128];         //用字母出现的次数作为标记
int n,cnt=0;
void dfs(int i){
    if(i==n){
        for (int j = 0; j < n;j++){
            printf("%c", ans[j]);
        }
        cout << endl;
        cnt++;
    }
    for (char j ='a'; j <= 'z';j++){     //遍历每一个字母，通过字母数量保存答案
        if(v[j]>0){                      //判断是否有字母
            ans[i] = j;
            v[j] --;                     //j位置的字母被使用，数量-1
            dfs(i + 1);
            v[j] ++;                     //回溯
        }
    }
}
 
int main(){
    string s;
    cin >> n >> s;
    for (int i = 0; i < s.size();i++){   
        v[s[i]]++;                        //保存字母出现次数
    }
    dfs(0);
    cout << cnt;
    return 0;
}

问题 E: 部分排列

题目描述

从4个字母ABCD中取出2个不同的字母，可以得到的排列共有12种：AB、AC、AD、BA、BC、BD、CA、CB、CD、DA、DB、DC

如果有ABCD...n个不同的字母，从中取出m个不同的字母，可以得到哪些排列？

输入

正整数n,m（满足m≤n≤9）

输出

Pnm个不同的排列，每行一个

样例输入

4 3

样例输出

ABC
ABD
ACB
ACD
ADB
ADC
BAC
BAD
BCA
BCD
BDA
BDC
CAB
CAD
CBA
CBD
CDA
CDB
DAB
DAC
DBA
DBC
DCA
DCB

代码：


#include<iostream>
#include<cstdio>
using namespace std;
char a[30];
bool v[30] = {false};
int n,r,u;
void dfs(int i,int u){
    if(i==r){
        for (int j = 0; j < r;j++){
            printf("%c", a[j]);
        }
        cout << endl;
    }
    for (int j = 0; j <n;j++){
        if(v[j]!=true){
            a[i] = j+'A';
            v[j] = true;
            dfs(i + 1,j);
            v[j] = false;
        }
    }
}
 
int main(){
    cin >> n>>r;
    dfs(0,0);
}

参考原贴：回溯算法总结_Ramelon的博客-CSDN博客

问题 A: N皇后问题(Queen.cpp)

题目描述

在N*N的棋盘上放置N个皇后（n<=10）而彼此不受攻击（即在棋盘的任一行，任一列和任一对角线上不能放置2个皇后），编程求解所有的摆放方法。

输入

输入：n

输出

每行输出一种方案，每种方案顺序输出皇后所在的列号，每个数占5列。若无方案，则输出no solute!

样例输入

4

样例输出

2 4 1 3

3 1 4 2

题意：给定n个皇后，如何放置这n个皇后使其相互之间不会被攻击，输出放置的方案

思路：

由于皇后的位置受到上述三条规则约束，我们必须通过一些技术手段来判断当前皇后的位置是否合法。

1.皇后的编号从 0 ~ N - 1 （N表示皇后的数量），这样编号的想法很简单：数组下标从0开始（这样方便后续对其位置的说明）。

2.使用一维数组 putInf 对每一行皇后的存放位置进行保存，因此得到解向量 (putInf[0], putInf[1], putInf[3], … , putInf[N - 1])，putInf[i] 表示第 i 个皇后被放置到了第 putInf[i] + 1 列上（putInf数组中存储的是列号，范围为 0 ~ N - 1）;

3.第二个条件：各皇后不同列， N 皇后放在 N x N 的棋盘上，那么每一列最多且必须放置一个皇后，这里我用了一个 used数组对每一列的摆放情况进行记录， used[i] = true 表示第 i 列已经放置了皇后，used[i] = false 表示第i列暂未放置皇后，这样我们可以保证不在一列上放置多个皇后，也就能满足各皇后不同列的规则。

4.各皇后不能处于同一对角线位置：假设两皇后位置坐标分别为(i, j) 、（l, k），那么根据直线斜率公式：

(i - l) / (j - k) = 1 求解得 i - l == j - k ①
(i - l) / (j - k) = -1 求解得 i - l == k - j ②
这两种情况出现时表明处于同一对角线，那么要满足摆放规则就必须满足
| i - l | != | j - k | （“| |” 表示绝对值）

参考原文链接：https://blog.csdn.net/Genius_bin/article/details/116105020

代码：


#include<iostream>
#include<vector>
#include<iomanip>
using namespace std;
vector<bool> used(15, false);  //每列只能有一个皇后，记录每一列的状态
vector<int> x;         //每一行皇后的放置情况
bool limit = false;
int n, cur=0;
bool check(int cur,int lie){    //判断cur行的lie列放置对的皇后是否合法
    for (int i = cur -1; i >=0;i--){
        //我们的解空间树已经去除一行一列置放相同元素
		//（每一个皇后被放在不同行以及不同列）的情况
		//因此我们只需要判断皇后是否成斜线即可
        if(cur-i==abs(lie-x[i]))
        //当前位置与之前的皇后处于同一斜线上
            return false;
    }
    return true;
}
void quee(int cur){
    if(cur>=n){     //n个皇后放置完毕
        limit = true;
        for (vector<int>::iterator it = x.begin(); it != x.end();it++){
            cout << setw(5) << *it+1;
        }
        cout << endl;
        return;
    }
    //i : 当前行皇后准备放的列数
    for (int i = 0; i < n;i++){    //cur行i列的位置
        if(used[i])
            continue;          //位置被使用过，跳过
        if(check(cur,i)){
            //当前位置置放与之前不冲突 将皇后加入
            x.push_back(i);
            used[i] = true;
            quee(cur + 1);
            used[i] = false;     //回溯
            x.pop_back();
        }
    }
}
int main(){
    cin >> n;;
    quee(0);
    if(!limit)
        cout << "no solute!";
    return 0;
}

B - N皇后问题

在N*N的方格棋盘放置了N个皇后，使得它们不相互攻击（即任意2个皇后不允许处在同一排，同一列，也不允许处在与棋盘边框成45角的斜线上。
你的任务是，对于给定的N，求出有多少种合法的放置方法。

Input

共有若干行，每行一个正整数N≤10，表示棋盘和皇后的数量；如果N=0，表示结束。

Output

共有若干行，每行一个正整数，表示对应输入行的皇后的不同放置数量。

Sample

Inputcopy	Outputcopy
1 8 5 0	1 92 10

同样是n皇后问题，只不过输出的是有多少种放置方法

只需要在找到答案时sum+1

tips：直接搜索会超时，先打表把n<=10的答案存在一个数组里，输出ans[n]

问题 B: 拆分自然数

题目描述

任何一个大于1的自然数n(n <= 10)，总可以拆分成若干个小于n的自然数之和。

当n=7共14种拆分方法：

7=1+1+1+1+1+1+1

7=1+1+1+1+1+2

7=1+1+1+1+3

7=1+1+1+2+2

7=1+1+1+4

7=1+1+2+3

7=1+1+5

7=1+2+2+2

7=1+2+4

7=1+3+3

7=1+6

7=2+2+3

7=2+5

7=3+4

输入

输入自然数n

输出

输出拆分的方案。

样例输入

7

样例输出

1+1+1+1+1+1+1
1+1+1+1+1+2
1+1+1+1+3
1+1+1+2+2
1+1+1+4
1+1+2+3
1+1+5
1+2+2+2
1+2+4
1+3+3
1+6
2+2+3
2+5
3+4

题意：将n拆分，重复的不输出如：7=1+6和7=6+1

思路：dfs传入最小数1，然后逐步回溯放大最后一位数字


#include<iostream>
#include<vector>
using namespace std;
int n;
vector<int> ans;
vector<int>::iterator it = ans.begin();
void dfs(int temp,int sum){
    if(sum==n){                 //找到答案输出
        cout << ans[0];
        for (int i = 1; i < ans.size();i++){
            cout << "+" << ans[i];  
        }
        cout << endl;
    }
    for (int i = temp; i < n;i++){      //从所有数都是1开始搜索
        if((sum+i)<=n){                 //sum是递增的，直到sum+i=n
            ans.push_back(i);
            dfs(i, sum+i);              
            ans.pop_back();             //回溯
        }
    }
}
 
int main(){
    cin >> n;
    dfs(1, 0);
}

问题 D: 4连通迷宫

题目描述

给定一个M*M(2≤M≤9)的迷宫，迷宫用0表示通路，1表示围墙。

迷宫的入口和出口分别位于左上角和右上角，入口和出口显然都是0。

在迷宫中移动可以沿着上、下、左、右四个方向进行，前进格子中数字为0时表示可以通过，为1时表示围墙不可通过，需要另外再找找路径。

请统计入口到出口的所有路径（不重复），并输出路径总数。若从入口无法到达出口，请输出0。

输入

第一行输入1个正整数M(≤M≤9)，表示迷宫是M行M列。

第2行到第n+1行是一个M阶的0-1方阵。

输出

统计入口到出口的所有路径（不重复），并输出路径总数。若从入口无法到达出口，请输出0。

样例输入

样例输出

1

题意：计算走出迷宫的路数

思路：dfs找终点，每找到一次终点sum+1


#include<iostream>
#include<cstring>
using namespace std;
int n, m,qx,qy,sum=0;
int visit[21][21];  //检查数组
int a[21][21];
int dx[] = {0, 1, 0, -1}; //方向数组x
int dy[] = {1, 0, -1, 0}; //方向数组y
 
void dfs(int x,int y){
    if(x==0&&y==n-1){     //走到终点，路数+1；
        sum++;       
        return;
    }
    else{
        visit[x][y] = 1;  //当前位置记为走过
        for (int i = 0; i < 4;i++){   //枚举四个方向
            //下一个位置的坐标
            int nx = x + dx[i];
            int ny = y + dy[i];
            //判断是否到边界，下个位置是否可走
            if (nx >= 0 && nx < n && ny >= 0 && ny < n && visit[nx][ny] != 1&&a[nx][ny]!=1){
                dfs(nx, ny);     //进入下一个位置
                visit[nx][ny] = 0;   //回溯，上一个位置恢复成没走过
            }
        }
    }
}
 
int main(){
    cin >> n;
    for (int i = 0; i < n;i++){
        for (int j = 0; j < n;j++){
            cin >> a[i][j];
        }
    }
    dfs(0, 0);
    cout << sum << endl;
    return 0;
}

问题 A: Red and Black

题目描述

一个矩形的房间铺着红色或者黑色的方砖。一个人站在红砖上不能移动，在黑砖上可以沿着上、下、左、右4个方向移动到相邻的方砖。请编写一个程序，计算从起点出发可以到达的黑色方砖的数量（包括起点在内）。

起点是@，要求：遍历所有黑砖。

输入

输入第一行是两个正整数W和H； W和H分别表示x方向和y方向上的方砖数量。W和H都是正整数并且不超过20.

接下来有H行，每行包含W个字符。每个字符表示方砖的颜色如下。

'.' - 黑砖

'＃' - 红砖

'@' - 起点

输出

输出从起点出发可以到达的黑砖的数量（包括起点在内）。

样例输入

5 4
....#
.....
#@...
.#..#

样例输出

15

题意：计算可到达区域中 '.' 的数量

思路1：dfs 一条路走到底，直至无路可走，类似上一题迷宫


#include<iostream>
#include<cstring>
using namespace std;
int n, m,qx,qy,sum=0;
int visit[21][21];  //检查数组
char a[21][21];
int dx[] = {0, 1, 0, -1}; //方向数组x
int dy[] = {1, 0, -1, 0}; //方向数组y
 
void dfs(int x,int y){
 
    sum++;              //每往前一步就+1
    visit[x][y] = 1;    //走过的位置标记为1
 
    for (int i = 0; i < 4;i++){   //四个方向
        int nx = x + dx[i];       //下一步进入的新坐标
        int ny = y + dy[i];
 
        //判断下一个位置是否能继续走，即nx,ny是否到边界，是否走过
        if(nx>=0&&nx<n&&ny>=0&&ny<m&&visit[nx][ny]!=1&&a[nx][ny]=='.') 
            dfs(nx, ny);
    }
}
 
int main(){
    while(cin>>m>>n){
        if(n==0&&m==0)
            break;
        sum = 0;
        memset(visit, 0, sizeof(visit));   //清零检查数组
        for (int i = 0; i < n;i++){
            for (int j = 0; j < m;j++){
                cin >> a[i][j];
                if(a[i][j]=='@'){          //遇到@标记起点
                    qx = i;
                    qy = j;
                }
            }
        }
        dfs(qx, qy);            //从起点开始搜索
        cout << sum<<endl;
    }
    return 0;
}

思路2：bfs搜索所有可到达区域，直到所有位置都到过


#include<bits/stdc++.h>
using namespace std;
int W,H,num,dx,dy;
char room[25][25];
#define CHECK(x,y)(x<W&&x>=0&&y<H&&y>=0)
typedef struct{
    int x,y;
}Node;//代表x，y坐标
int dir[4][2]={
    {-1,0},{0,-1},{1,0},{0,1}
};
void bfs(){
    Node start,next;
    start.x=dx,start.y=dy;
    queue<Node>q;
    q.push(start);
    while(!q.empty()){
        start=q.front();
        q.pop();
        for(int i=0;i<4;i++){
            next.x=start.x+dir[i][0];
            next.y=start.y+dir[i][1];
            if(CHECK(next.x,next.y)&&room[next.x][next.y]=='.'){
                num++;
                room[next.x][next.y]='#';
                q.push(next);
            }
        }
    }
}
int main(){
    int x,y;
    while(~scanf("%d%d",&W,&H)){
        if(!W&&!H)break;
        for(y=0;y<H;y++){
            for(x=0;x<W;x++){
                cin>>room[x][y];
                if(room[x][y]=='@')dx=x,dy=y;
            }
        }
        num=1;
        bfs();
        printf("%d\n",num);
    }
}

问题 B: 细胞有几个

题目描述

一矩形阵列由数字0到9组成,数字1到9代表细胞,细胞的定义为沿细胞数字上下左右还是细胞数字则为同一细胞,求给定矩形阵列的细胞个数。

如: 阵列 4 10

0234500067

1034560500

2045600671

0000000089

有4个细胞。

输入

输入有多行，第一行表示矩阵阵列的行数m和列数n（m<=70，n<=70）；

接下来的m行n列为0-9等10个数字构成的矩阵。

输出

输出细胞个数。

样例输入

样例输出

4

题意：给定m*n的矩阵，计算细胞数量，上下左右由非0数字相连接的模块记为1 个细胞

思路：在循环中bfs，遍历矩阵，遇到非0数字就开始bfs，走过的位置都归零，直至无路可走，则细胞数量+1，继续遍历矩阵

代码：


#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
 
struct point{         //坐标结构体
	int x, y;
};
 
int dx[] = {-1,0,1,0};
int dy[] = {0,1,0,-1};   //坐标数组
 
char mp[71][71];     //地图
point s;	 //起点
queue<point> q;				//队列放邻接坐标
int m,n,ans = 0;
 
bool check(point t){
    if(t.x>=0&&t.x<m&&t.y>=0&&t.y<n&&mp[t.x][t.y]!='0'){
        return true;
    }
    return false;
}
 
void bfs(int x,int y){
    ans++;
    s.x = x, s.y = y;
    q.push(s);
    mp[x][y] = 0;
    while (!q.empty()){
        point p=q.front();
        q.pop();
        for (int i = 0; i < 4;i++){
            point np;
            np.x = p.x + dx[i];
            np.y = p.y + dy[i];
            if(check(np)){
                q.push(np);
                mp[np.x][np.y] = '0';
            }
        }
    }
}
 
int main(){
    cin >> m >> n;
    for (int i = 0; i < m;i++){
        for (int j = 0; j < n;j++){
            cin >> mp[i][j];
        }
    }
    for (int i = 0; i < m;i++){
        for (int j = 0; j < n;j++){
            if(mp[i][j]!='0')
                bfs(i, j);
        }
    }
    cout << ans << endl;
}

问题 C: 最少转弯问题

题目描述

给出一张地图，这张地图被分为n×m（n,m<=100）个方块，任何一个方块不是平地就是高山。平地可以通过，高山则不能。现在你处在地图的（x1,y1）这块平地，问：你至少需要拐几个弯才能到达目的地（x2,y2）？你只能沿着水平和垂直方向的平地上行进，拐弯次数就等于行进方向的改变（从水平到垂直或从垂直到水平）的次数。例如：如图，最少的拐弯次数为5。

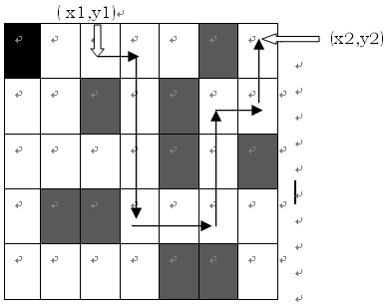
输入

第1行：n m

第2至n+1行：整个地图地形描述（0：空地；1：高山），

如（图）第2行地形描述为：1 0 0 0 0 1 0

第3行地形描述为：0 0 1 0 1 0 0

……

第n+2行：x1 y1 x2 y2 （分别为起点、终点坐标）

输出

输出s （即最少的拐弯次数）

样例输入

5 7
1 0 0 0 0 1 0 
0 0 1 0 1 0 0 
0 0 0 0 1 0 1 
0 1 1 0 0 0 0 
0 0 0 0 1 1 0
1 3 1 7

样例输出

5

题意：找最小转弯次数


#include<iostream>
#include<queue>
using namespace std;
const int N = 105;
const int dx[] = {-1, 0, 1, 0},
		  dy[] = { 0, 1, 0,-1};
int n,m,x1,y1,x2,y2;
bool g[N][N];
struct node{
	int x,y,turn;
	node(){ }
	node(int a,int b,int c):x(a),y(b),turn(c){ }
};
queue<node> q;
 
int bfs(){
	q.push(node(x1,y1,0));
	g[x1][y1] = true;
	while (!q.empty()){
		node k=q.front(); q.pop();
		if (k.x==x2 && k.y==y2) return k.turn-1;	//到达终点 队头-1为答案
		for (int i=0; i<4; i++){	//四个方向
			int x=k.x+dx[i],y=k.y+dy[i];
			while (x>=1 && x<=n && y>=1 && y<=m && !g[x][y]){
				q.push(node(x,y,k.turn+1));
				g[x][y] = true;
				x+=dx[i]; y+=dy[i];		//沿着这个方向一直走下去
			}
		}
	}
}
 
int main(){
	cin>>n>>m;
	for (int i=1; i<=n; i++)
		for (int j=1; j<=m; j++) cin>>g[i][j];
	cin>>x1>>y1>>x2>>y2;
	if (x1==x2 && y1==y2) cout<<0<<endl;
	else cout<<bfs()<<endl;
	return 0;
}

问题 D: 马的移动

题目描述

小明很喜欢下国际象棋，一天，他拿着国际象棋中的“马”时突然想到一个问题：

给定两个棋盘上的方格A和B，马从A跳到B最少需要多少步？现请你编程解决这个问题。

提示：国际象棋棋盘为8格*8格，马的走子规则为，每步棋先横走或直走一格，然后再往外斜走一格。

输入

输入包含多组测试数据。

每组输入由两个方格组成，每个方格包含一个小写字母（a~h），表示棋盘的列号，和一个整数（1~8），表示棋盘的行号。

输出

对于每组输入，输出一行“To get from xx to yy takes n knight moves.”。

样例输入

e2 e4
a1 b2
b2 c3
a1 h8
a1 h7
h8 a1
b1 c3
f6 f6

样例输出

To get from e2 to e4 takes 2 knight moves.
To get from a1 to b2 takes 4 knight moves.
To get from b2 to c3 takes 2 knight moves.
To get from a1 to h8 takes 6 knight moves.
To get from a1 to h7 takes 5 knight moves.
To get from h8 to a1 takes 6 knight moves.
To get from b1 to c3 takes 1 knight moves.
To get from f6 to f6 takes 0 knight moves.

题意：算出起点到终点需要的步数，移动必须按照马的行动规则

思路：用两个数组记录马行动的八个方向然后bfs，point结构体中存放xy坐标和步数depth，每走一步depth+1

代码：


#include<iostream>
#include<queue>
#include<cstdio>
#include<cstring>
#include<map>
using namespace std;
 
struct point{         //坐标结构体
	point(int a, int b,int d) { x = a;y = b;depth = d;}   //重载坐标函数
	int isvalid() { return x >= 1 && x <= 8 && y >= 1 && y <= 8; }   //重载自定义是否超出棋盘范围
	int x, y,depth;
};
 
int dx[] = {-1, -2, 1, 2, 1, 2, -1, -2};
int dy[] = {-2, -1, -2, -1, 2, 1, 2, 1};   //坐标数组
 
int board[10][10] = {0};     //棋盘
point s(0,0,0), t(0,0,0);	 //起点，终点
queue<point> q;				//队列
 
int main(){
	char x1, x2;
	int y1, y2;
	while(~scanf("%c%d %c%d",&x1,&y1,&x2,&y2)){
		memset(board, 0, sizeof(board));         //重置棋盘
		s.x = x1 - 'a' + 1;s.y = y1;
		t.x = x2 - 'a' + 1;t.y = y2;
 
		if(x1==x2&&y1==y2){				//起点终点在同一个点单独判断
				printf("To get from %c%d to %c%d takes 0 knight moves.\n", x1, y1, x2,y2);
				continue;
		}
		q.push(s);                     //把起点放进队列 
		while(!q.empty()){             
			point p = q.front();       //取出队列头元素
			q.pop();                   //弹出
 
			if(!p.isvalid()) continue; //超出边界就跳过 
			if(board[p.x][p.y]!=0) continue;  //走过该点跳过
			board[p.x][p.y] =p.depth;     //把走过的位置更新为步数
 
			if(p.x==t.x&&p.y==t.y){        //走到终点
				printf("To get from %c%d to %c%d takes %d knight moves.\n", x1, y1, x2, y2, p.depth);
			}
			for (int i = 0; i < 8;i++){    //往八个方向深入
				q.push(point(p.x + dx[i], p.y + dy[i],p.depth+1));
			}
		}
	}
}

B - Catch That Cow

Farmer John has been informed of the location of a fugitive cow and wants to catch her immediately. He starts at a point N (0 ≤ N ≤ 100,000) on a number line and the cow is at a point K (0 ≤ K ≤ 100,000) on the same number line. Farmer John has two modes of transportation: walking and teleporting.

* Walking: FJ can move from any point X to the points X - 1 or X + 1 in a single minute
* Teleporting: FJ can move from any point X to the point 2 × X in a single minute.

If the cow, unaware of its pursuit, does not move at all, how long does it take for Farmer John to retrieve it?

Input

Line 1: Two space-separated integers: N and K

Output

Line 1: The least amount of time, in minutes, it takes for Farmer John to catch the fugitive cow.

Sample

Inputcopy	Outputcopy
5 17	4

Hint

The fastest way for Farmer John to reach the fugitive cow is to move along the following path: 5-10-9-18-17, which takes 4 minutes.

题意：算出农夫找到牛需要的时间，农夫的位置为x，移动规则，x+1,x-1或者传送到x*2的位置，花的时间都是一分钟，牛的位置不会变

思路：其实与马的移动类似，而且是在一维的轴上移动

代码：


#include<iostream>
#include<queue>
#include<cstring>
using namespace std;
 
struct point{              //坐标点，step保存步数
    int x, step;
};
int mp[100001]={0};       //坐标轴
int n, m,ans=0;
point s, z;               //起点终点
queue<point> q;
 
void bfs(){
    s.step = 0;            //步数初始化为0
    q.push(s);
    mp[s.x] = 1;
    while(!q.empty()){
        point p = q.front();
        q.pop();
        if(p.x==z.x){       //找到终点输出步数
            cout << p.step;
            return;
        }
        for (int i = 0; i < 3;i++){      //三种方向
            point nx;
            if(i==0)
                nx.x= p.x - 1;
            if(i==1)
                nx.x= p.x + 1;
            if(i==2)
                nx.x= p.x *2;
            if(nx.x>=0&&nx.x<=100000&&mp[nx.x]==0){
                mp[nx.x] = 1;                 //更新位置状态
                nx.step = p.step + 1;         //更新步数
                q.push(nx);                 //一定要放在更新后！！
            }
        }
    }
}
 
int main(){
    cin >> s.x>> z.x;
    bfs();
}

C - Find The Multiole

Given a positive integer n, write a program to find out a nonzero multiple m of n whose decimal representation contains only the digits 0 and 1. You may assume that n is not greater than 200 and there is a corresponding m containing no more than 100 decimal digits.

Input

The input file may contain multiple test cases. Each line contains a value of n (1 <= n <= 200). A line containing a zero terminates the input.

Output

For each value of n in the input print a line containing the corresponding value of m. The decimal representation of m must not contain more than 100 digits. If there are multiple solutions for a given value of n, any one of them is acceptable.

Sample

Inputcopy	Outputcopy
2 6 19 0	10 100100100100100100 111111111111111111

题意：输入整数n,找出只能由0和1组成且能整除n的数字

思路：搜索方向是 x*10 或者 x*10+1

虽然是在bfs的题库但是用bfs代码提交会内存超限，所以得用dfs做

bfs代码：


#include<iostream>
#include<queue>
using namespace std;
queue<long long> q;
long long bfs(int n)
{
	long long start = 1;
	q.push(start);
	while (!q.empty()) {
		start = q.front();
		q.pop();
		if (start % n == 0) {
			return start;
		}
		q.push(start * 10);
		q.push(start * 10 + 1);
	}
}
int main()
{
	int n;
	while (cin >> n && n) {
		while (!q.empty()) {
			q.pop();
		}
		cout << bfs(n) << endl;
	}
}

dfs代码：


#include<cstdio>
#include<iostream>
#include<cstring>
using namespace std;
typedef long long ll;
int n, flag;
 
void dfs(ll x, int k){
    if(flag || k>=19)   return ;
 
    if(x%n==0){
        flag=1;
        cout<<x<<endl;
        return ;
    }
    dfs(x*10, k+1);
    dfs(x*10+1, k+1);
    return  ;
}
 
int main(){
    while(cin>>n && n){
        flag=0;
        dfs(1,0);
    }
    return 0;
}

贪心类

问题 B: 分牌

题目描述

有 N 堆纸牌，编号分别为 1，2，…, N。每堆上有若干张，但纸牌总数必为 N 的倍数。可以在任一堆上取若干张纸牌，然后移动。

移牌规则为：在编号为 1 堆上取的纸牌，只能移到编号为 2 的堆上；在编号为 N 的堆上取的纸牌，只能移到编号为 N-1 的堆上；其他堆上取的纸牌，可以移到相邻左边或右边的堆上。

现在要求找出一种移动方法，用最少的移动次数使每堆上纸牌数都一样多。

例如 N=4，4 堆纸牌数分别为： ①　9　②　8　③　17　④　6

移动3次可达到目的：

从 ③ 取4张牌放到④（9 8 13 10）->从③取3张牌放到 ②（9 11 10 10）-> 从②取1张牌放到①（10 10 10 10）。

输入

N（N 堆纸牌，1 <= N <= 100）

A1 A2 … An （N 堆纸牌，每堆纸牌初始数，l<= Ai <=10000）

输出

所有堆均达到相等时的最少移动次数。

样例输入

4

9 8 17 6

样例输出

3

题意：计算将n堆牌均需要的步数

思路：

按照从左到右的顺序移动纸牌。如第I堆的纸牌数不等于平均值，则移动一次（即ans加1），分两种情况移动：

1．若a[i]>average，则将a[i]-average张从第I堆移动到第I+1堆；

2．若a[i]<average，则将average-a[i]张从第I+1堆移动到第I堆。

代码：


#include<bits/stdc++.h>
using namespace std;
int a[105];
int main(){
    int n;
    cin >> n ;
    int ans = 0, sum = 0;
    for (int i = 1.; i <= n;i++){
        cin >> a[i];
        sum += a[i];
    }
    int average = sum / n;
    for (int i = 1; i < n;i++){
        if(a[i]>average){
            int c = a[i] - average;
            a[i + 1] +=c;
            ans++;
        }
        if(a[i]==average)
            continue;
        if(a[i]<average){
            int c = average - a[i];
            a[i+1] -= c;
            ans++;
        }
    }
    cout << ans;
}

问题 C: 删数问题

题目描述

输入一个高精度的正整数N，去掉其中任意S个数字后剩下的数字按原左右次序组成一个新的正整数。编程对给定的N和S，寻找一种方案使得剩下的数字组成的新数最小。

输出新的正整数。（N不超过240位）输入数据均不需判错。

输入

n
s

输出

最后剩下的最小数。

样例输入

175438

样例输出

13

题意：删除s个数使得n最小

思路：字符串的方式读入N,每次判断找出n中单调增加区域最大的数字删掉，最后的结果要去除前导0

代码：


#include<bits/stdc++.h>
using namespace std;
int main(){
    string a;
    int n;
    cin >> a>>n;
    while(n!=0){
        int i = 0;
        while(a[i]<=a[i+1]){
            i++;
        }
        a.erase(i, 1);
        n--;
    }
    int i;
    for (i = 0; i < a.size();i++){
        if(a[i]!='0')
            break;
    }
    for (int j = i; j < a.size();j++){
        cout << a[j];
    }
    return 0;
}

问题 D: 活动选择

题目描述

学校在最近几天有n个活动，这些活动都需要使用学校的大礼堂，在同一时间，礼堂只能被一个活动使。由于有些活动时间上有冲突，学校办公室人员只好让一些活动放弃使用礼堂而使用其他教室。　　

现在给出n个活动使用礼堂的起始时间bi和结束时间ei(bi < ei<=32767)，请你帮助办公室人员安排一些活动来使用礼堂，要求安排的活动尽量多。

输入

第一行一个整数n(n<=1000)；接下来的n行，每行两个整数，第一个bi，第二个是ei(bi < ei<=32767)

输出

输出最多能安排的活动个数

样例输入

样例输出

4

题意：算出做多可以安排的活动数

思路： 可以先对结束时间进行排序（开始时间相对应一起），那么第一个肯定就是最早结束的活动即f1最小，那么就要排除与f1时间相重复的s1都应排除（不可选），而要找si>=f1的活动开始时间（因为已经排过序了就直接遍历往后找第一个符合的就行）。以此类推，处理完所有活动时间。


#include<bits/stdc++.h>
using namespace std;
struct node{
    int l, r;
};
bool cmp(node a,node b){
    if(a.r==b.r)
        return a.l > b.l;
    return a.r < b.r;
}
int main(){
    node a[1001];
    int n;
    cin >> n;
    for (int i = 0; i < n;i++){
        cin >> a[i].l>>a[i].r;
    }
    sort(a, a+n, cmp);
    int mr = a[0].r;
    int ans = 1;
    for (int i = 1; i < n;i++){
        if(a[i].l>=mr){
            mr = a[i].r;
            ans++;
        }
    }
    cout << ans;
    return 0;
}

问题 E: 最大整数

题目描述

设有n个正整数（n≤20），将它们联接成一排，组成一个最大的多位整数。例如：n=3时，3个整数13，312，343联接成的最大整数为：34331213 又如：n=4时，4个整数7，13，4，246联接成的最大整数为：7424613

输入

输入格式如下：第一行为正整数n，第2行为n个正整数，2个正整数之间用空格间隔。

输出

输出n个数连接起来的最大整数

样例输入

3

13 312 343

样例输出

34331213

题意：将n个整数组合成一个整数，且为可组合中最大的

思路: 如果a+b>b+a且a在b后面就交换a,b的位置


#include<bits/stdc++.h>
using namespace std;
int main(){
    vector<string>a;
    string s,x;
    int n;
    cin >> n;
    for (int i = 0; i < n;i++){
        cin >> s;
        a.push_back(s);
    }
    for (int i = 0; i < a.size();i++){
        for (int j = i; j < a.size();j++){
            if((a[i]+a[j])>(a[j]+a[i])) continue;
            else{
                swap(a[i], a[j]);
            }
        }
    }
    for (int i = 0; i < n;i++){
        cout << a[i];
    }
        return 0;
}

D - Strange fuction

Now, here is a fuction:
F(x) = 6 * x^7+8*x^6+7*x^3+5*x^2-y*x (0 <= x <=100)
Can you find the minimum value when x is between 0 and 100.

Input

The first line of the input contains an integer T(1<=T<=100) which means the number of test cases. Then T lines follow, each line has only one real numbers Y.(0 < Y <1e10)

Output

Just the minimum value (accurate up to 4 decimal places),when x is between 0 and 100.

题意：求F(x) [0,100]之间的极小值

思路：求函数极值点转化为求导函数0点，用实数二分的方法求0点


#include <cmath>
#include <cstdio>
#include <iostream>
using namespace std;
const double esp=1e-6;
 
double F(double x,double y){         //原函数
    return 6*pow(x,7)+8*pow(x,6)+7*pow(x,3)+5*pow(x,2)-y*x;
}
double f(double x,double y){         //导数
    return 42*pow(x,6)+48*pow(x,5)+21*pow(x,2)+10*pow(x,1)-y;
}
int main(){
    int n;
    cin >> n;
    while(n--){
        double t,mid,l,r;
        cin >> t;
        l = 0.0, r = 100.0;
        while(r-l>esp){             //二分求零点
            mid = (l + r) /2;
            if(f(mid,t)>0){
                r = mid;
            }
            else{
                l = mid;
            }
        }
        printf("%.4f\n", F(mid, t));   //把0点带入原函数
    }
    return 0;
}

分治类

问题 D: 解方程

题目描述

求方程f(x)=2^x+3^x-4^x=0在[1，2]内的根。

输入

输入m(0<=m<=8)，控制输出精度

输出

printf("%.*lf",m,l);  //m为小数点后精度范围

输出方程f(x)=0的根，x的值精确小数点m位

样例输入

3

样例输出

1.507

提示：2^x可以表示成exp(x*ln(2))的形式。

题意：输入给定整数作为精度范围，计算出 f(x) 在[1,2]的根

思路：实数二分求0点，精度范围1e-9,还有一个难点在于根据输入的数字来控制输出的精度，并且要四舍五入

根据输入的数字控制输出的精度

printf("%.*lf",m,l);   //m为小数点后的精度范围

代码：


#include<iostream>
#include<cmath>
using namespace std;
 
//方程的解
bool  check(double x){
    double y = pow(2, x) + pow(3, x) - pow(4, x);
    return y >= 0;
}
int main(){
    int m;
    cin>>m;
    // cout<<1e(2*m)<<endl;
    //[l,r]进行二分求解
    double l = 1, r = 2;
    while((r-l)>=1e-9){      //精度范围内
        double mid = (r + l) / 2;  //[l,mid]无解，在右半区间继续查找
        if(check(mid)){
            l=mid;
        }
        else{   //[mid,r]无解，在左半区间查找
            r = mid;
        }
    }
    printf("%.*lf", m, l);
    return 0;
}

问题 E: 求逆序对

题目描述

给定一个序列a1,a2,…,an，如果存在i<j并且ai>aj，那么我们称之为逆序对，求逆序对的数目。
注意：n<=105，ai<=105

输入

第一行为n,表示序列长度。
接下来的n行，第i+1行表示序列中的第i个数。

输出

所有逆序对总数。

样例输入

4

3

2

3

2

样例输出

3

题意：求出所给序列中包含的逆序对数量

思路：利用归并排序的特点，

并排序就是将一个序列分成两部分进行排序，然后将排序后的两个序列中的元素一个一个插入（如图）然后，我们发现，对于两个个正在排列的子序列，若后面的子序列中要插入元素，比如上图中要插入，则前面的子序列中剩下的待排序元素都可以与当前插入的元素组成逆序对（因为前面待排序的元素都比这个元素大，而且下标都比这个元素的下标要小），而且再次递归下去的子序列也是如此。

代码：


#include<iostream>
#include<algorithm>
#include<cstdio>
using namespace std;
typedef long long ll;
int a[100005], temp[100005];
ll cnt=0;        //测试点必须用long long 
void merge_sort(int l,int r){
    if(l>=r)
        return;
    int mid = (l + r) >> 1;
    merge_sort( l, mid);
    merge_sort( mid + 1, r);
    int p1 = l, p2 = mid + 1, p = l;
    while(p1<=mid&&p2<=r){
        if(a[p1]<=a[p2])
            temp[p++] = a[p1++];
        else
            temp[p++] = a[p2++],cnt+=mid-p1+1;    //所求答案
    }
    while(p1<=mid)
        temp[p++] = a[p1++];
    while(p2<=r)
        temp[p++] = a[p2++];
    for (int i = l; i <=r;i++){
        a[i] = temp[i];
    }
}
int main(){
    int n;
    cin >> n;
    for (int i = 1; i <= n;i++){
        cin >> a[i];
    }
    merge_sort( 1, n);
    cout << cnt;
}

问题 F: 剪绳子

题目描述

有N根绳子，第i根绳子长度为Li，现在需要M根等长的绳子，你可以对N根绳子进行任意裁剪（不能拼接），请你帮忙计算出这M根绳子最长的长度是多少。

输入

第一行包含2个正整数N、M，表示原始绳子的数量和需求绳子的数量。

第二行包含N个整数，其中第 i 个整数Li表示第 i 根绳子的长度。

已知：1≤N,M≤100000, 0<Li<109

输出

输出一个数字，表示裁剪后最长的长度，保留两位小数

样例输入

3 4

3 5 4

样例输出

2.50

提示第一根和第三根分别裁剪出一根2.50长度的绳子，第二根剪成2根2.50长度的绳子，刚好4根。

题意：把n根绳子剪成m根等长的绳子，求出每根绳子可得的最大长度

思路：实数二分，check函数用于计算可以得到多少根长度为mid的绳子，如果cnt>m就说明mid 还不是极限长度，还可以加长


#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int s[100005];
int n, m;
double check(double x){
    int cnt = 0;
    for (int i = 0; i < n;i++){
        cnt += s[i] / x;           //计算可以分为多少段
    }
    return cnt>= m;               //判断够不够分为m段
}
int main(){
    cin >> n >> m;
    for (int i = 0; i < n;i++){
        cin >> s[i];
    }
    double l = 0, r = 1e9;
    while((r-l)>1e-4){            //精度控制在1e-4
        double mid = (l + r) / 2;
        if(check(mid)){           //寻找极限长度
            l = mid;              //还不是最长，长度可以增加
        }
        else{
            r = mid;              //不够分为m跟，mid要缩小
        }    
    }
    printf("%.2f", r);
    return 0;
}

问题 G: 数列分段

题目描述

对于给定的一个长度为n的正整数数列，现要将其分成m段，并要求每段连续，且每段和的最大值最小。

例如，将数列4 2 4 5 1要分成3段：

若分为[4 2] [4 5] [1] ，各段的和分别为6 9 1，和的最大值为9；

若分为[4][2 4] [5 1] ，各段的和分别为4 6 6，和的最大值为6 ；

并且无论如何分段，最大值不会小于6。

所以可以得到要将数列4 2 4 5 1要分成3段，每段和的最大值最小为 6 。

输入

第 1 行包含两个正整数 n和m；

第 2 行包含 n个空格隔开的非负整数ai，含义如题目所述。

输出

仅包含一个正整数，即每段和最大值最小为多少。

样例输入

5 3

4 24 5 1

样例输出

6

提示

对于20% 的数据，有 n≤10；

对于40% 的数据，有 n≤1000；

对于100% 的数据，有n≤100000，m≤n，并且ai之和不超过 109

题意：将数列分成m段，求出最小的最大值

思路：设最优解为mid，如果每段和都小于mid则一定存在一种最优解段数不超过m否则就提高mid

代码：


#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int a[100005];
int n, m,l,r;
int check(int mid){
    int sum = 0, cnt = 0;
    for (int i = 0; i < n;i++){
        if(sum+a[i]<=mid)
            sum += a[i];
        else
            sum = a[i], cnt++;
    }
    return cnt >= m;
}
int main(){
    cin >> n >> m;
    int sum = 0,mx=0;
    for (int i = 0; i < n;i++){
        cin >> a[i];
        sum += a[i];
        if(mx<a[i])
            mx = a[i];
    }
    l = mx, r = sum;
    while(l<=r){
        int mid = (l + r) >> 1;
        if(check(mid)){
            l = mid + 1;
        }
        else{
            r = mid - 1;
        }
    }
    cout << l<<endl;
    return 0;
}

二进制枚举类

问题 E: 得到整数 X

题目描述

某君有n个互不相同的正整数，现在他要从这n个正整数之中无重复地选取任意个数，并仅通过加法凑出整数X。求某君有多少种不同的方案来凑出整数X。

输入

第一行，输入两个整数n,X(1≤n≤20,1≤X≤2000)。

接下来输入n个整数，每个整数不超过100。

输出

输出一个整数，表示能凑出X的方案数。

样例输入

6 6

1 2 3 4 5 6

样例输出

4

提示：

一共有 4 种方案：

1 5

1 2 3

2 4

思路：用二进制枚举，枚举所有子集，计算出和为x的子集数

代码：


#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int a[21];
int n, x, cnt = 0,sum = 0;
int main(){
    cin >> n >> x;
    for (int i = 0; i < n;i++){
        cin>>a[i];
    }
    for (int i = 0; i <(1<<n) ;i++){     //从0~2^n-1, 二进制上的0表示该位不取，1表示取 
        sum = 0;
        for (int j = 0; j < n;j++){      //判断第j位是否为1 
            if(i&(1<<j))
                sum+= a[j];
        }
        if(sum==x)
            cnt++;
    }
    cout << cnt << endl;
    return 0;
}

问题 G: islands 打炉石传说

题目描述

islands最近在完一款游戏“炉石传说”，又名“魔兽英雄传”。炉石传说是一款卡牌类对战的游戏。游戏是两人对战，总的来说，里面的卡牌分成两类，一类是法术牌，另一类是随从牌（所谓随从就是怪物）。

为了简化问题，现在假设随从牌的作用是召唤一个具有一定攻击力的怪物，法术牌的作用是给某个随从增加一定攻击力。随从牌和法术牌的使用都需要消耗一定的法力值。现在islands有10点法力值，手上有n张牌（islands最多有10张牌，否者他将会被爆牌T_T），有些是法术牌，有些是随从牌。islands现在是大劣势，他想要是利用这10点法力值使得召唤出来的所有随从的攻击力总和最高（法力值可以不用完）。

注意，任何法术牌都必须使用在某个召唤出来的随从上，也就是如果islands没有召唤过随从，他将不能使用任何法术牌。告诉islands他能召唤的随从的总攻击力最大是多少。

输入

每组数据首先输入一个n(0≤n≤10，表示islands有n张牌。

接下来n行，每行输入3个整数cost(0≤cost≤10)，d（0或者1），w(∣w∣≤1000)。

其中cost表示该牌的法力值消耗，如果d=0，表示该牌是攻击力为w的随从牌；如果d=1，表示是能给一个随从增加w攻击的法术牌。

输出

输出一行表示答案。

样例输入

1

1 0 100

样例输出

100

思路：枚举所有子集，就算每一个子集消耗的药水，总攻击力和是否有随从牌，如果消耗大于10或者没有出现随从牌则该次伤害不记录，最后求出合法数据中的最大值

代码：


#include<iostream>
#include<algorithm>
#include<cstdio>
#include<cmath>
using namespace std;
int data[10][3];
int main(){
    int n,Max = 0;
    cin >> n;
    for(int i=0;i<n;i++){
        cin >> data[i][0] >> data[i][1] >> data[i][2];
    }
    for(int i=0;i<(1<<n);i++){
        int cost = 0, sum = 0, flag = 0;    //记录药水消耗，总伤害，是否有随从牌
        for(int j=0;j<n;j++){
            if(i&(1<<j)){
                cost += data[j][0];
                sum += data[j][2];
                if(data[j][1]==0)          //有随从牌
                    flag = 1;
            }
        }
        if(flag==0)                        //没有随从牌跳过
            continue;        
        if(cost>10)                        //消耗大于10跳过
            continue;
        Max = max(Max, sum);
    }
    cout << Max;
    return 0;
}

问题 H: 幼儿园买玩具

题目描述

蒜厂幼儿园有n个小朋友，每个小朋友都有自己想玩的玩具。身为幼儿园园长的你决定给幼儿园买一批玩具，由于经费有限，你只能买m个玩具。已知玩具商店一共卖k种玩具，编号为1,2,3,...k，你让每个小朋友把想玩的玩具编号都写在了纸上。你希望满足尽可能多的小朋友的需求，请计算出最多能满足多少个小朋友的玩具需求

输入

第一行，输入三个整数n,m,k(1≤n≤100,1≤m≤k≤15)，中间用空格分开

接下来n行，第i+1(0≤i<n)行的第一个数字ai代表第i个小朋友想玩的玩具数量，

接下来有ai个数字，代表这ai个玩具的编号。

输出

输出一个整数，表示最多能满足多少小朋友的玩具需求。

样例输入

5 3 5

2 1 4

0

2 3 1

3 2 3 4

2 4 5

样例输出

3

思路：二进制枚举玩具的组合，检查该组合能够满足多少名小朋友的需求，最后输出最大值


#include<algorithm>
#include<iostream>
#include<cstdio>
#include<algorithm>
using namespace std;
const int NOI=1e2;
int ans;//记录答案
int a[1<<16];//定义二进制数组
int main(){
    int n,m,k;//n 个小朋友;只能买 m 个玩具;商店一共卖 k 种玩具
    cin>>n>>m>>k;
    for (int i=0,tp;i<n;i++){
        cin>>tp;
        if (tp!=0){
            for (int j=0,tmp;j<tp;j++){
                cin>>tmp;//第一个数字 a代表第 i 个小朋友想玩的玩具数量，
                a[i]|=(1<<(tmp-1));//用二进制来表达出某个娃子要的玩具
            }//接下来有 a个数字，代表这 a个玩具的编号。
        }
    }
    for (int i=0;i<(1<<k);i++){//二进制枚举子集
        int sum=0;//当前能满足的人的数量
        bool t=0;
        for (int j=0;j<k;j++){
            if (i&(1<<j)){//看选没选中
                sum++;
            }
            if (sum>m){
                t=1;
                break;
            }
        }
        if (t)continue;//判断钱够不够
        sum=0;
        for (int j=0;j<n;j++){
            if ((a[j]&i)==a[j]){//求出目前最多能满足多少小朋友的玩具需求
                sum++;
            }
        }
        ans=max(ans,sum);
    }
    cout<<ans<<endl;//输出答案
    return 0;
}

本文内容由网友自发贡献，转载请注明出处：https://www.wpsshop.cn/w/2023面试高手/article/detail/353600