算法|图论|BFS和DFS

图论|BFS和DFS

1.BFS
2.DFS

心有猛虎，细嗅蔷薇。你好朋友，这里是锅巴的C\C++学习笔记，常言道，不积跬步无以至千里，希望有朝一日我们积累的滴水可以击穿顽石。

BFS

BFS 广度优先搜索
BFS(Breadth-First-Search)，是一种遍历算法，也是很多重要的图的算法的原型(如：Dijstra单源最短路径算法和Prim最小生成树算法)。属于一种盲目搜寻法，目的是系统地展开并检查图中的所有节点，以找寻结果。
换句话说：它并不考虑结果的可能位置，彻底地搜索整张图，直到找到结果为止。
基本过程：BFS是从根节点开始，沿着树(图)的宽度遍历树(图)的节点。如果所有节点均被访问，则算法中止。一般用队列来辅助实现BFS算法。

迷宫寻路

题目描述

机器猫被困在一个矩形迷宫里。

迷宫可以视为一个 $n\times m$ 矩阵，每个位置要么是空地，要么是墙。机器猫只能从一个空地走到其上、下、左、右的空地。

机器猫初始时位于 $(1,1)$ 的位置，问能否走到 $(n,m)$ 位置。

输入格式

第一行，两个正整数 $n,m$。

接下来 $n$ 行，输入这个迷宫。每行输入一个长为 $m$ 的字符串，# 表示墙，. 表示空地。

输出格式

仅一行，一个字符串。如果机器猫能走到 $(n,m)$，则输出 Yes；否则输出 No。

样例 #1

样例输入 #1

3 5
.##.#
.#...
...#.
1
2
3
4

样例输出 #1

Yes
1

提示

样例解释

路线如下：$(1,1)\to (2,1)\to (3,1)\to (3,2)\to (3,3)\to (2,3)\to (2,4)\to (2,5)\to (3,5)$

数据规模与约定

对于 $100\%$ 的数据，保证 $1\le n,m\le 100$，且 $(1,1)$ 和 $(n,m)$ 均为空地。

实践代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
int dx[4]={1,-1,0,0};
int dy[4]={0,0,1,-1};//四个方向

char a[105][105];
bool vis[105][105]; //标记到达的点
struct node{
    int x,y;
};//记录坐标

void bfs(int n,int m){
    queue<node> q;
    q.push({1,1});
    vis[1][1] = true;
    while(!q.empty()){
        node tmp = q.front();
        q.pop();
        for(int i=0;i<4;i++){
            int tx,ty;
            tx=tmp.x+dx[i];
            ty=tmp.y+dy[i];
            if(tx<1||tx>n||ty<1||ty>m||a[tx][ty]=='#'||vis[tx][ty])
                continue;
            q.push({tx,ty});
            vis[tx][ty]=true;
        }
    }
}

void solve(){
    int n,m;cin>>n>>m;
    for(int i=1;i<=n;i++){
        for(int j=1;j<=m;j++){
            cin>>a[i][j];
        }
    }
    bfs(n,m);
    if(vis[n][m]) cout<<"YES"<<endl;
    else cout<<"NO"<<endl;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54

DFS

DFS 深度优先搜索
DFS(Depth-First-Search)，针对图和树的遍历算法。深度优先搜索是图论的经典算法，一般用堆或栈来辅助实现。
其过程简要来说：对每一个可能的分支路径深入到不能再深入为之，如果遇到死路就回退，回退过程中如果遇到未探索过的支路，就进入该支路继续深入，每个节点只能访问一次。

跳马问题

题目背景

在爱与愁的故事第一弹第三章出来前先练练四道基本的回溯/搜索题吧……

题目描述

中国象棋半张棋盘如图 $1$ 所示。马自左下角 $(0,0)$ 向右上角 $(m,n)$ 跳。规定只能往右跳，不准往左跳。比如图 $1$ 中所示为一种跳行路线，并将路径总数打印出来。

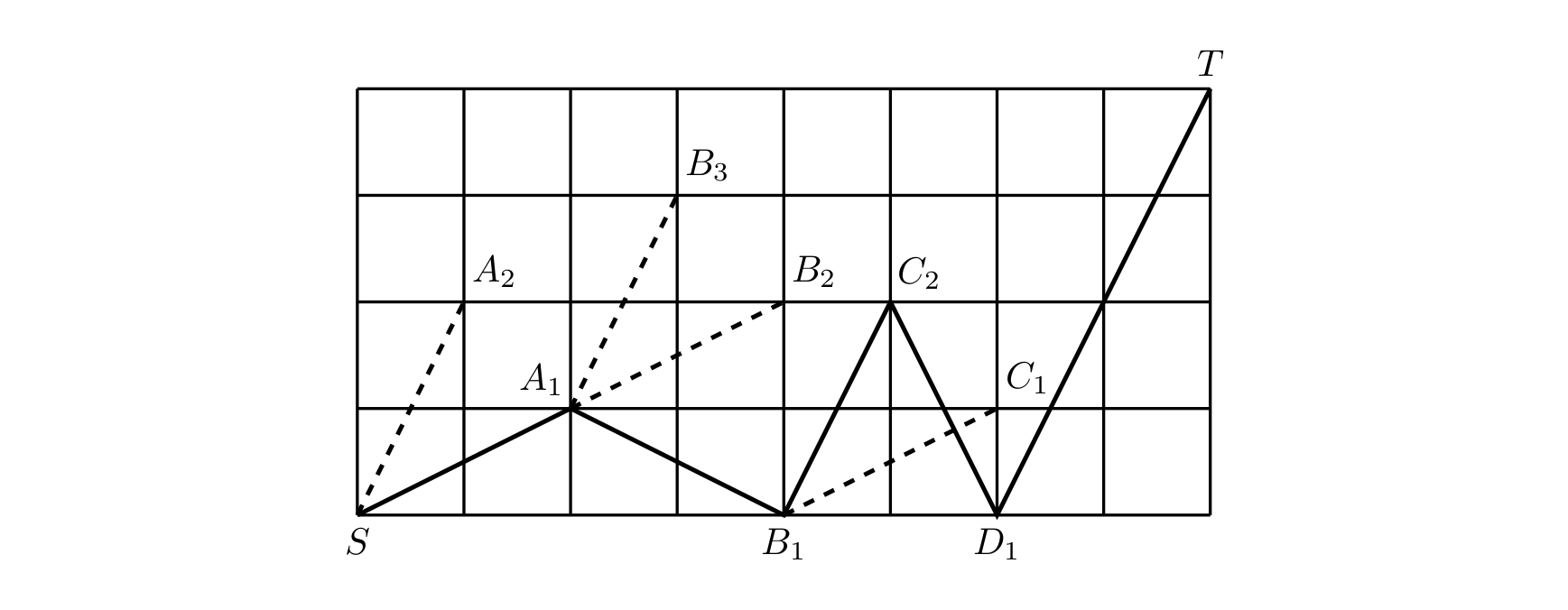
输入格式

只有一行：两个数 $n$，$m$。

输出格式

只有一个数：总方案数 $total$。

样例 #1

样例输入 #1

4 8
1

样例输出 #1

37
1

提示

对于 $100\%$ 的数据：$n,m\le 18$

实践代码：

#include<bits/stdc++.h>
using namespace std;
#define int long long
#define endl '\n'
//棋子的四种跳法
int dx[4]={1,2,2,1};//x轴移动
int dy[4]={2,1,-1,-2};//y轴移动

int dfs(int x,int y,int m,int n){
    if(x<0||x>m||y<0||y>n) return 0;//判断是否出界
    if(x==m&&y==n) return 1;//到达终点答案+1
    int sum=0;
    for(int i=0;i<4;i++){
        sum+=dfs(x+dx[i],y+dy[i],m,n);//递归四种情况
    }
    return sum;
}

void solve(){
    int n,m;cin>>n>>m;
    int ans = dfs(0,0,m,n);
    cout<<ans<<endl;
}
signed main(){
    ios::sync_with_stdio(false);
    cin.tie(0),cout.tie(0);
    int t=1;
    //cin>>t;
    while(t--){
        solve();
    }
    return 0;
}

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34

心有猛虎，细嗅蔷薇。再见了朋友~