小陈谈Java-用动图带你了解八大排序（一）_图解java八大排序csdn

目录

1.稳定性

2.插入排序

代码实现

代码分析

3.希尔排序

代码实现

算法分析

4.选择排序

5.堆排序

 代码分析

6.冒泡排序

---

很多同学学到排序就非常痛苦，那么今天这篇文章希望能解决同学们对于排序的迷惑，在排序之前，我们先了解一点，叫做排序的稳定性。

1.稳定性

我们在很多一系列数据中会出现相同的数据，那么排序的稳定性就是说，如果出现两个相同的数据（a1 & a2），排序之前a1在a2之前，那么如果排序之后a1还在a2之前，那么就称这个排序是一个稳定的排序，否则就是不稳定的排序。

---

那么在了解了什么事是排序的稳定性之后，我们就来看看第一种排序“插入排序”

2.插入排序

插入排序就类似于我们插扑克牌，找到比他小的就插进去，下面我们从这个动图来看看具体是怎么样的：

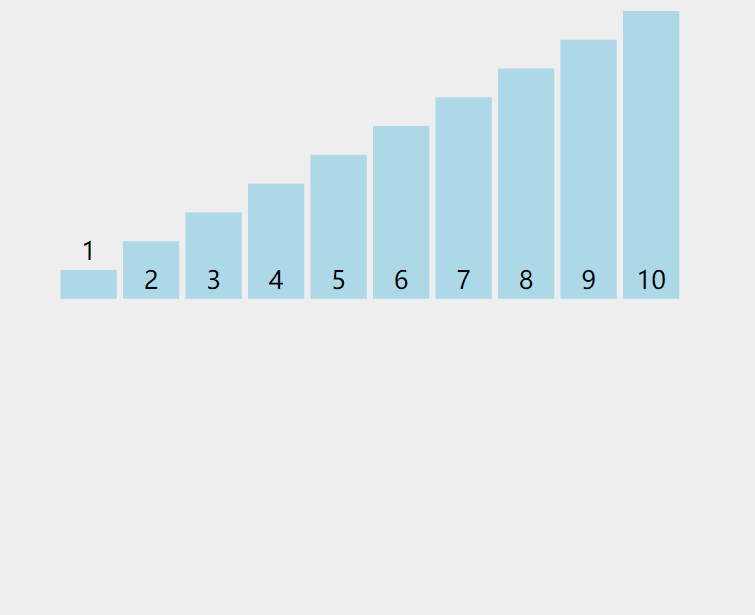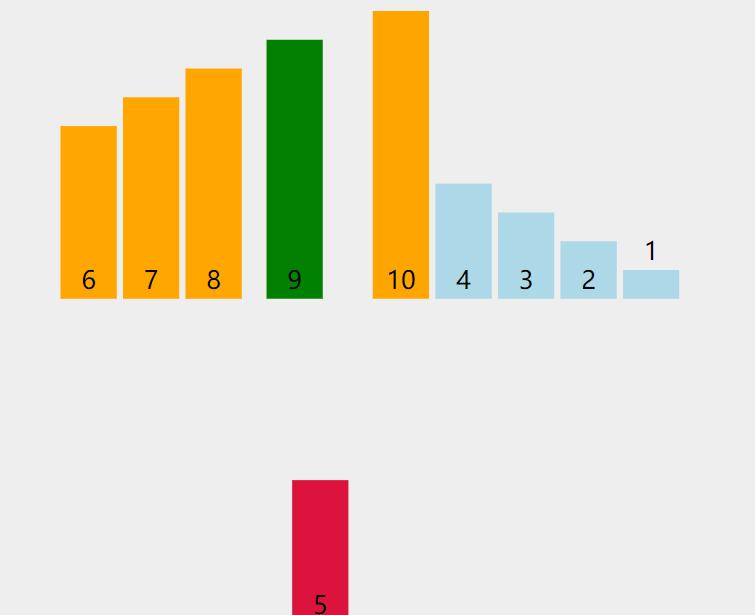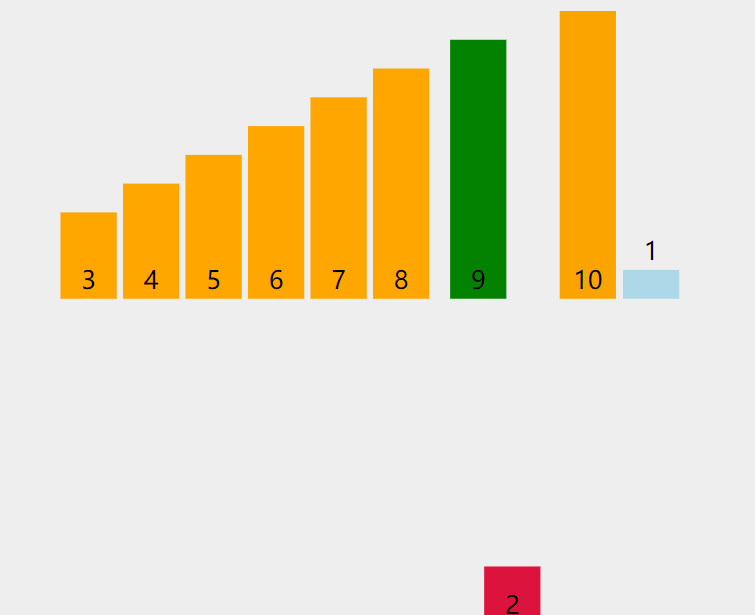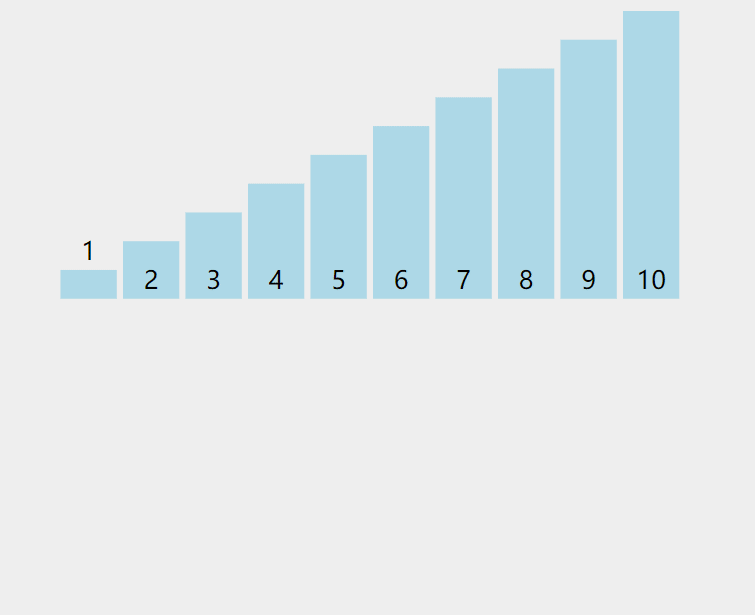
这张图很清晰的展示了插入排序的过程，那么怎么用代码来实现呢。

代码实现

首先我们先来看看代码的逻辑是怎么样的设想：

i和j指向数组的下标，j比i小1，如果j所在的元素小于i所在的元素，则将j+1与i交换，否则j一直后退至数组开始位置

代码实现：

public static void insertsort(int[] arr){
        int i=1;
        for(;i<arr.length;i++){
            //临时变量储存arr[i]的值，方便交换
            int tmp = arr[i];
            int j = i-1;
            for (; j >= 0 ; j--) {
                if(arr[j] > tmp) {
                    //让元素后移
                    arr[j+1] = arr[j];
                }else {
                    break;
                }
            }
            //交换比arr[i]大的最后一个元素
            arr[j+1] = tmp;
        }
        }

 那么这个就是插入排序的代码，那么我们可以想一想，这个代码的时间复杂度和空间复杂度又是多少呢

代码分析

在最好的情况下i和j分别只需要遍历一遍数组，所以时间复杂度是O(n)；当然如果数组是逆序那么时间复杂度就是O(n^2)。因为这个数组没有创建多余的变量所以空间复杂度是O(1)。

3.希尔排序

从上述所说的插入排序我们知道，插入排序的时间复杂度也有O(n^2),那么其实和冒泡排序没什么区别，而且元素集合越接近有序，直接插入排序算法的时间效率越高。那么希尔（Donald Shell）于1959年提出的一种排序算法——希尔排序通过分组的办法，降低排序的时间复杂度。就是通过分组，然后在组内进行插入排序的方式。

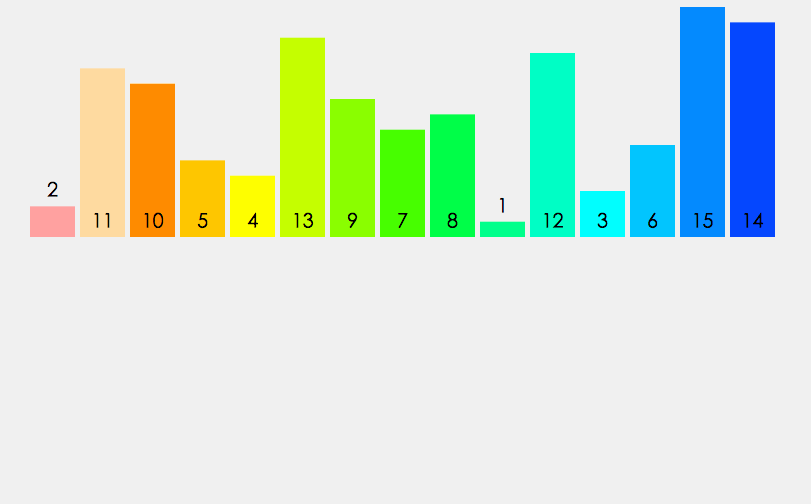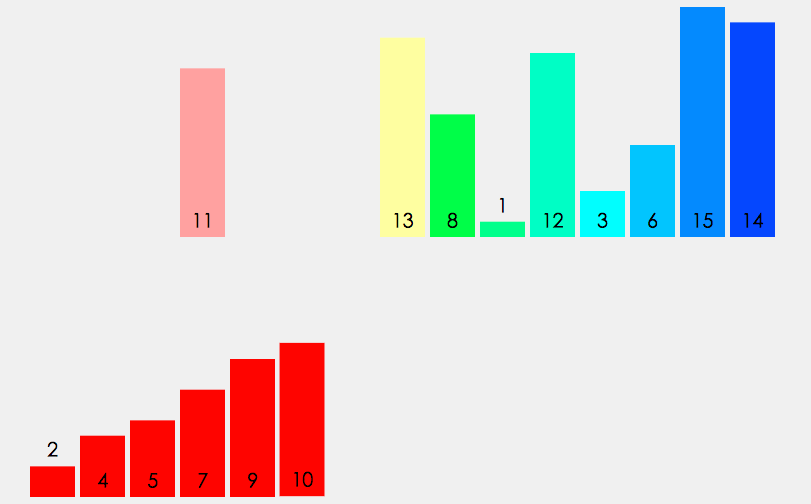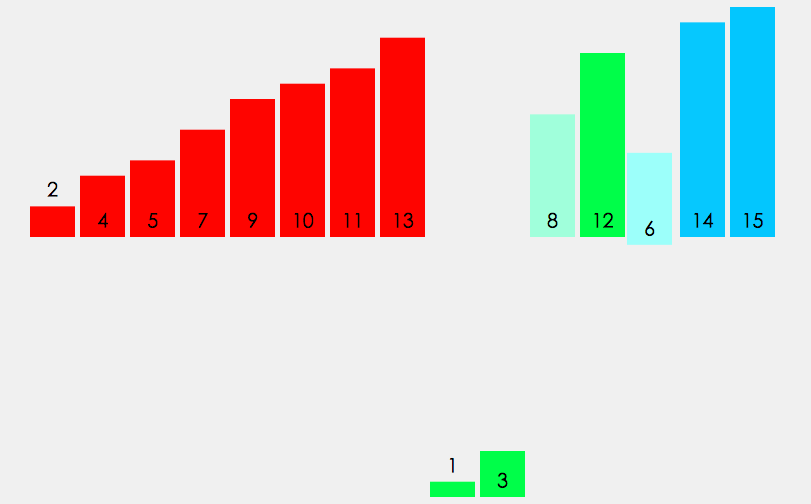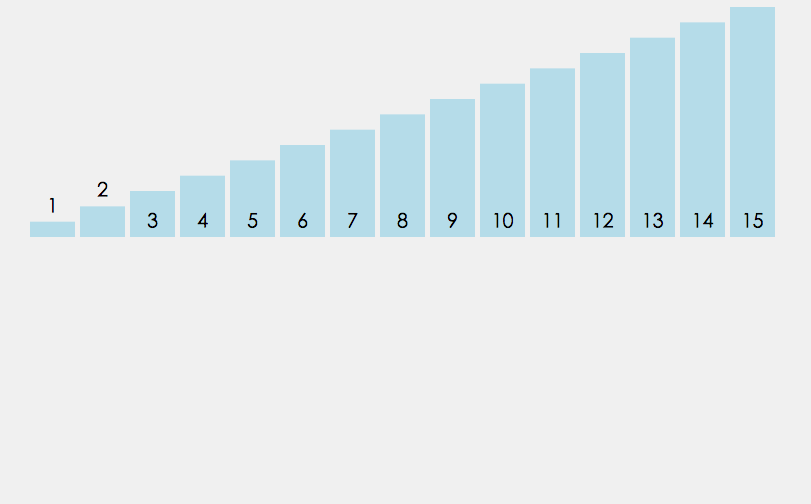
 那么主要的就是进行分组，当然这个分组的问题，至今都没有人可以给出一种完美的分组序列，我们就暂且按照数组长度的一半来分组，每次分组的长度又是上一次的一半。

代码实现

定义gap变量，然后每隔gap个单位的数字为一组，在组内进行直接插入排序

public static void shell_sort(int[]arr,int gap){
 
        for(int i=gap;i<arr.length;i++){
            int j=i-gap;
            int tmp=arr[i];
            for(;j>=0;j-=gap){
                if(arr[j] > tmp) {
                    arr[j+gap] = arr[j];
                }else {
                    break;
                }
            }
            arr[j+gap] = tmp;
        }
    }
//保持接口的统一性
    public static void shellsort(int[] arr){
        int gap=arr.length;
        while(gap>1){
            shell_sort(arr,gap);
            gap/=2;
        }
        shell_sort(arr,1);
    }

算法分析

希尔排序的分组情况比较复杂，至今都没有人准确的算出他的时间复杂度。根据一些书上的综合情况来看是O(n^1.25 ~1.6n^1.25)

稳定性：不稳定 

4.选择排序

上面所讲的两种排序都是插入排序，接下来我们了解一种选择排序。他的基本思想就是：

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完 。

 从这个动图我们也可以看到，每次都选择一个最小的然后进行交换。那么这个代码其实就很简单了。

public static void selectsort(int[] arr){
 
        for (int i = 0; i < arr.length; i++) {
            int minindex=i;
 
            for (int j = i+1; j < arr.length; j++) {
                if(arr[j] < arr[minindex]) minindex=j;
            }
 
                int temp=arr[i];
                arr[i]=arr[minindex];
                arr[minindex]=temp;
        }
 
    }

时间复杂度：O(N^2)

空间复杂度：O(1)

稳定性：不稳定

（代码简单就不做过多的解释啦）

5.堆排序

堆排序也是选择排序的一种，他是利用堆的性质来进行排序，这里注意到的是排升序要建大堆，排降序建小堆。

 代码分析

首先我们要先建一个堆，那么因为这里是要排升序，所以要建一个大根堆。

/**
     * 向下调整
     * @param root 要调整的数的根节点
     * @param len 数组的长度
     */
    public static void shiftDown(int[] arr,int root,int len){
        //找到子节点
        int child=root*2+1;
        while(child < len){
            //让child在左右子树较大的下面
            if((child+1)<len && arr[child]<arr[child+1]){
                child++;
            }
            if(arr[child]>arr[root]){
                //交换
                int temp=arr[child];
                arr[child]=arr[root];
                arr[root]=temp;
                root=child;
                child=root*2+1;
            }else{
                break;
            }
 
        }
    }
    public static void CreateHeap(int[] arr){
        for(int p=(arr.length-1-1)/2;p>=0;p--){
            shiftDown(arr,p,arr.length);
        }
    }
  

那么我们就建好了一个小根堆，那么接下来就来讨论下如何排序呢

从这张图我们可以看见每次排序都是从最后一个和0下标互换，然后再向下调整为一个大根堆，直到所有元素都排完，那么我们可以在排序的时候调用shiftDown ，来辅助排序。

public static void Heapsort(int[] arr){
        CreateHeap(arr);
        int end= arr.length-1;
        while(end>0){
            int temp=arr[0];
            arr[0]=arr[end];
            arr[end]=temp;
            shiftDown(arr,0,end);
            end--;
        }
    }

那么对于我们的堆排序来说：

1. 堆排序使用堆来选数，效率就高了很多。

2. 时间复杂度：O(N*logN)

3. 空间复杂度：O(1)

4. 稳定性：不稳定

6.冒泡排序

那么冒泡就是我们的老朋友啦，直接上代码：

 public static void bubbleSort(int[] array) {
        for (int i = 0; i < array.length-1; i++) {
            boolean flg = false;
            for (int j = 0; j < array.length-1-i; j++) {
                if(array[j] > array[j+1]) {
                    swap(array,j,j+1);
                    flg = true;
                }
            }
            if(!flg) {
                break;
            }
        }
    }

这个优化版的冒泡排序，比原来的冒泡排序就快很多啦

​​​​​​​