轨迹相似度整理_locality in-between polylines,lip python实现

0 度量测量

给定相似性测量f和三条轨迹Ti，Tj和Ta

• 如果f满足以下条件，那么称f为一个度量测量
  • 唯一性 
    • 
  • 非负性
    • 
  • 三角不等式
    • 
  • 对称性
    • 

一些聚类算法（K-means，KNN）、一些数据结构（KD树、ball-Tree）都需要在度量空间中实现

1 基于点之间的距离

1.1 最近对距离 Closest-Pair Distance

从两条轨迹中找到最近的一对点，并计算它们之间的距离

 1.2 点对距离和 Sum-of-Pairs Distance

设A,B为点数相同的两条轨迹，其距离定义如下:

1.3 欧几里得距离

•  优点：线性计算时间
• 缺点：轨迹长度必须一样

1.4 DTW

 DTW 笔记： Dynamic Time Warping 动态时间规整 （&DTW的python实现） 【DDTW，WDTW】_UQI-LIUWJ的博客-CSDN博客

• 缺点：对noise比较敏感 
  • 包括噪声在内的所有点都需要匹配

'Exact Indexing of Dynamic Time Warping'  VLDB 2002

1.4.1 DTW不是度量测量

 DTW 不满足的举例

• A=[1,1,1,2,2,2]
• B=[1,1,2,2]
• C=[2,2,2,1,1,1]

AB+BC=5 

AC=6

不满足三角不等式

1.5 LCSS 最长公共子序列

 文巾解题1143. 最长公共子序列_UQI-LIUWJ的博客-CSDN博客

• 优点：对noise不敏感
  • 在欧几里得距离和DTW距离中，所有的点都必须匹配，即使它们是离群点
  • LCSS允许跳过一些点，而不是重新排列它们
• 缺点：定义threshold比较困难（这里的threshold指的是，如果两点之间的距离小于这个threshold时，将被视为相同的一个点）

  DIscovering similar multidimensional trajectories, ICDE 2002

  • 
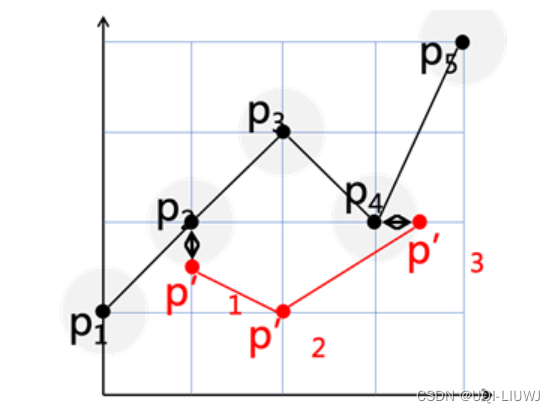
  • 比如上图，在这一对threshold的限制下，最长公共弄子序列的长度为2
• 另一个缺点是，它不区分具有相似公共子序列的轨迹（比如上上图，如果两个蓝色区域之间的白色区域长度差距很大，LCSS是不会察觉的）

1.5.1 LCSS 不是度量测量

LCSS 不满足三角不等式的例子

A：[1,2,3,4,5]

B：[3,4]

C：[1,2,3,4,5]

LCSS(A,C)=5，LCSS(A,B)=2，LCSS(B,C)=2

5≥2+2

 1.6  字符串编辑举例EDR

算法笔记：字符串编辑距离（Edit Distance on Real sequence，EDR）/ Levenshtein距离_UQI-LIUWJ的博客-CSDN博客

• 优点：
  • 对噪声不敏感
  • 比LCSS好。EDR会根据两个匹配子轨迹之间的间隙长度对其进行惩罚，这使得EDR比LCSS更精确
• 缺点：同LCSS，不好界定threshold 

''' Robust and fast similarity search formoving object trajectories' SigMod 2005

1.6.1 EDR 不是度量测量

EDR 不满足三角不等式的反例：

A=[0],B=[1,2],C=[2,3,3]，距离阈值为1

EDR(A,B)=1（0次替换，1次插入）

EDR(B,C)=1（0次替换，1次插入）

EDR(A,C)=3（1次替换，2次插入）

1.6.2 python 实现

import numpy as np
def EDR(TR1,TR2,eps):
    m,n = len(TR1)+1,len(TR2)+1
 
    matrix = np.zeros((m,n))
    #matrix[i][j]表示 TR1还剩i个元素，TR2还剩j个元素时，他们的编辑距离
 
    for i in range(1,m):
        matrix[i][0] = i 
    for j in range(1,n):
        matrix[0][j] = j
    #这两个for循环表示，一个轨迹没有元素了，另一个轨迹还有n个元素，那么此时编辑距离为n（插入/删除n个值
 
    for i in range(1,m):
        for j in range(1,n):
            #print(TR1[i-1],TR2[j-1])
            if np.linalg.norm(TR1[i-1]-TR2[j-1])<eps:
                cost = 0
            else:
                cost = 1
            #判断两个轨迹对应位置的值是否一致
            
            matrix[i][j]=min(matrix[i-1][j]+1,matrix[i][j-1]+1,matrix[i-1][j-1]+cost)
            #删除,插入，替换，这三个操作哪个编辑距离小一点，就选哪个
 
 
    return matrix
 
 
 
traj1=np.array([[12960834.80288441,  4845269.46493596],
        [12960722.25887924,  4845260.76402278],
        [12960622.85057397,  4845250.75798203],
        [12960572.31152516,  4845244.52233853],
        [12960519.880045  ,  4845238.86675827],
        [12960456.87321322,  4845233.93625503],
        [12960381.84387644,  4845232.63112222],
        [12960317.0559328 ,  4845230.45590127],
        [12960236.34930199,  4845214.93933889],
        [12960191.93282517,  4845209.13876105],
        [12960127.36752052,  4845202.03305778],
        [12960066.25312008,  4845200.14787205],
        [12960045.32505582,  4845201.30798631],
        [12959982.98614098,  4845196.81254434]])
traj2=np.array([[12960127.36752052,  4845202.03305778],
        [12960066.25312008,  4845200.14787205],
        [12960045.32505582,  4845201.30798631],
        [12959982.98614098,  4845196.81254434],
        [12959879.57033405,  4845196.37750167],
        [12959835.15385723,  4845186.51653973],
        [12959837.26892755,  4845187.24161012],
        [12959814.89370991,  4845183.18121657],
        [12959813.33523704,  4845183.03620255],
        [12959809.55037435,  4845182.31113246]])
 
disEDR=EDR(traj1,traj2,10)
disEDR[-1][-1],disEDR
'''
(14.0,
 array([[ 0.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 1.,  1.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 2.,  2.,  2.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 3.,  3.,  3.,  3.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 4.,  4.,  4.,  4.,  4.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 5.,  5.,  5.,  5.,  5.,  5.,  6.,  7.,  8.,  9., 10.],
        [ 6.,  6.,  6.,  6.,  6.,  6.,  6.,  7.,  8.,  9., 10.],
        [ 7.,  7.,  7.,  7.,  7.,  7.,  7.,  7.,  8.,  9., 10.],
        [ 8.,  8.,  8.,  8.,  8.,  8.,  8.,  8.,  8.,  9., 10.],
        [ 9.,  9.,  9.,  9.,  9.,  9.,  9.,  9.,  9.,  9., 10.],
        [10., 10., 10., 10., 10., 10., 10., 10., 10., 10., 10.],
        [11., 10., 11., 11., 11., 11., 11., 11., 11., 11., 11.],
        [12., 11., 10., 11., 12., 12., 12., 12., 12., 12., 12.],
        [13., 12., 11., 10., 11., 12., 13., 13., 13., 13., 13.],
        [14., 13., 12., 11., 10., 11., 12., 13., 14., 14., 14.]]))
'''
'
运行
运行

1.7 ERP（实数惩罚编辑距离）

• 上述基于编辑距离的测量方法（DTW\LCSS\EDR）都不是度量的
  • ——>索引、聚类、剪枝中往往用不了
• ERP 不需要阈值参数，而是设置一个参考点r进行测量
  • 

2 基于形状的距离

2.1 豪斯多夫距离

数学笔记/scipy 笔记：豪斯多夫距离（Hausdorff ）_python 豪斯多夫距离_UQI-LIUWJ的博客-CSDN博客

 

•  缺点：对噪声敏感

The computational geometry of comparing shapes, Efficient algorithms, 2009

2.2 Frechet距离

算法笔记：Frechet距离度量_UQI-LIUWJ的博客-CSDN博客

The computational geometry of comparing shapes, Efficient algorithms, 2009

2.3 上述方法对比

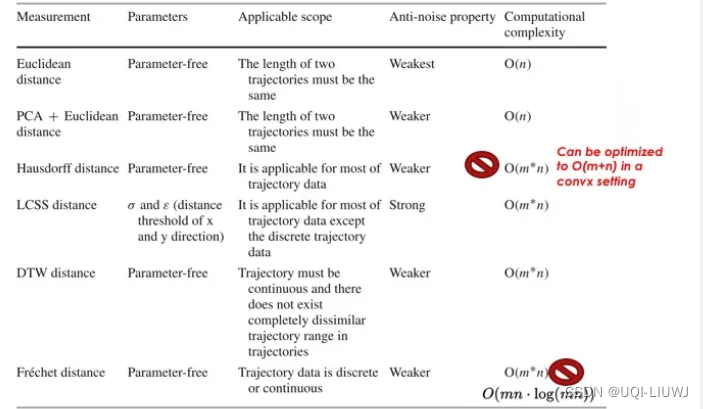
 3 基于片段的距离

3.1 One Way Distance

• 轨迹T1到T2的单边轨迹距离
  • T1中的点到T2的距离的积分结果，除以T1的距离
  • 
  • 
• 轨迹T1和T2的对称双边距离
  • 

  One way distance: for shape based similarity search of moving object trajectories, Geoinformatica 2008

3.2 多线位置距离（Locality In-between Polylines，LIP）

• 表示两个轨迹的第i个交点，
• 表示第i个交点和第i+1个交点之间所夹区域的面积

 

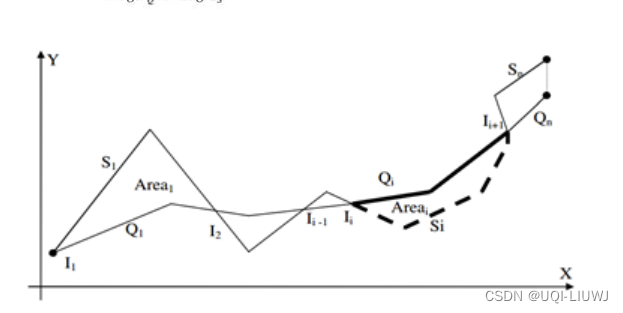
•   LIP方法很好理解，当某区域面积的周长占总长比重大时权重也自然就大；
  • 当Area均为0时，说明两条轨迹重合没有缝隙，LIP距离为0；
  • 当Area加权和大时，则说明两条轨迹之间缝隙较大，LIP距离也就大。
  • 此外，权重由区域周长占总长比重的大小而决定，也一定程度对抗了噪音点的干扰。

Similarity search in trajectory databases

3.3 EDwP